Introducción
Algunas cantidades pueden ser descritas totalmente por un número y una unidad; por ejemplo las magnitudes de superficie, volumen, masa, longitud y tiempo reciben el nombre de magnitudes escalares.
Por definición, una magnitud escalar es aquella que se define con sólo indicar su cantidad expresada en números y la unidad de medida.
Existe otra clase de magnitudes que para definirlas, además de la cantidad expresada en números y el nombre de la unidad de medida, se necesita indicar claramente la dirección y sentido en que actúan; estas magnitudes reciben el nombre de magnitudes vectoriales. Por ejemplo, cuando una persona visita la ciudad de Mérida, Yucatán, y nos pregunta cómo llegar al Puerto de Progreso, dependiendo de dónde se encuentre le diremos aproximadamente a qué distancia está y qué dirección seguir. Lo mismo sucede cuando se habla de la fuerza que se debe aplicar a un cuerpo, pues parte de señalar su valor se debe especificar si la fuerza se aplicará hacia arriba o hacia abajo, a la derecha o a la izquierda, hacia el frente o hacia atrás.
Una magnitud vectorial se define por su origen, magnitud, dirección y sentido. Consiste en un número, una unidad y una orientación angular.
Una magnitud vectorial puede ser representada gráficamente por medio de una flecha llamada vector, la cual es un segmento de recta dirigido. Para simbolizar una magnitud vectorial se traza una flechita horizontal sobre la letra que la define por ejemplo: 
Representación gráfica de un vector
Un vector tiene las siguientes características:
- Punto de aplicación u origen.
- Magnitud. Indica su valor y se representa por la longitud del vector de acuerdo con una escala convencional.
- Dirección. Señala la línea sobre la cual actúa, y puede ser horizontal, vertical u oblicua.
- Sentido. Indica hacia dónde va el vector, ya sea hacia arriba, abajo, a la derecha o a la izquierda , y queda señalado por la punta de la flecha.
Para representar un vector se necesita una escala convencional, la cual se establece de acuerdo con la magnitud del vector y el tamaño que se le desee dar; por ejemplo, si se desea representar en el pizarrón un vector fuerza de 400 N, con la dirección horizontal y el sentido positivo, se puede usar una escala de 1 cm igual a 100 N, para que al medir 4 cm, esté representado el vector de la siguiente manera:
- Escala: 1 cm = 100 N
(longitud del vector: 4 cm)
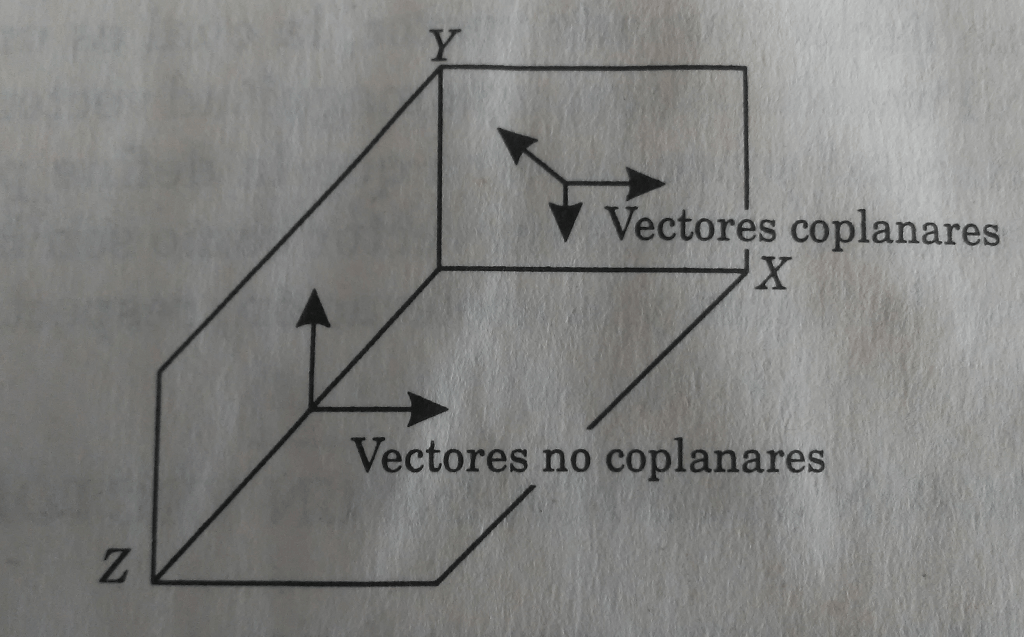
Vectores coplanares y no coplanares
Los vectores pueden clasificarse en coplanares, si se encuentran en el mismo plano o en dos ejes, y no coplanares, si están en diferente plano, es decir, en tres ejes.
Sistema de vectores colineales.
Se tiene un sistema de vectores colineales cuando dos o más vectores se encuentran en la misma dirección o línea de acción. Un vector colineal será positivo si su sentido es hacia la derecha o hacia arriba, y negativo si su sentido es hacia la izquierda o hacia abajo.
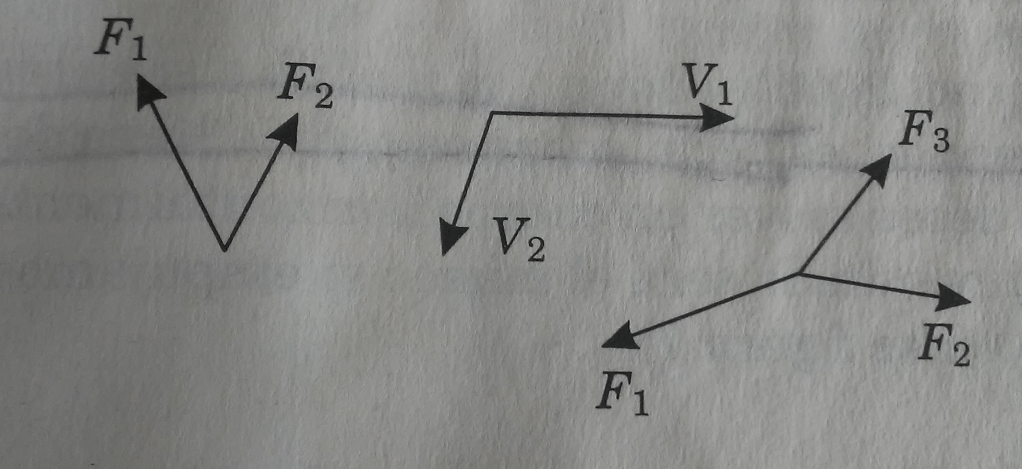
Sistemas de vectores concurrentes
Un sistema de vectores es concurrente cuando la dirección o línea de acción de los vectores se cruza en algún punto; el punto de cruce constituye el punto de aplicación de los vectores. A estos vectores se les llama angulares o concurrentes, porque forman un ángulo entre ellos.
Resultante y equilibrante de un sistema de vectores
La resultante de un sistema de vectores es el vector que produce el mismo efecto que los demás vectores del sistema. Por ellos, un vector resultante es aquel que es capaz de sustituir un sistema de vectores.
La equilibrante de un sistema de vectores, como su nombre lo indica, es el vector encargado de equilibrar el sistema. Por lo tanto, tiene la misma magnitud y dirección que la resultante, pero con sentido contrario.
Propiedades de los vectores
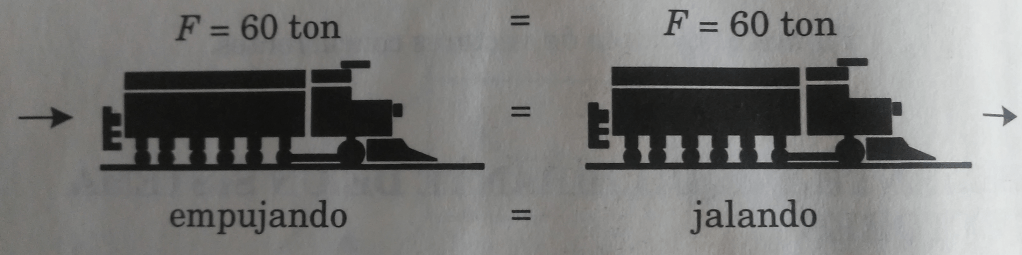
Propiedad de transmisiblidad del punto de aplicación
El efecto externo de un vector no se modifica si es trasladado en su misma dirección, es decir, sobre su propia línea de acción. Por ejemplo, si se desea mover un cuerpo horizontalmente, aplicando una fuerza, el resultado será el mismo si se empuja el cuerpo o si se jala.
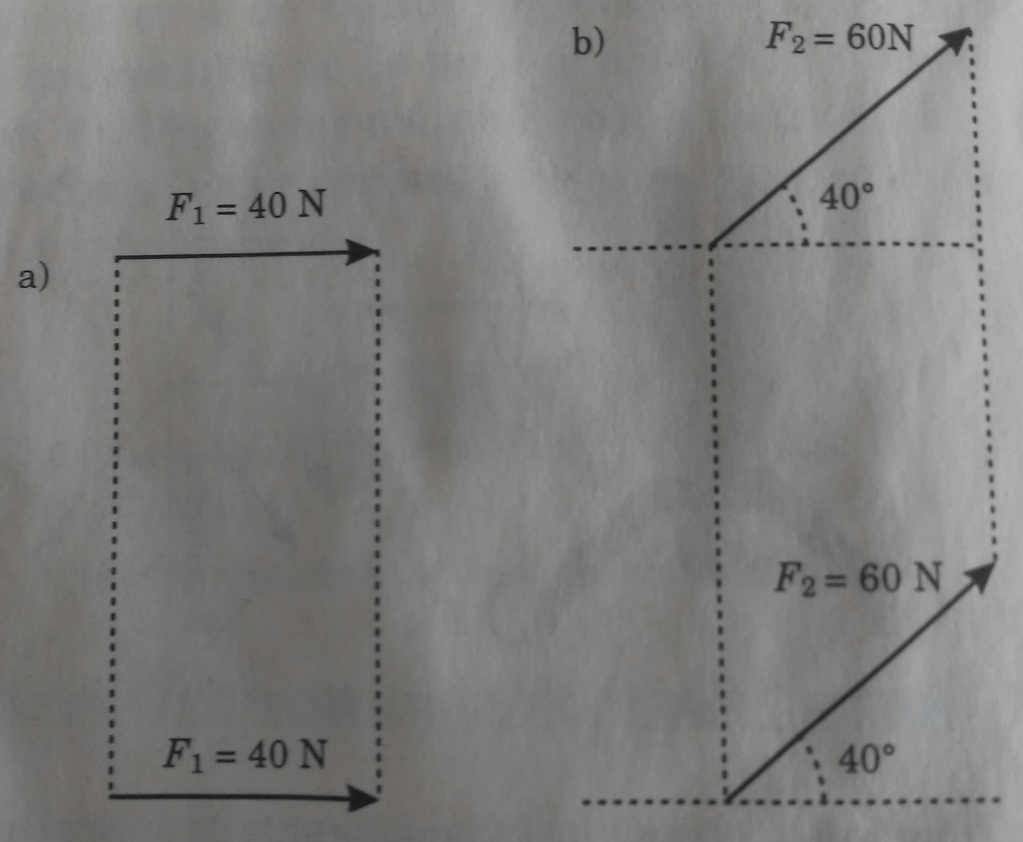
Propiedad de los vectores libres
Los vectores no se modifican si se trasladan paralelamente a si mismos. Esta propiedad se utilizará al sumar vectores por los métodos gráficos del paralelogramo, triángulo y polígono.
Dirección de un vector
La dirección de un vector puede darse con referencia a las direcciones convencionales de los puntos cardinales: norte, sur, este y oeste. Por ejemplo, los vectores 20 m oeste y 40 m a 30° al noreste, como se muestra en la figura.
Es importante hacer referencia a las líneas perpendiculares llamadas ejes. Estas líneas imaginarias suelen ser horizontal y vertical, pero podrían ser orientadas en otras direcciones siempre que las dos líneas sean perpendiculares. La línea imaginaria vertical se llama eje y. Las direcciones se dan mediante ángulos medidos en el sentido contrario al avance de las manecillas del reloj a partir de la posición del eje x positivo. Los vectores 40 m a 60° y 50 m a 210° se muestran en la siguiente figura.
Herramientas de cálculo 