Introducción
Se asumirá que la interconexión se realiza por medio de conductores eléctricos (alambres) con resistencia cero, esto es, conductores perfectos. Dado que los alambres no tienen resistencia, la energía en el circuito se concentra en cada elemento, por lo que se emplea el término de circuito de parámetros concentrados para describir la red. Como apoyo para este análisis, se tiene lo siguiente en la figura 1. El circuito muestra nodos, lazos y ramas.
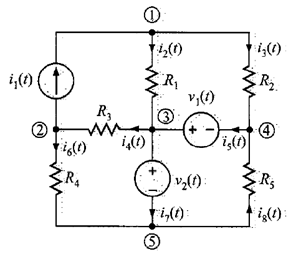
Un nodo es simplemente el punto de conexión de dos o más elementos de un circuito. Aunque un nodo puede extenderse con conductores perfectos, sigue siendo un solo nodo. En otras palabras, si a partir de algún punto del circuito se recorre un conductor perfecto hasta encontrar un elemento de circuito, la trayectoria total cubierta representa un nodo simple. Entonces, se puede asumir que un nodo es el extremo de un elemento de circuito junto con todos los conductores perfectos que estén conectados a él. Al examinar un circuito se observan diferentes trayectorias a través del mismo. Un lazo es simplemente cualquier trayectoria cerrada en el circuito en la cual ningún nodo aparece más de una vez. Por ejemplo, si se comienza en el nodo 1, un lazo podría contener los elementos ,
,
e
; otro lazo incluiría
,
,
,
e
; y así sucesivamente. Sin embargo, la trayectoria
,
,
,
,
e
no forma un lazo, ya que el nodo 3 aparece dos veces. Por último, una rama es una porción de circuito que contiene un sólo elemento, e incluye los nodos en los extremos de dicho elemento. El circuito de la figura 1 contiene 8 ramas.
Una vez establecidas estas definiciones, se considerarán las leyes de Kirchhoff, llamadas así por el científico alemán Gustav Robert Kirchhoff. La primera ley de Kirchhoff es la ley de Kirchhoff de corriente (LKC), que establece que la suma algebraica de las corrientes que entran en cualquier nodo es cero. En su forma matemática, esta ley se expresa como
donde es la j-ésima corriente que entra en el nodo a través de la rama
, y
es el número de ramas conectadas al nodo; esta fórmula se debe utilizarse cuando el circuito o red muestre fuentes de corriente o voltaje que dependan de la variable
.
También es posible aplicar esta fórmula
donde es la j-ésima corriente que entra en el nodo a través de la rama
, y
es el número de ramas conectadas al nodo; esta fórmula solo debe utilizarse cuando el circuito o la red presente fuentes de corriente o voltaje que tienen valores constantes.
Para entender el uso de esta ley, se considera un nodo como el que se muestra en la figura 2.

Si se desea escribir la ecuación de la LKC, se tiene que
Se supone que el signo algebraico de las corrientes que entran al nodo es negativo y, en consecuencia, que el signo de las corrientes de salida es positivo.
Que indica que la suma de las corrientes que entran a un nodo es igual a la suma de las corrientes que salen de él. Ambas expresiones en cursivas son formas alternativas de la ley de Kirchhoff de corriente.
Otro ejemplo sería el circuito de la figura 3.

Al aplicar la ley de Kirchhoff de corriente a este nodo se obtiene
De manera alternativa, la ecuación puede escribirse como
Al describir el resto de las ecuaciones de cada nodo en todo el circuito, se tiene lo siguiente
Problemas resueltos
Problema 1. La red de la figura 4 se representa por medio de un diagrama topológico. Calcular las corrientes desconocidas de la red.
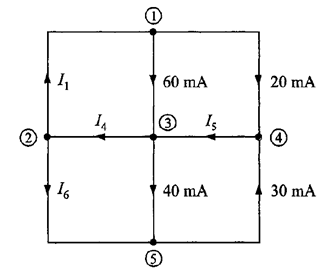
Solución. Suponiendo que las corrientes que salen del nodo son positivas, la ecuación de la LKC para el nodo 1 es
Para el nodo 2
Para el nodo 3
Para el nodo 4
Para el nodo 5
Las ecuaciones que se tienen son
En la primera ecuación, solo basta despejar . Entonces
En la quinta ecuación, se despeja
En la segunda ecuación, sustituyen los resultados de e
para despejar
De la cuarta ecuación, se despeja
Finalmente, los resultados de las corrientes desconocidas son ,
,
e
.
Problema 2. Se desea escribir las ecuaciones para LKC en el circuito de la figura 5.
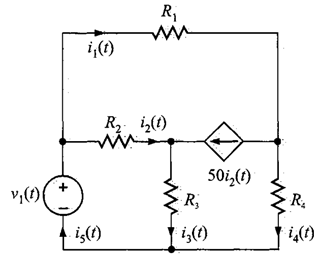
Solución. Aplicando la LKC para el nodo 1, se tiene la siguiente cuación
para el nodo 2,
para el nodo 3,
y para el nodo 4
Por lo tanto, las ecuaciones para los nodos 1 a 4 son
Aplicando la ley de Kirchhoff de corriente para superficies cerradas
Finalmente, se puede generalizar la ley de Kirchhoff de corriente para incluir una superficie cerrada. Por una superficie cerrada se entiende algún conjunto de elementos que están contenidos completamente en la superficie donde se encuentran interconectados. Ya que la carga que entra a cada elemento de la superficie es igual a la que sale del elemento (esto es, el elemento no almacena carga neta), se tiene que la corriente que entra a una interconexión es igual a la que sale de ella. Entonces, la ley de Kirchhoff de corriente también puede establecerse como la suma algebraica de las corrientes que entran en cualquier superficie cerrada es cero.
Problemas resueltos
Problema 1. Se quiere calcular e
en la red representada por el diagrama topológico de la figura 5.

Solución. Del diagrama se observa que en la superficie 1, al aplicar la LKC (suponiendo que las corrientes que salen de la superficie son positivas) se obtiene que
Y despejando
Al aplicar la LKC en la superficie 2
Problema 2. Encuentre e
en el circuito de la figura 6.
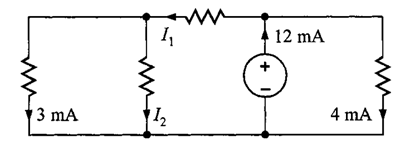
Solución. En el nodo 2, aplicando la LKC, se tiene que
Y en el nodo 1, aplicando el mismo procedimiento
Problema 3. Encontrar la corriente en el circuito de la figura 7.

Solución. Aplicando la LKC en el nodo principal, se tiene lo siguiente
Problema 4. Encontrar la corriente en el circuito de la figura 8.

Solución. En este caso se tiene un supernodo, por lo que, todo el análisis se basará en una sola aplicación a la LKC