División de voltaje para circuitos con fuentes y resistores (resistencias) múltiples. Circuitos eléctricos.

Introducción

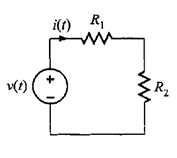
Se tiene un circuito como el de la figura 1. Se ha supuesto aquí que la corriente fluye en sentido de las manecillas del reloj (sentido horario) y la variable $i(t)$ se define en conformidad. Este supuesto puede o no ser correcto, dependiendo del valor de las diferentes fuentes de voltaje.

Figura 1. Circuito que ilustra resistores y fuentes múltiples para el análisis de división de voltaje.

Aplicando la ley de Kirchhoff de voltaje para este circuito, resulta que

$+v_{R_1} + v_2 (t) - v_3 (t) + v_{R_2} + v_4 (t) + v_5 (t) - v_1 (t) = 0$

Utilizando la ley de Ohm

$+R_1 i(t) + v_2 (t) - v_3 (t) + R_2 i(t) + v_4 (t) + v_5 (t) - v_1 (t) = 0$

$(R_1+R_2) i(t) = v_1 (t) - v_2 (t) + v_3 (t) - v_4 (t) - v_5 (t)$

$(R_1+R_2) i(t) = v(t)$

Por lo que, por medio de las definiciones anteriores, la figura 1 es equivalente a la figura 2. En otras palabras, la suma de varias fuentes de voltaje en serie puede reemplazarse con una fuente cuyo valor sea la suma algebraica de las fuentes individuales. Desde luego, este análisis puede generalizarse para un circuito con $N$ fuentes en serie.

Figura 2. Reducción del circuito equivalente de la figura 1.

Ahora, considerando un circuito con $N$ resistores en serie, como el de la figura 3, se aplica la LKV para obtener

$-v(t) + v_{R_1} + v_{R_2} + v_{R_3} + v_{R_4} + v_{R_5} + \cdots + v_{R_N} = 0$

$v(t) = v_{R_1} + v_{R_2} + v_{R_3} + v_{R_4} + v_{R_5} + \cdots + v_{R_N}$

Figura 3. Circuito en serie con N resistores.

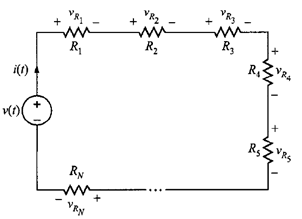
Aplicando la ley de Ohm

$v(t) = R_1 i(t) + R_2 i(t) + R_3 i(t) + R_4 i(t) + R_5 i(t) + \cdots + R_N i(t)$

$v(t) = (R_1 +R_2+R_3+R_4+R_5+ \cdots + R_N) i(t)$

$v(t) = R_S i(t)$

Esta última ecuación indica que la resistencia equivalente de $N$ resistores en serie es simplemente la suma de las resistencias individuales.

Figura 4. Reducción del circuito equivalente de la figura 3.

Por consiguiente

$\displaystyle i(t) = \frac{v(t)}{R_S}$

Problema resuelto

Problema 1. Dado el circuito de la figura 5, encuentre $I$ , $V_{bd}$ y la potencia que absorbe el resistor de 30 kΩ. Después, usar la división de voltaje para encontrar $V_{bc}$ .

Solución. Aplicando la LKV para la trayectoria abcdea

$(10 \ \text{k}) I + (20 \ \text{k}) I + 12 + (30 \ \text{k})I - 6 = 0$

$(60 \ \text{k})I = -6$

$I = -0.1 \ \text{mA}$

La magnitud de la corriente es de 0.1 mA y va en sentido antihorario (dirección contraria a las manecillas del reloj) a la supuesta.

El voltaje $V_bd$ puede calcularse usando las trayectorias cerradas $abdea$ o $bcdb$ . Las ecuaciones para ambos casos son

$(10 \ \text{k})I + V_{bd} + (30 \ \text{k})I - 6 = 0$

$(20 \ \text{k})I + 12 - V_{bd} = 0$

Tomando cualquiera de las dos ecuaciones mencionadas, se obtiene que $V_{bd} = 10 \ \text{V}$ .

Por último, la potencia que absorbe el resistor de 30 kΩ es

$P = V \cdot I$

$P = I^2 \cdot R = {(-0.1 \times 10^{-3})}^2 (30 \times 10^3)$

$P = 0.3 \ \text{mW}$

Para determinar el voltaje $V_{bc}$ , se requiere sumar por una parte las fuentes y por otra los resistores restantes, dado que ambos tipos de elementos están en serie, y reducir la red a la que se muestra en la figura 6.

Figura 6. Reducción del circuito de la figura 5.

Entonces,

$\displaystyle V_{bc} = \left(\frac{20 \ \text{k}}{20 \ \text{k} + 40 \ \text{k}} \right) (-6) = \left(\frac{20 \times 10^3}{20 \times 10^3 + 40 \times 10^3} \right) (-6)$

$\therefore V_{bc} = -2 \ \text{V}$

División de voltaje para circuitos con fuentes y resistores (resistencias) múltiples. Circuitos eléctricos.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

División de voltaje para circuitos con fuentes y resistores (resistencias) múltiples. Circuitos eléctricos.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta