Combinaciones de resistores en serie y en paralelo. Circuitos eléctricos.

Introducción

La resistencia equivalente de N resistores en serie es

$R_S=R_1+R_2+ \cdots +R_N$

Y la resistencia equivalente de $N$ resistores en paralelo es

$\displaystyle \frac{1}{R_P} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_N}$

Problemas resueltos

Problema 1. Para la red de la figura 1, se desea determinar la resistencia en las terminales A-B.

Solución. Analizando de derecha a izquierda, se observa que hay una suma en serie en las resistencias de 1 kΩ y 2 kΩ, cuyo resultado es 3 kΩ .

$\displaystyle R_{S1} = R_{1\text{k} \Omega-2 \text{k} \Omega} = 1\ \text{k} \Omega + 2 \ \text{k} \Omega$

$\displaystyle R_{S1} = 3 \ \text{k} \Omega$

Al reducir el circuito, se tiene la resistencia de 6 kΩ y 3 kΩ en paralelo, cuyo equivalente es de 2 kΩ

$\displaystyle \frac{1}{R_{P1}} = \frac{1}{R_{6\text{k} \Omega || S1}} = \frac{1}{R_{S1}} + \frac{1}{R_{6\text{k}\Omega}} = \frac{1}{3 \text{k}\Omega} + \frac{1}{6 \text{k}\Omega}$

$R_{P1} = 2 \ \text{k} \Omega$

Sumando la resistencia en serie de 10 kΩ y 2 kΩ se tiene 12 kΩ

$R_{S2} = 10 \ \text{k} \Omega + R_{P1} = 10 \ \text{k} \Omega + 2 \ \text{k} \Omega$

$R_{S2} = 12 \ \text{k} \Omega$

Esta primera parte reducida se muestra en la figura 2.

Figura 2. Primera reducción del circuito de la figura 1.

Después, se tiene la resistencia equivalente en paralelo en los resistores de 12 kΩ y 6 kΩ, cuyo resultado es 4 kΩ.

$\displaystyle \frac{1}{R_{P2}} = \frac{1}{6 \ \text{k} \Omega} + \frac{1}{R_{S2}} = \frac{1}{6 \ \text{k} \Omega} + \frac{1}{12 \ \text{k} \Omega}$

$\displaystyle R_{P2} = 4 \ \text{k} \Omega$

Se tiene otra parte de resistencia en serie en los resistores 2 kΩ y 4 kΩ, dando como resultado 6 kΩ.

$\displaystyle R_{S3} = 2 \ \text{k} \Omega + R_{P2} = 2 \ \text{k} \Omega + 4 \ \text{k} \Omega$

$\displaystyle R_{S3} = 6 \ \text{k} \Omega$

La segunda parte de reducida de la red se muestra en la figura 3.

Figura 3. Segunda reducción del circuito de la figura 1.

Luego, se tiene resistencia equivalente en paralelo en 6 kΩ y 6 kΩ, dando como resultado de 3 kΩ.

$\displaystyle \frac{1}{R_{P3}} = \frac{1}{6 \ \text{k} \Omega} + \frac{1}{R_{S3}} = \frac{1}{6 \ \text{k} \Omega} + \frac{1}{6 \ \text{k} \Omega}$

$\displaystyle R_{P3} = 3 \ \text{k} \Omega$

Sumando la resistencia equivalente en serie mediante los resistores 3 kΩ y 9 kΩ, da como resultado de 12 kΩ

$\displaystyle R_{S4} = 9 \ \text{k} \Omega + R_{P3} = 9 \ \text{k} \Omega + 3 \ \text{k} \Omega$

$\displaystyle R_{S4} = 12 \ \text{k} \Omega$

La tercera parte reducida de la red se muestra en la figura 4.

Figura 4. Tercera reducción del circuito de la figura 1.

Por último, se tiene en paralelo con los resistores de 12 kΩ y 4 kΩ, obteniendo 3 kΩ.

$\displaystyle \frac{1}{R_{P4}} = \frac{1}{4 \ \text{k} \Omega} + \frac{1}{R_{S4}} = \frac{1}{4 \ \text{k} \Omega} + \frac{1}{12 \ \text{k} \Omega}$

$\displaystyle R_{P4} = 3 \ \text{k} \Omega$

La cuarta parte reducida de la red se muestra en la figura 5.

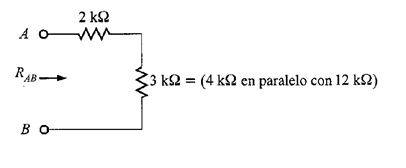
Figura 5. Cuarta reducción del circuito de la figura 1.

Finalmente, se tiene la resistencia equivalente en serie en los resistores 2 kΩ y 3 kΩ, quedando un resultado de 5 kΩ. Se concluye que la resistencia en las terminales A-B es

$\displaystyle R_{AB} = R_S$