Circuitos con combinaciones de resistores en serie y en paralelo. Circuitos eléctricos.

Problemas resueltos

Problema 1. Se desea encontrar todas las corriente y voltajes marcados en la red de escalera de la figura 1.

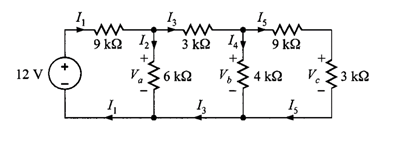
Solución. El análisis comenzará en el extremo derecho del circuito, combinando los resistores para determinar la resistencia total vista por la fuente de 12 V. Esto ayudará a calcular la corriente $I_1$ . Después podrán calcularse todas las corrientes y voltajes de la red aplicando las leyes de Ohm, LKV y LKC o división de voltaje y corrientes.

En el extremo derecho del circuito, los resistores de 9 kΩ y 3 kΩ están en serie, por lo que se pueden combinar en un resistor equivalente de 12 kΩ.

$\displaystyle R_{S1} = 9 \ \text{k} \Omega + 3 \ \text{k} \Omega$

$\displaystyle R_{S1} = 12 \ \text{k} \Omega$

Este resistor está es paralelo con el de 4 kΩ, y su combinación produce un resistor equivalente de 3 kΩ.

$\displaystyle \frac{1}{R_{P1}} = \frac{1}{4 \ \text{k} \Omega} + \frac{1}{R_{S1}} = \frac{1}{4 \ \text{k} \Omega} + \frac{1}{12 \ \text{k} \Omega}$

$\displaystyle R_{P1} =3 \ \text{k} \Omega$

La primera parte del extremo derecho del circuito se ilustra en la figura 2.

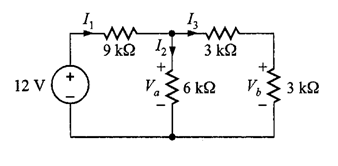
Figura 2. Primera parte del circuito reducido de la figura 1.

En esta figura, los dos resistores de 3 kΩ están en serie,

$\displaystyle R_{S2} = 3 \ \text{k} \Omega + R_{P1} = 3 \ \text{k} \Omega + 3 \ \text{k} \Omega$

$\displaystyle R_{S2} = 6 \ \text{k} \Omega$

y su combinación está en paralelo con el resistor de 6 kΩ

$\displaystyle \frac{1}{R_{P2}} = \frac{1}{6 \ \text{k} \Omega} + \frac{1}{R_{S2}} = \frac{1}{6 \ \text{k} \Omega} + \frac{1}{6 \ \text{k} \Omega}$

$\displaystyle R_{P2} = 3 \ \text{k} \Omega$

Al combinar estas tres resistencias se llega al circuito de la figura 3.

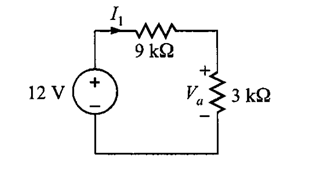
Figura 3. Última reducción del circuito de la figura 1.

Al aplicar la ley de Kirchhoff de voltaje al circuito de la figura 3 se obtiene

$\displaystyle \sum_{j=1}^{N}{V_j} = 0$

$(9 \ \text{k}) I_1 + (3 \ \text{k}) I_1 - 12 = 0$

$(9 \ \text{k} + 3 \ \text{k}) I_1 = 12$

$\therefore I_1 = 1 \ \text{mA}$

$V_a$ puede calcularse con la ley de Ohm o usando la ley de Kirchhoff de voltaje,

Una vez que se conocen los valores de $I_1$ y $V_a$ , es posible determinar todas las corrientes y voltajes de la figura 2. Dado que $V_a = 3 \ \text{V,}$ la corriente $I_2$ puede calcularse con la ley de Ohm

$V_a = (6 \ \text{k}) I_2$

$\displaystyle I_2 = \frac{V_a}{6 \ \text{k}}$

$\displaystyle I_2 = \frac{3}{6 \times 10^3} = \frac{1}{2} \times 10^{-3}$

$\displaystyle \therefore I_2 = \frac{1}{2} \ \text{mA} = 0.5 \ \text{mA}$

Para obtener $I_3$ , puede calcularse utilizando la ley de Kirchhoff de corriente o con la ley de Ohm

\displaystyle V_a = (3 \ \text{k} + 3 \ \text{k}) I_3

Es posible calcular $V_b$ al aplicar la ley de Kirchhoff de voltaje al lazo de la derecha de la figura 2, o también, se puede usar la ley de Ohm, dado que $V_b$ es igual a la caída de voltaje en el resistor de 3 kΩ.

Ahora ya es posible calcular las corrientes y voltajes desconocidos finales de la figura 1. Al conocer $V_b$ se puede calcular $I_4$ usando la ley de Ohm

$V_b = (4 \ \text{k}) I_4$

$\displaystyle I_4 = \frac{V_b}{4 \ \text{k}}$

$\displaystyle I_4 = \frac{1.5}{4 \times 10^3} = 0.375 \times 10^{-3}$

$\displaystyle \therefore I_4=0.375 \ \text{mA} = \frac{3}{8} \ \text{mA}$

Así, $I_5$ puede calcularse a partir de la ley de Kirchhoff de corriente o usando la regla de la división de corriente

\displaystyle I_5 = \left[\frac{4 \ \text{k}}{4 \ \text{k} + (9\ \text{k} + 3 \ \text{k})} \right] I_3

Finalmente, $V_c$ se calcula por medio de la ley de Ohm (ya que $I_5$ circula a través del resistor de 3 kΩ) o usando la división de voltaje (esto es, el voltaje $V_b$ se divide entre los resistores de 9 kΩ y de 3 kΩ, por la figura 1). Entonces,

\displaystyle V_c = \left(\frac{3 \ \text{k}}{3 \ \text{k} + 9 \ \text{k}} \right) V_b

En la figura 4 se muestra el circuito con los cálculos obtenidos de cada corriente y voltaje.

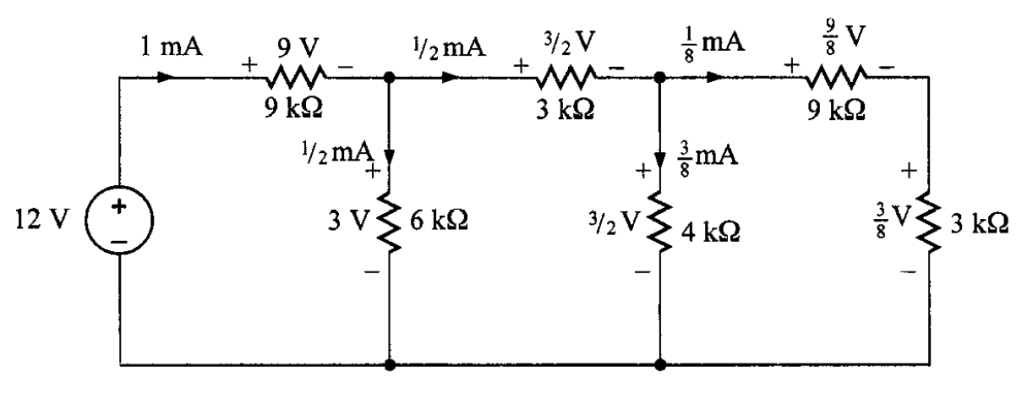
Figura 4. Circuito de la figura 1 señalando los voltajes y las corrientes calculadas.

Problema 2. Dado el circuito de la figura 5, con $\displaystyle I_4 = \frac{1}{2} \ \text{mA}$ , encuentre el voltaje de la fuente $V_o$ .

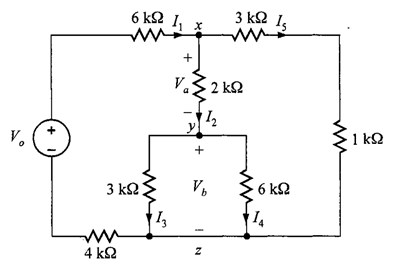
Solución. Por la ley de Ohm, se determina $V_b$

$V_b=(6 k) I_4$

$V_b=(6 \ \text{k})(0.5 \ \text{m})$

$V_b=(6 \times 10^3 )(0.5 \times 10^{-3})=3$

$V_b=3 \ \text{V}$

Calculando $I_3$

$V_b=(3 \ \text{k}) I_3$

$\displaystyle I_3 = \frac{V_b}{3k}$

$\displaystyle I_3 = \frac{3}{3k} = \frac{3}{3 \times 10^3} = 1 \times 10^{-3}$

$I_3 = 1 \ \text{mA}$

Al aplicar la ley de Kirchhoff en el nodo y se obtiene

$\displaystyle \sum_{j=1}^{N}{I_j} = 0$

$-I_2+I_3+I_4=0$

$I_2=I_3+I_4$

$\displaystyle I_2 = 1 \ \text{m} + 0.5 \ \text{m}$

$\displaystyle I_2 = 1 \times 10^{-3} + 0.5 \times 10^{-3} = 1.5 \times 10^{-3}$

$I_2=1.5 \ \text{mA}$

Entonces, por la ley de Ohm se tiene

$V_a = (2\ \text{k}) I_2$

$V_a = (2\ \text{k}) (1.5 \ \text{m})$

$V_a = (2 \times 10^3 )(1.5 \times 10^{-3}) = 3$

$V_a=3 \ \text{V}$

Ahora se puede calcular $I_5$ , dado que se conoce $V_a+V_b$

$\displaystyle I_5 = \frac{V_a+V_b}{3 \ \text{k} + 1 \ \text{k}}$

$\displaystyle I_5 = \frac{3+3}{4 \ \text{k}}$

$\displaystyle I_5 = \frac{3+3}{4 \times 10^{3}} = 1.5 \times 10^{-3}$

$I_5=1.5 \ \text{mA}$

Al aplicar la ley de Kirchhoff en el nodo x se obtiene

$-I_1+I_2+I_5=0$

$I_1=I_2+I_5$

$I_1=1.5 \ \text{m} + 1.5 \ \text{m}$

$I_1 = 1.5 \times 10^{-3} + 1.5 \times 10^{-3} = 3 \times 10^{-3}$

$I_1 = 3 \ \text{mA}$

Si se aplica la LKV a cualquier trayectoria cerrada que contenga a $V_o$ se puede conocer el valor de su fuente de entrada. Por ejemplo, si la trayectoria es el lazo externo, por la LKV se obtiene

$\displaystyle (6 \ \text{k}) I_1 + (3 \ \text{k}) I_5 + (1 \ \text{k}) I_5 + (4 \ \text{k}) I_1 - V_o = 0$

$V_o = (10 \ \text{k}) I_1 + (4 \ \text{k}) I_5$

$V_o = (10 \ \text{k})(3 \ \text{m}) + (4 \ \text{k})(1.5 \ \text{m})$

$V_o = (10 \times 10^3)(3 \times 10^{-3}) + (4 \times 10^3)(1.5 \times 10^{-3}) = 30 + 6$

$\therefore V_o=36 \ \text{V}$

Si se hubiera seleccionado la trayectoria que contiene a la fuente y los puntos $x$ , $y$ y $z$ , se habría obtenido

$(6 \ \text{k}) I_1 + V_a + V_b + (4 \ \text{k}) I_1 - V_o = 0$

$V_o = (10 \ \text{k}) I_1 + V_a + V_b$

$V_o = (10 \ \text{k})(3 \ \text{m}) + 3 + 3$

$V_o = (10 \times 10^3)(3 \times 10^{-3}) + 3 + 3 = 30 + 3 + 3$

$\therefore V_ o = 36 \ \text{V}$

Ley de Ohm	Ley de Kirchhoff de voltaje (LKV)
$V_a = (3 \ \text{k}) I_1$	$\displaystyle \sum_{j=1}^{N}{V_j} = 0$
$V_a = (3 \ \text{k})(1 \ \text{m})$	$(9 \ \text{k}) I_1 + V_a - 12 = 0$
$V_a = (3 \times 10^3)(1 \times 10^{-3})$	$V_a = 12 - (9 \ \text{k}) I_1$
$\therefore \therefore V_a = 3 \ \text{V}$	$V_a = 12-(9 \ \text{k})(1 \ \text{m})$
	$V_a = 12 - (9 \times 10^3 )(1 \times 10^{-3}) = 12 - 9$
	$V_a = 3 \ \text{V}$

Utilizando LKC	Utilizando ley de Ohm
$\displaystyle \sum_{j=1}^{N}{I_j} = 0$	$\displaystyle V_a = (3 \ \text{k} + 3 \ \text{k}) I_3$
$\displaystyle -I_1+I_2+I_3=0$	$\displaystyle V_a = (6 \ \text{k}) I_3$
$\displaystyle I_3=I_1-I_2$	$\displaystyle I_3 = \frac{3}{6 \ \text{k}}$
$\displaystyle I_3=1 \ \text{m} - 0.5 \ \text{m}$	$\displaystyle I_3 = \frac{3}{6 \times 10^3} = \frac{1}{2} \times 10^{-3}$
$\displaystyle I_3 = 1\times 10^{-3} - 0.5 \times 10^{-3} = 0.5 \times 10^{-3} \ \text{A}$	$\displaystyle \therefore I_3 = \frac{1}{2} \ \text{mA} = 0.5 \ \text{mA}$
$\displaystyle \therefore I_3 = 0.5 \ \text{mA} = \frac{1}{2} \ \text{mA}$

Utilizando LKV	Utilizando ley de Ohm
$\displaystyle \sum_{j=1}^{N}{V_j} = 0$	$V_b = (3 \ \text{k}) I_3$
$(3 \ \text{k}) I_3 + V_b - V_a = 0$	$V_b = (3 \ \text{k})(0.5 \ \text{m}) = (3 \times 10^3)(0.5 \times 10^{-3})$
$V_b = V_a - (3\ \text{k}) I_3$	$\displaystyle \therefore V_b = 1.5 \ \text{V} = \frac{3}{2} \ \text{V}$
$V_b = 3 - (3 \ \text{k})(0.5 \ \text{m})$
$V_b = 3 - (3 \times 10^3)(0.5 \times 10^{-3}) = 3 - 1.5$
$\displaystyle \therefore V_b = 1.5 \ \text{V} = \frac{3}{2} \ \text{V}$

Utilizando LKC	Utilizando división de corriente
$\displaystyle \sum_{j=1}^{N}{I_j} = 0$	$\displaystyle I_5 = \left[\frac{4 \ \text{k}}{4 \ \text{k} + (9\ \text{k} + 3 \ \text{k})} \right] I_3$
$-I_3+I_4+I_5=0$	$\displaystyle I_5 = \left(\frac{4 \ \text{k}}{4 \ \text{k} + 12 \ \text{k}} \right)(0.5 \ \text{m})$
$I_5 = I_3 - I_4$	$\displaystyle I_5 = \left(\frac{4 \times 10^3}{4 \times 10^3 + 12 \times 10^3} \right)(0.5 \times 10^{-3}) = 0.125 \times 10^{-3}$
$I_5 = 0.5 \ \text{m} + 0.375 \ \text{m}$	$\displaystyle \therefore I_5=0.125 \ \text{mA} = \frac{1}{8} \ \text{mA}$
$I_5 = 0.5 \times 10^{-3} + 0.375 \times 10^{-3} = 0.125 \times 10^{-3}$
$\displaystyle I_5=0.125 \ \text{mA} = \frac{1}{8} \ \text{mA}$

Utilizando la ley de Ohm	Utilizando la división de voltaje
$V_c = (3 \ \text{k}) I_5$	$\displaystyle V_c = \left(\frac{3 \ \text{k}}{3 \ \text{k} + 9 \ \text{k}} \right) V_b$
$V_c = (3 \ \text{k})(0.125 \ \text{m})$	$\displaystyle V_c = \left(\frac{3 \ \text{k}}{3 \ \text{k} + 9\ \text{k}} \right)(1.5 \ \text{m})$
$V_c = (3 \times 10^3)(0.125 \times 10^{-3}) = 0.375 \times 10^{-3}$	$\displaystyle V_c = \left(\frac{3 \times 10^{3}}{3 \times 10^{3} + 9\times 10^{3}} \right)(1.5 \times 10^{-3}) = 0.375 \ \times 10^{-3}$
$\displaystyle V_c = 0.375 \ \text{V} = \frac{3}{8} \ \text{V}$	$\displaystyle \therefore V_c = 0.375 \ \text{V} = \frac{3}{8} \ \text{V}$

Circuitos con combinaciones de resistores en serie y en paralelo. Circuitos eléctricos.

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Circuitos con combinaciones de resistores en serie y en paralelo. Circuitos eléctricos.

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta