Equilibrio de rotación. Física.

Introducción

Un cuerpo está en equilibrio de rotación si no tiene ningún momento de torsión actuando sobre él. En tales casos, la suma de todos los momentos de torsión respecto de cualquier eje debe ser igual a cero. El eje puede escogerse en cualquier parte porque el sistema no tiende a girar respecto de ningún punto. A esto se le llama segunda condición de equilibrio y puede enunciarse así:

La suma algebraica de todos los momentos de torsión respecto de cualquier punto es cero.

$\sum{M} = M_1 + M_2 + M_3 + \cdots =0$

$\sum{M} =0$

Problemas resueltos

Problema 1. Dos cazadores llevan una pieza cuyo peso es de 500 N, utilizan un tronco de 3 m que pesa 100 N. Si el cuerpo está colgado a una distancia de 1.20 m del primer cazador, calcular la fuerza ejercida por cada persona.

Figura 1.Dos cazadores llevando su presa.

Solución. A continuación se muestra el diagrama de cuerpo libre.

$\overrightarrow{F}_1$ , $\overrightarrow{F}_2$ , $\overrightarrow{F}_3$ y $\overrightarrow{P}$ , actúan sobre el tronco manteniéndolo en equilibrio.

La distancia $AC = 3 \ m$ , la distancia $AB=1.20 \ m$ , $F_3 = 100 \ N$ , y $\overrightarrow{P} = 500 \ N$ .

Aplicando las condiciones de equilibrio se tiene que

$\sum{F} = \overrightarrow{F}_1 + \overrightarrow{F}_2- \overrightarrow{F}_3 - \overrightarrow{P}$

$\overrightarrow{F}_1 + \overrightarrow{F}_2 - \overrightarrow{F}_3 - \overrightarrow{P} = 0$

Entonces

$\overrightarrow{F}_1 + \overrightarrow{F}_2 - 500 \ N - 100 \ N = 0$

$\overrightarrow{F}_1 + \overrightarrow{F}_2 - 600 \ N = 0$

$\overrightarrow{F}_1 + \overrightarrow{F}_2 = 600 \ N$

Con la suma de momentos respecto del punto A se tiene

$(-\overrightarrow{F}_3)(1.50 \ m) - (\overrightarrow{P})(AB) + (\overrightarrow{F}_2)(AC) = 0$

$(-100 \ N)(1.50 \ m) - (500 \ N)(1.20 \ m) + (\overrightarrow{F}_2)(3 \ m) = 0$

$-150 \ Nm - 600 \ Nm + (\overrightarrow{F}_2)(3 \ m) = 0$

$-750 \ Nm + (\overrightarrow{F}_2)(3 \ m) = 0$

Despejando $\overrightarrow{F}_2$ de la ecuación anterior

$(\overrightarrow{F}_2)(3 \ m) = 750 \ Nm$

$\overrightarrow{F}_2 = \frac{750 \ Nm}{3 \ m}$

$\therefore \overrightarrow{F}_2 = 250 \ N$

el valor de $\overrightarrow{F}_1$ se obtiene restando de $\overrightarrow{F}_3 + \overrightarrow{P} = 600 \ N$ .

$\overrightarrow{F}_1 + \overrightarrow{F}_2 = 600 \ N$

$\overrightarrow{F}_1 + 250 \ N = 600 \ N$

$\overrightarrow{F}_1 = 600 \ N - 250 \ N$

$\therefore \overrightarrow{F}_1 = 350 \ N$

Problema 2. Una viga de 10 m de longitud está sostenida por dos pivotes A y B, con un peso de 850 N; soporta una carga de 1000 N que forma un ángulo de 60° y otra de 500 N, como se muestra en la figura 3. Calcular la reacción en los apoyos A y B.

Solución. Los datos son los siguientes

$\overrightarrow{P} = 850 \ N$
$\overrightarrow{F}_1=1000 \ N$
$\theta = 60$ °
$\overrightarrow{F}_2 = 500 \ N$
$A=?$
$B=?$

El esquema es el siguiente

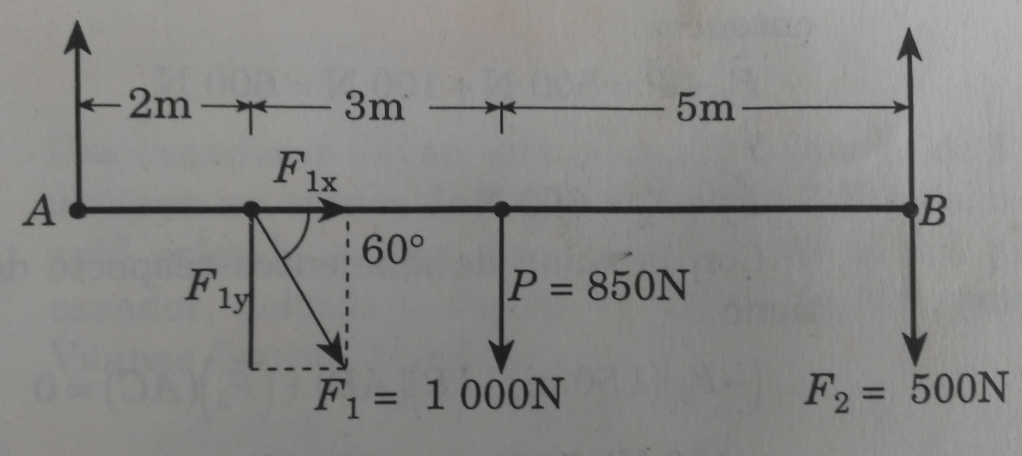
En la figura 3 se observa que la fuerza $F_1$ forma un ángulo de 60° respecto de la horizontal; se debe calcular el valor de su componente vertical, pues es la única que es capaz de hacer girar al cuerpo debido a que su componente horizontal tiene su línea de acción sobre el plano de la viga; por lo tanto, su momento es igual a cero. Por otra parte, el peso de la viga se considera que está a la mitad de su longitud.