Introducción
Se considera el circuito de la siguiente figura. Se observa que esta red tiene el mismo número de elementos contenidos. Sin embargo, al intentar reducir el circuito a una red equivalente con una fuente y un resistor
, en ningún lugar se encuentra un resistor conectado en serie o en paralelo con el otro. Una manera de se poder resolverlo es sustituir una parte de la red por un circuito equivalente, permitiendo reducir con facilidad la combinación de resistores a una sola resistencia equivalente. Esta conversión se denomina transformación Y a delta, o delta a Y.

Se considera las redes de las figuras 2 y 3, respectivamente. Se observa que los resistores de la figura 2 forman una Δ (delta), mientras que en la figura 3 forman una Y. Si ambas configuraciones se conectan únicamente en las tres terminales ,
y
, sería de gran utilidad establecer una equivalencia entre ellas; es posible relacionar las resistencias de una red con las de la otra, de tal forma que las características en sus terminales sean la mismas. La relación entre estas dos configuraciones de red se llama la transformación Y-Δ.
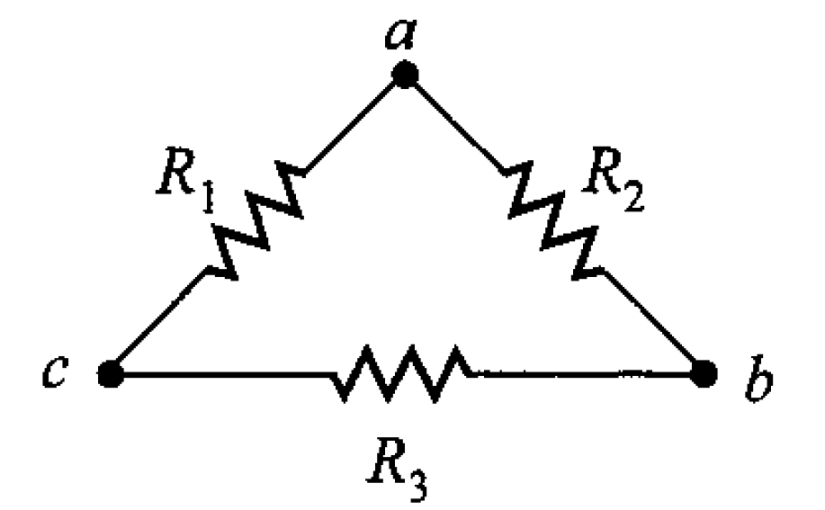
Figura 2. Rede de resistencias en delta. 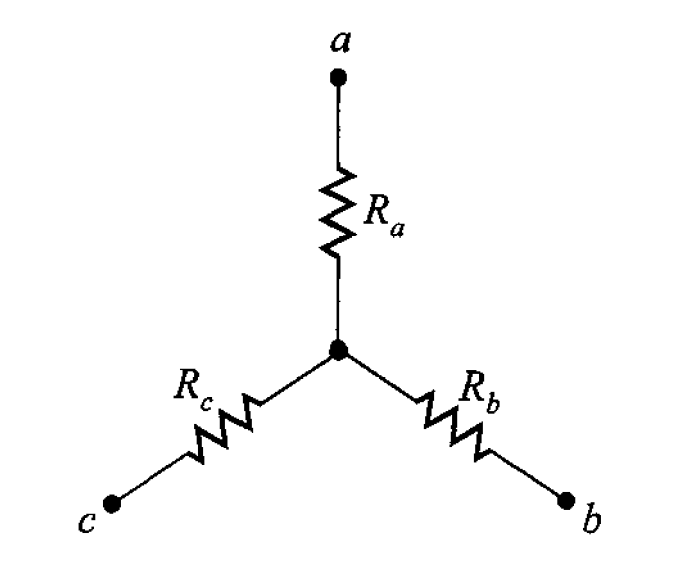
Figura 3. Red de resistencias en Y.
La transformación que relaciona las resistencias ,
y
con
,
y
se deriva como sigue: para que las dos redes sean equivalentes en cada par de terminales correspondientes, es necesario que la resistencia en tales terminales sea la misma (por ejemplo, la resistencia en las terminales
y
con
en circuito abierto, debe ser la misma en ambas redes). Por lo tanto, al igualar las resistencias de cada par de terminales correspondientes, se obtiene las ecuaciones siguientes:
Este conjunto de ecuaciones puede resolverse para ,
y
(esto es una transformación de Δ a Y); sus resultado son
Y también puede resolverse para ,
y
(esto es una transformación de Y a Δ); sus resultados son
Este conjunto de soluciones son relaciones generales, y se aplican a cualquier conunto de resistencias conectadas en Y o en Δ. Para el caso balanceado en el que y
, las ecuaciones anteriores se reducen a
Y
Problema resuelto
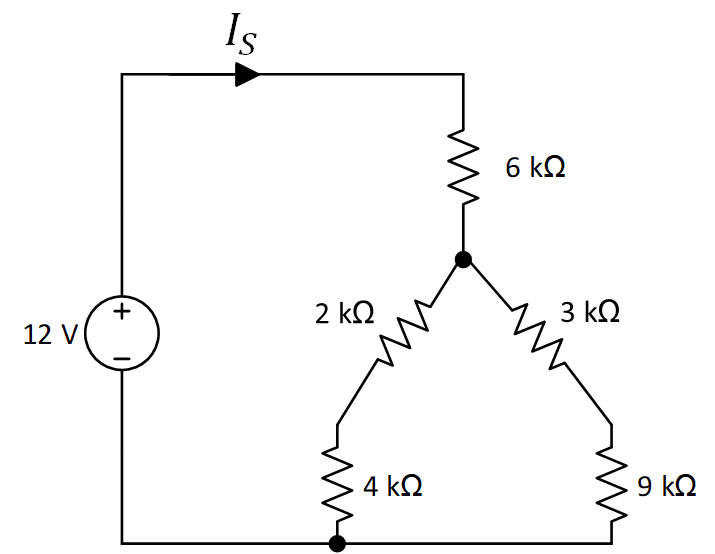
Problema 1. Dada la red de la figura 4, encontrar la corriente de la fuente .
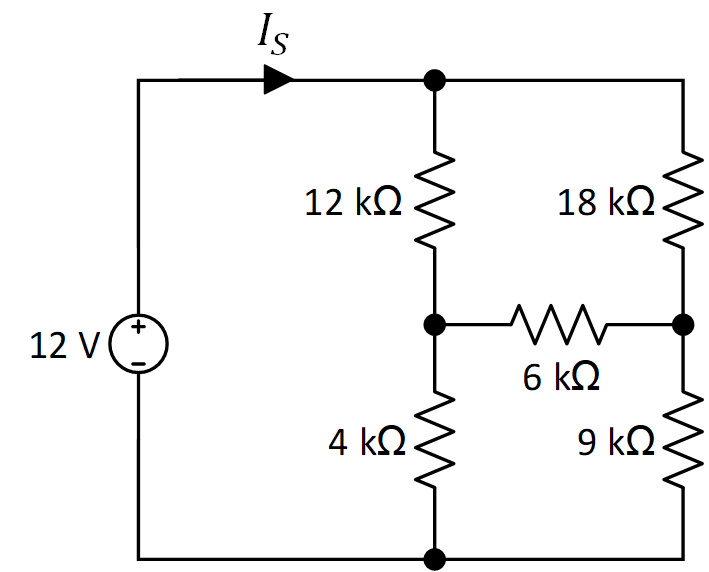
Solución. Se observa que ninguno de los resistores del circuito está en serie o en paralelo. Analizando más a detalle, la red indica que los resistores de 12 kΩ, 6 kΩ y 18 kΩ forman una delta que puede convertirse en una Y

al igual que las resistencias de 4 kΩ, 6 kΩ y 9 kΩ.
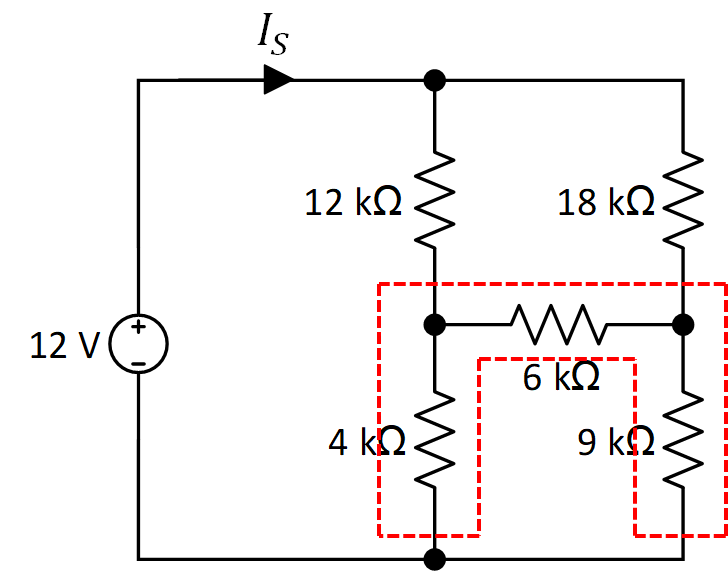
Además, los resistores de 12 kΩ, 6 kΩ y 4 kΩ forman una Y que pude transformarse en una delta
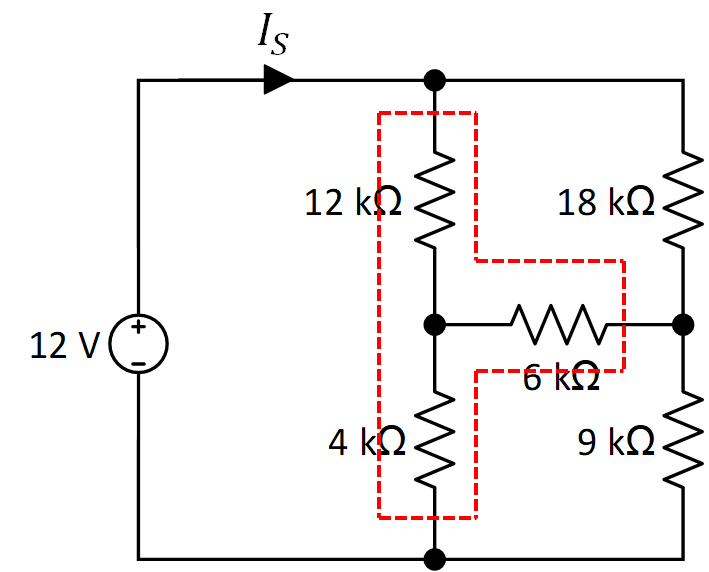
al igual que las resistencias de 18 kΩ, 6 kΩ y 9kΩ.
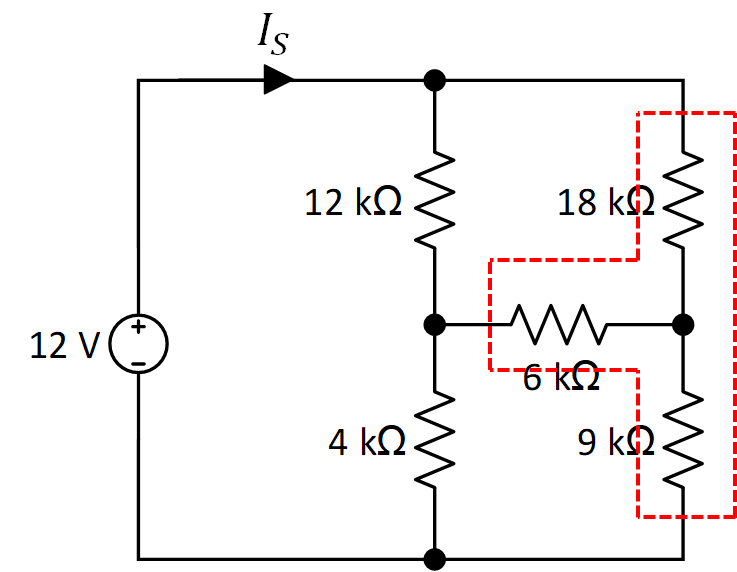
Cualquiera de estas conversiones lleva a una solución. Aquí se aplicará la transformación Δ a Y de los resistores de 12 kΩ, 6 kΩ y 18 kΩ que serán ,
y
(figura 5), que lleva a lo siguiente: el valor de
es
para , su valor es
y el valor de es
Con estos valores, el circuito toma la siguiente forma (figura 9).
Ahora, los resistores de 2 kΩ y 4 kΩ están serie, al igual que los resistores de 3 kΩ y 9kΩ.
El circuito reducido se muestra en la figura 10; se pude observar que las resistencias de 6 kΩ y 12 kΩ están en paralelo (su equivalente es observa en la figura 11).

Figura 10. 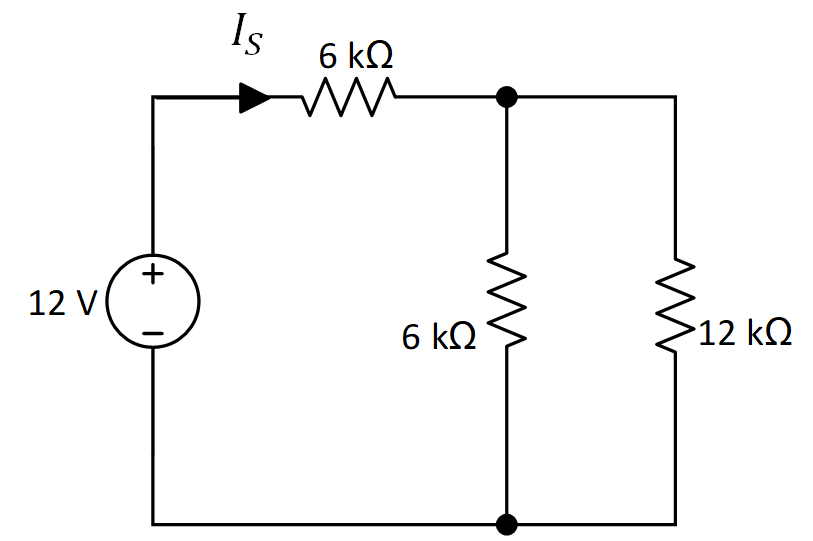
Figura 11.
Calculando las resistencias de 6 kΩ y 12 kΩ que están en paralelo, resulta
La última reducción del circuito de la figura 11 se ilustra en la figura 12.

Con esta última reducción, ya es posible calcular con solo utilizar la ley de Ohm. Entonces,
Despejando