Análisis de nodos para circuitos con fuentes de corriente dependientes. Circuitos eléctricos.

Introducción

Se considera el circuito con una fuente de corriente controlada por corriente mostrado en la figura 1.

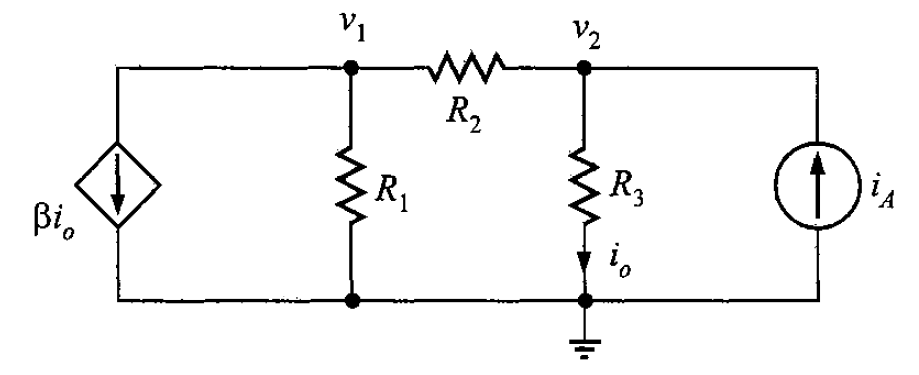
Figura 1. Circuito con una fuente de corriente dependiente.

En el nodo 1, aplicando la LKC, su ecuación es

$\displaystyle \sum_{j=1}^{n}{i_j} = 0$

$\displaystyle \beta i_o + \frac{v_1}{R_1} + \frac{v_1 - v_2}{R_2} = 0$

Como $\displaystyle i_o = \frac{v_2}{R_3}$ , resulta que

$\displaystyle \beta \left(\frac{v_2}{R_3} \right) + \frac{v_1}{R_1} + \frac{v_1 - v_2}{R_2} = 0$

$\displaystyle \left(\frac{\beta}{R_3} \right) v_2 + \frac{v_1}{R_1} + \frac{v_1}{R_2} - \frac{v_2}{R_2} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 + \left(\frac{\beta}{R_3} - \frac{1}{R_2} \right) v_2 = 0$

Figura 2. Señalando el nodo 1 para el análisis de LKC.

En el nodo 2, aplicando la LKC, su ecuación es

$\displaystyle \sum_{j=1}^{n}{i_j} = 0$

$\displaystyle \frac{v_2- v_1}{R_2} + \frac{v_2}{R_3} - i_A = 0$

$\displaystyle \frac{v_2}{R_2} - \frac{v_1}{R_2} + \frac{v_2}{R_3} - i_A = 0$

$\displaystyle - \left(\frac{1}{R_2} \right) v_1 + \left(\frac{1}{R_2} + \frac{1}{R_3} \right) v_2 = i_A$

*Figura 3. Señalando el nodo 2 para el análisis de LKC.*

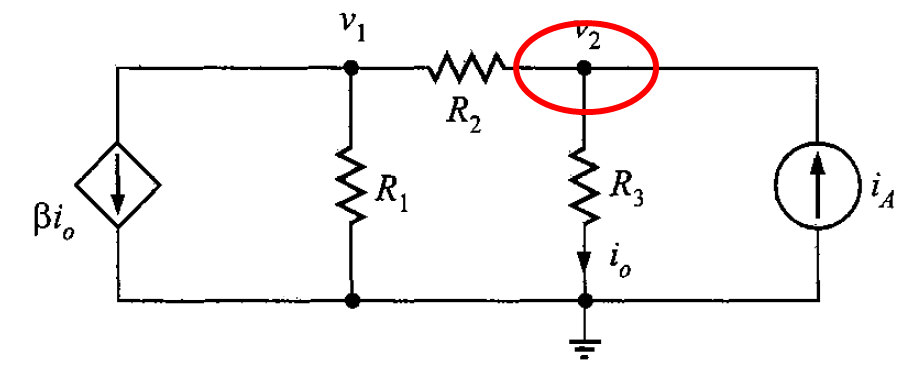
Así que el sistema de ecuaciones es

\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 + \left(\frac{\beta}{R_3} - \frac{1}{R_2} \right) v_2 = 0

\displaystyle - \left(\frac{1}{R_2} \right) v_1 + \left(\frac{1}{R_2} + \frac{1}{R_3} \right) v_2 = i_A

Recordando que $\displaystyle G = \frac{1}{R}$

\displaystyle \left(G_1 + G_2 \right) v_1 + \left(\beta G_3 - G_2 \right) v_2 = 0

\displaystyle - G_2 v_1 + \left(G_2 + G_3 \right) v_2 = i_A

Problemas resueltos

Problema 1. Determine los voltajes de nodo y las corrientes de rama en la red de la figura 4 con base en los siguientes parámetros: $\beta = 2$ , $R_1 = 12 \ \text{k} \Omega$ , $R_2 = 6 \ \text{k} \Omega$ , $R_3 = 3 \ \text{k} \Omega$ , $i_A = 2 \ \text{mA}$ .

Solución.

En el nodo 1, aplicando la LKC, su ecuación es

$\displaystyle \sum_{j=1}^{n}{i_j} = 0$

$\displaystyle \beta i_o + \frac{v_1}{R_1} + \frac{v_1 - v_2}{R_2} = 0$

Como $\displaystyle i_o = \frac{v_2}{R_3}$ , resulta que

$\displaystyle \beta \left(\frac{v_2}{R_3} \right) + \frac{v_1}{R_1} + \frac{v_1 - v_2}{R_2} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 + \left(\frac{\beta}{R_3} - \frac{1}{R_2} \right) v_2 = 0$

Figura 5. Señalando el nodo 1 para el análisis de LKC.

En el nodo 2, aplicando la LKC, su ecuación es

$\displaystyle \sum_{j=1}^{n}{i_j} = 0$

$\displaystyle \frac{v_2- v_1}{R_2} + \frac{v_2}{R_3} - i_A = 0$

$\displaystyle \frac{v_2}{R_2} - \frac{v_1}{R_2} + \frac{v_2}{R_3} - i_A = 0$

$\displaystyle - \left(\frac{1}{R_2} \right) v_1 + \left(\frac{1}{R_2} + \frac{1}{R_3} \right) v_2 = i_A$

*Figura 6. Señalando el nodo 2 para el análisis de LKC.*

Así que el sistema de ecuaciones es

Recordando los parámetros: $\beta = 2$ , $R_1 = 12 \ \text{k} \Omega$ , $R_2 = 6 \ \text{k} \Omega$ , $R_3 = 3 \ \text{k} \Omega$ , $i_A = 2 \ \text{mA}$ , se sustituyen en el sistema de ecuaciones.

\displaystyle \left(\frac{1}{12 \ \text{k}} + \frac{1}{6 \ \text{k}} \right) v_1 + \left(\frac{2}{3 \ \text{k}} - \frac{1}{6 \ \text{k}} \right) v_2 = 0

\displaystyle - \left(\frac{1}{6 \ \text{k}} \right) v_1 + \left(\frac{1}{6 \ \text{k}} + \frac{1}{3 \ \text{k}} \right) v_2 = 2 \ \text{m}

Simplificando

\displaystyle \left(\frac{1}{4 \ \text{k}} \right) v_1 + \left(\frac{1}{2 \ \text{k}} \right) v_2 = 0

\displaystyle - \left(\frac{1}{6 \ \text{k}} \right) v_1 + \left(\frac{1}{2 \ \text{k}} \right) v_2 = 2 \ \text{m}

Expresándolo en forma matricial

$\displaystyle \left[\begin{matrix} \frac{1}{4 \ \text{k}} & \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{6 \ \text{k}} & \frac{1}{2 \ \text{k}} \end{matrix} \right] \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \left[\begin{matrix} 0 \\ 2 \ \text{m} \end{matrix} \right]$

Su forma general es

$\bold{G} \bold{V} = \bold{I}$

Para llegar al resultado

$\bold{V} = \bold{G}^{-1} \bold{I}$

es necesario obtener la inversa de $\bold{G}$ , y para ello se debe determinar su matriz adjunta traspuesta y su determinante. La determinante de $\bold{G}$ es

$\displaystyle \text{det} \ \bold{G} = \left[\begin{matrix} \frac{1}{4 \ \text{k}} & \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{6 \ \text{k}} & \frac{1}{2 \ \text{k}} \end{matrix} \right]$

$\displaystyle \text{det} \ \bold{G} = \left(\frac{1}{4 \ \text{k}} \right) \left(\frac{1}{2 \ \text{k}} \right) - \left(- \frac{1}{6 \ \text{k}} \right) \left(\frac{1}{2 \ \text{k}} \right)$

$\displaystyle \text{det} \ \bold{G} = \left(\frac{1}{8 \ \text{k}^2} \right) - \left(- \frac{1}{12 \ \text{k}^2} \right) = \frac{1}{8 \ \text{k}^2} + \frac{1}{12 \ \text{k}^2}$

$\displaystyle \text{det} \ \bold{G} = \frac{5}{24 \ \text{k}^2}$

La matriz adjunta de $\bold{G}$ , se debe determinar los menores de la misma

$\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right]$

\displaystyle C_{11} = {(-1)}^{1+1} \left(\frac{1}{2 \ \text{k}} \right) = \frac{1}{2 \ \text{k}}

\displaystyle C_{12} = {(-1)}^{1+2} \left(- \frac{1}{6 \ \text{k}} \right) = \frac{1}{6 \ \text{k}}

así que

$\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right]$

$\displaystyle Adj \ \bold{G} = \left[\begin{matrix} \frac{1}{2 \ \text{k}} & \frac{1}{6 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & \frac{1}{4 \ \text{k}} \end{matrix} \right]$

y la traspuesta de la matriz adjunta de $\bold{G}$ es

$\displaystyle {\left(Adj \ \bold{G}\right)}^T = \left[\begin{matrix} \frac{1}{2 \ \text{k}} & - \frac{1}{2 \ \text{k}} \\ \\ \frac{1}{6 \ \text{k}} & \frac{1}{4 \ \text{k}} \end{matrix} \right]$

Entonces, la inversa de $\bold{G}^{-1}$ es

$\displaystyle \bold{G}^{-1} = \frac{{\left(Adj \ \bold{G}\right)}^T}{\text{det} \ \bold{G}} = \left(\frac{1}{\text{det} \ \bold{G}} \right) {\left(Adj \ \bold{G}\right)}^T$

$\displaystyle \bold{G}^{-1} = \left(\frac{1}{\frac{5}{24 \ \text{k}^2}} \right) \left[\begin{matrix} \frac{1}{2 \ \text{k}} & - \frac{1}{2 \ \text{k}} \\ \\ \frac{1}{6 \ \text{k}} & \frac{1}{4 \ \text{k}} \end{matrix} \right]$

$\displaystyle \bold{G}^{-1} = \left(\frac{24 \ \text{k}^2}{5} \right) \left[\begin{matrix} \frac{1}{2 \ \text{k}} & - \frac{1}{2 \ \text{k}} \\ \\ \frac{1}{6 \ \text{k}} & \frac{1}{4 \ \text{k}} \end{matrix} \right] = \left[\begin{matrix} \frac{1}{2 \ \text{k}} \left(\frac{24 \ \text{k}^2}{5} \right) & - \frac{1}{2 \ \text{k}} \left(\frac{24 \ \text{k}^2}{5} \right) \\ \\ \frac{1}{6 \ \text{k}} \left(\frac{24 \ \text{k}^2}{5} \right) & \frac{1}{4 \ \text{k}} \left(\frac{24 \ \text{k}^2}{5} \right) \end{matrix} \right]$

$\displaystyle \bold{G}^{-1} = \left[\begin{matrix} \frac{12}{5} \ \text{k} & - \frac{12}{5} \ \text{k} \\ \\ \frac{4}{5} \ \text{k} & \frac{6}{5} \ \text{k} \end{matrix} \right]$

Regresando a la expresión matricial

$\displaystyle \bold{G} \bold{V} = \bold{I}$

$\displaystyle \left[\begin{matrix} \frac{1}{4 \ \text{k}} & \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{6 \ \text{k}} & \frac{1}{2 \ \text{k}} \end{matrix} \right] \left[\begin{matrix} v_1 \\ v_2 \end{matrix} \right] = \left[\begin{matrix} 0 \\ 2 \ \text{m} \end{matrix} \right]$

Despejando $\bold{V}$ ,

$\displaystyle \bold{V} = \bold{G}^{-1} \bold{I}$

$\displaystyle \left[\begin{matrix} v_1 \\ v_2 \end{matrix} \right] = \left[\begin{matrix} \frac{12}{5} \ \text{k} & - \frac{12}{5} \ \text{k} \\ \\ \frac{4}{5} \ \text{k} & \frac{6}{5} \ \text{k} \end{matrix} \right] \left[\begin{matrix} 0 \\ 2 \ \text{m} \end{matrix} \right]$

Realizando la multiplicación matricial en el segundo miembro (sin olvidar que $\text{k} = 1 \times 10^3$ y $\text{m} = 1 \times 10^{-3}$ ), resulta

$\displaystyle \left[\begin{matrix} v_1 \\ v_2 \end{matrix} \right] = \left[\begin{matrix} \frac{12}{5} \times 10^3 & - \frac{12}{5} \times 10^3 \\ \\ \frac{4}{5} \times 10^3 & \frac{6}{5} \times 10^3 \end{matrix} \right] \left[\begin{matrix} 0 \\ 2 \times 10^{-3} \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} v_1 \\ v_2 \end{matrix} \right] = \left[\begin{matrix} \left(\frac{12}{5} \times 10^3 \right) \left(0 \right) + \left(- \frac{12}{5} \times 10^3 \right) \left(2 \times 10^{-3} \right) \\ \\ \left(\frac{4}{5} \times 10^3 \right) (0) + \left(\frac{6}{5} \times 10^3 \right) \left(2 \times 10^{-3} \right) \end{matrix} \right] = \left[\begin{matrix} 0 - \frac{24}{5} \\ \\ 0 + \frac{12}{5} \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} v_1 \\ v_2 \end{matrix} \right] = \left[\begin{matrix} - \frac{24}{5} \\ \\ \frac{12}{5} \end{matrix} \right]$

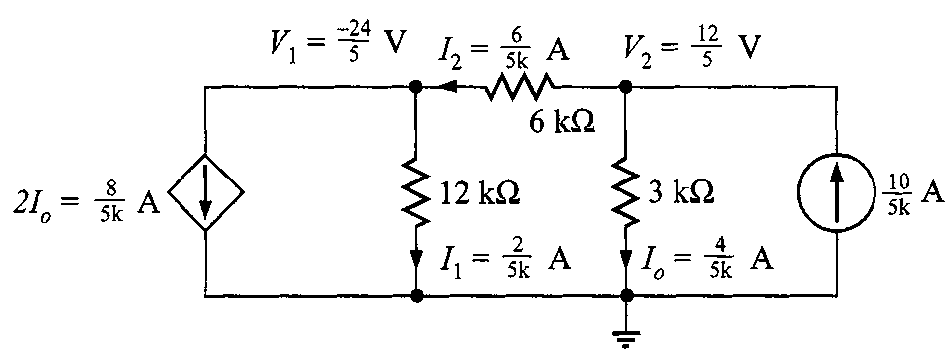
Así que los voltajes en cada nodo son $\displaystyle v_1 = - \frac{24}{5}$ y $\displaystyle v_2 = \frac{12}{5}$ . Ahora solo falta calcular las corrientes de rama.

La corriente que pasa a través de $R_3$ es

$\displaystyle i_o = \frac{v_2}{R_3}$

$\displaystyle i_o = \frac{\frac{12}{5}}{3 \ \text{k}} = \frac{\frac{12}{5}}{3 \times 10^{3}} = \frac{12}{15 \times 10^{3}} = \frac{4}{5} \times 10^{-3}$

$\displaystyle i_o = \frac{4}{5} \ \text{mA}$

La corriente que pasa a través de $R_2$ es

$\displaystyle I_2 = \frac{v_2-v_1}{R_2}$

$\displaystyle I_2 = \frac{\frac{12}{5} - \left(- \frac{24}{5} \right)}{6 \ \text{k}} = \frac{\frac{12}{5} + \frac{24}{5}}{6 \ \text{k}} = \frac{\frac{36}{5}}{6 \ \text{k}}$

$\displaystyle I_2 = \frac{\frac{36}{5}}{6 \times 10^{3}} = \frac{36}{30} \times 10^{-3} = \frac{6}{5} \times 10^{-3}$

$\displaystyle I_2 = \frac{6}{5} \ \text{mA}$

La figura 7 muestra todos los resultados obtenidos.

Figura 7. Circuito que ilustra todos los resultados calculados durante el problema 1.

Problema 2. Determinar el conjunto de ecuaciones linealmente independientes cuya solución produce los voltajes de nodo para la red de la figura 8. Calcule después los voltajes de nodo dados los siguientes valores para los componentes: $R_1 = 1 \ \text{k} \Omega$ , $R_2 = R_3 = 2 \ \text{k} \Omega$ , $R_4 = 4 \ \text{k} \Omega$ , $i_A = 2 \ \text{mA}$ , $i_B = 4 \ \text{mA}$ y $\alpha = 2$ .

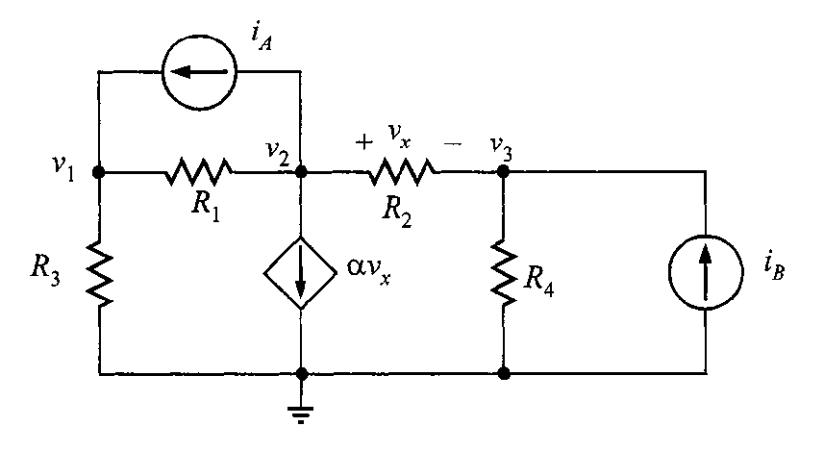
Solución. Se analiza cada nodo utilizando la LKC. En el nodo 1 se tiene

Figura 9. Análisis del nodo 1 utilizando LKC.

$\displaystyle \sum_{j=1}^{n}{i_j} = 0$

$\displaystyle \frac{v_1}{R_3} + \frac{v_1 - v_2}{R_1} - i_A = 0$

$\displaystyle \frac{v_1}{R_3} + \frac{v_1}{R_1} - \frac{v_2}{R_1} - i_A = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_3} \right) v_1 - \left(\frac{1}{R_1} \right) v_2 = i_A$

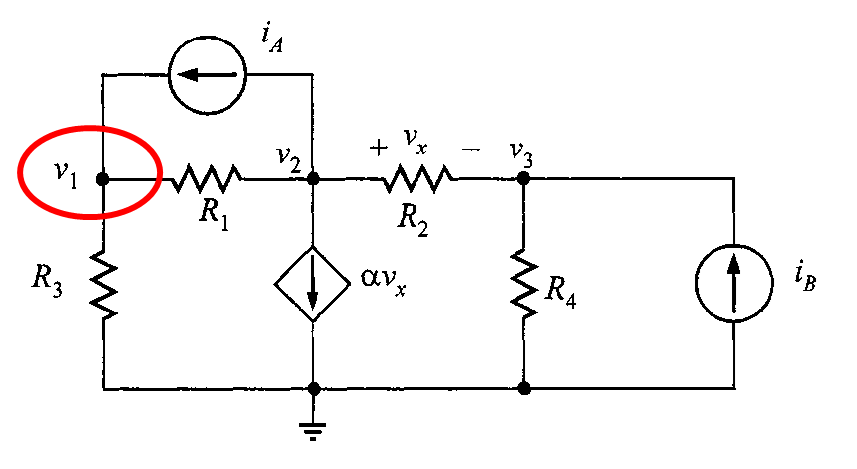
En el nodo 2, se tiene

*Figura 10. Análisis del nodo 2 utilizando LKC.*

$\displaystyle \sum_{j=1}^{n}{i_j} = 0$

$\displaystyle \alpha v_x + \frac{v_2 - v_3}{R_2} + \frac{v_2 - v_1}{R_1} + i_A = 0$

Si $v_x = v_2 - v_3$ , entonces

$\displaystyle \alpha (v_2 - v_3) + \frac{v_2 - v_3}{R_2} + \frac{v_2 - v_1}{R_1} + i_A = 0$

$\displaystyle \alpha v_2 - \alpha v_3 + \frac{v_2}{R_2} - \frac{v_3}{R_2} + \frac{v_2}{R_1} - \frac{v_1}{R_1} + i_A = 0$

$\displaystyle - \left(\frac{1}{R_1} \right) v_1 + \left(\alpha + \frac{1}{R_1} + \frac{1}{R_2} \right) v_2 - \left(\alpha + \frac{1}{R_2} \right) v_3 = - i_A$

Y en el nodo 3,

*Figura 10. Análisis del nodo 3 utilizando LKC.*

$\displaystyle \sum_{j=1}^{n}{i_j} = 0$

$\displaystyle \frac{v_3 - v_2}{R_2} + \frac{v_3}{R_4} - i_B = 0$

$\displaystyle \frac{v_3}{R_2} - \frac{v_2}{R_2} + \frac{v_3}{R_4} - i_B = 0$

$\displaystyle - \left(\frac{1}{R_2} \right) v_2 + \left(\frac{1}{R_2} + \frac{1}{R_4} \right) v_3 = i_B$

Tomando todas las ecuaciones calculadas en cada nodo, se tiene el siguiente sistemas de ecuaciones

\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_3} \right) v_1 - \left(\frac{1}{R_1} \right) v_2 = i_A

\displaystyle - \left(\frac{1}{R_1} \right) v_1 + \left(\alpha + \frac{1}{R_1} + \frac{1}{R_2} \right) v_2 - \left(\alpha + \frac{1}{R_2} \right) v_3 = - i_A

Recordando los parámetros del problema $R_1 = 1 \ \text{k} \Omega$ , $R_2 = R_3 = 2 \ \text{k} \Omega$ , $R_4 = 4 \ \text{k} \Omega$ , $i_A = 2 \ \text{mA}$ , $i_B = 4 \ \text{mA}$ y $\alpha = 2$ , al sustituirlos resulta

\displaystyle \left(\frac{1}{1 \ \text{k}} + \frac{1}{2 \ \text{k}} \right) v_1 - \left(\frac{1}{1 \ \text{k}} \right) v_2 = 2 \ \text{m}

\displaystyle - \left(\frac{1}{1 \ \text{k}} \right) v_1 + \left(2 + \frac{1}{1 \ \text{k}} + \frac{1}{2 \ \text{k}} \right) v_2 - \left(2 + \frac{1}{2 \ \text{k}} \right) v_3 = - 2 \ \text{m}

Simplificando

\displaystyle \left(\frac{3}{2 \ \text{k}} \right) v_1 - \left(\frac{1}{1 \ \text{k}} \right) v_2 = 2 \ \text{m}

\displaystyle - \left(\frac{1}{1 \ \text{k}} \right) v_1 + \left(\frac{4 \ \text{k} + 3}{2 \ \text{k}} \right) v_2 - \left(\frac{4 \ \text{k} + 1}{2 \ \text{k}} \right) v_3 = - 2 \ \text{m}

Por esta ocasión cada coeficiente se expresará en términos decimales. Así que

\displaystyle 0.0015 v_1 - 0.001 v_2 = 0.002

\displaystyle - 0.001 v_1 + 2.0015 v_2 - 2.0005 v_3 = - 0.002

Expresando este sistema de ecuaciones en forma matricial resulta

$\displaystyle \left[\begin{matrix} 0.0015 & -0.001 & 0 \\ -0.001 & 2.0015 & -2.0005 \\ 0 & -0.0005 & 0.00075 \end{matrix} \right] \left[\begin{matrix} v_1 \\ v_2 \\ v_3\end{matrix} \right] = \left[\begin{matrix} 0.002 \\ -0.002 \\ 0.004 \end{matrix} \right]$

Que es similar a

$\displaystyle \bold{G} \bold{V} = \bold{I}$

Despejando $\bold{V}$

$\displaystyle \bold{V} = \bold{G}^{-1} \bold{I}$

Así que es necesario determinar la inversa de $\bold{G}$ , donde

$\displaystyle \bold{G} = \left[\begin{matrix} 0.0015 & -0.001 & 0 \\ -0.001 & 2.0015 & -2.0005 \\ 0 & -0.0005 & 0.00075 \end{matrix} \right]$

El determinante de $\bold{G}$ es

$\displaystyle \text{det} \ \bold{G} = \left|\begin{matrix} 0.0015 & -0.001 & 0 \\ -0.001 & 2.0015 & -2.0005 \\ 0 & -0.0005 & 0.00075 \end{matrix} \right|$

$\displaystyle \text{det} \ \bold{G} = 0.00000075056$

La matriz adjunta de $\bold{G}$ es

$\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right]$

donde $C_{ij}$ es el cofactor correspondiente y se calcula utilizando la fórmula

$\displaystyle C_{ij} = {(-1)}^{i+j} \ M_{ij}$

donde $M_{ij}$ es el menor del elemento $g_{ij}$ y para encontrar el valor de cada menor, se realiza lo siguiente

$\displaystyle M_{11} = \left|\begin{matrix} 2.0015 & -2.0005 \\ -0.0005 & 0.00075 \end{matrix} \right| = 0.000500875$

$\displaystyle M_{12} = \left|\begin{matrix} -0.001 & -2.0005 \\ 0 & 0.00075 \end{matrix} \right| = -0.00000075$

$\displaystyle M_{13} = \left|\begin{matrix} -0.001 & 2.0015 \\ 0 & -0.0005 \end{matrix} \right|=0.0000005$

$\displaystyle M_{21} = \left|\begin{matrix} -0.001 & 0 \\ -0.0005 & 0.00075 \end{matrix} \right| = - 0.00000075$

$\displaystyle M_{22} = \left|\begin{matrix} 0.0015 & 0 \\ 0 & 0.00075 \end{matrix} \right| = 0.000001125$

$\displaystyle M_{23} = \left|\begin{matrix} 0.0015 & -0.001 \\ 0 & -0.0005 \end{matrix} \right| = -0.00000075$

$\displaystyle M_{31} = \left|\begin{matrix} -0.001 & 0 \\ 2.0015 & -2.0005 \end{matrix} \right|=0.00200005$

$\displaystyle M_{32} = \left|\begin{matrix} 0.0015 & 0 \\ -0.001 & -2.0005 \end{matrix} \right| = - 0.00300075$

$\displaystyle M_{33} = \left|\begin{matrix} 0.0015 & -0.001 \\ -0.001 & 2.0015 \end{matrix} \right| = 0.00300125$

Teniendo los resultados de cada menor, se puede calcular cada cofactor

\displaystyle C_{11} = M_{11} = 0.000500875

\displaystyle C_{12} = -M_{12} = 0.0000007

Así, la matriz adjunta es

$\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right]$

$\displaystyle Adj \ \bold{G} = \left[\begin{matrix} 0.000500875 & 0.0000007 & 0.0000005 \\ 0.00000075 & 0.000001125 & 0.00000075 \\ 0.00200005 & 0.00300075 & 0.00300125 \end{matrix} \right]$

Por lo que su traspuesta es

$\displaystyle {(Adj \ \bold{G})}^T = \left[\begin{matrix} 0.000500875 & 0.00000075 & 0.00200005 \\ 0.0000007 & 0.000001125 & 0.00300075 \\ 0.0000005 & 0.00000075 & 0.00300125 \end{matrix} \right]$

Así que, la matriz inversa de $\bold{G}$ es

$\displaystyle \bold{G}^{-1} = \frac{{\left(Adj \ \bold{G}\right)}^T}{\text{det} \ \bold{G}} = \left(\frac{1}{\text{det} \ \bold{G}} \right) {\left(Adj \ \bold{G}\right)}^T$

$\displaystyle \bold{G}^{-1} = \left(\frac{1}{0.00000075056} \right) \left[\begin{matrix} 0.000500875 & 0.00000075 & 0.00200005 \\ 0.0000007 & 0.000001125 & 0.00300075 \\ 0.0000005 & 0.00000075 & 0.00300125 \end{matrix} \right]$

$\displaystyle \bold{G}^{-1} = \left(1,332,338.521 \right) \left[\begin{matrix} 0.000500875 & 0.00000075 & 0.00200005 \\ 0.0000007 & 0.000001125 & 0.00300075 \\ 0.0000005 & 0.00000075 & 0.00300125 \end{matrix} \right]$

$\displaystyle \bold{G}^{-1} = \left[\begin{matrix} 667.335 & 0.999 & 2664.744 \\ 0.933 & 1.499 & 3998.015 \\ 0.666 & 0.999 & 3998.681 \end{matrix} \right]$

Regresando a la expresión matricial

$\displaystyle \bold{G} \bold{V} = \bold{I}$

Despejando $\bold{V}$

$\displaystyle \bold{V} = \bold{G}^{-1} \bold{I}$

$\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3\end{matrix} \right] = \left[\begin{matrix} 667.335 & 0.999 & 2664.744 \\ 0.933 & 1.499 & 3998.015 \\ 0.666 & 0.999 & 3998.681 \end{matrix} \right] \left[\begin{matrix} 0.002 \\ -0.002 \\ 0.004 \end{matrix} \right]$

Realizando la multiplicación matricial en el segundo miembro resulta

$\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3\end{matrix} \right] = \left[\begin{matrix} 667.335(0.002) + 0.999(-0.002) + 2664.744(0.004) \\ 0.933(0.002) + 1.499(-0.002) + 3998.015(0.004) \\ 0.666(0.002) + 0.999(-0.002) + 3998.681(0.004) \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3\end{matrix} \right] = \left[\begin{matrix} 1.33467 - 0.0020 + 10.6590 \\ 0.0019 - 0.0030 + 15.9921 \\ 0.0013 - 0.0020 + 15.9948 \end{matrix} \right]$

$\displaystyle \therefore \left[\begin{matrix} v_1 \\ v_2 \\ v_3\end{matrix} \right] = \left[\begin{matrix} 11.99167 \\ 15.991 \\ 15.9941 \end{matrix} \right]$

Finalmente, los voltajes de cada nodo son $v_1 = 11.99167 \ \text{V}$ , $v_2 = 15.991 \ \text{V}$ y $v_3 = 15.9941 \ \text{V}$ .

$\displaystyle C_{11} = {(-1)}^{1+1} \left(\frac{1}{2 \ \text{k}} \right) = \frac{1}{2 \ \text{k}}$	$\displaystyle C_{12} = {(-1)}^{1+2} \left(- \frac{1}{6 \ \text{k}} \right) = \frac{1}{6 \ \text{k}}$
$\displaystyle C_{21} = {(-1)}^{2+1} \left(\frac{1}{2 \ \text{k}} \right) = - \frac{1}{2 \ \text{k}}$	$\displaystyle C_{22} = {(-1)}^{2+2} \left(\frac{1}{4 \ \text{k}} \right) = \frac{1}{4 \ \text{k}}$

$\displaystyle C_{11} = M_{11} = 0.000500875$	$\displaystyle C_{12} = -M_{12} = 0.0000007$	$\displaystyle C_{13} = M_{13} = 0.0000005$
$\displaystyle C_{21} = - M_{21} = 0.00000075$	$\displaystyle C_{22} = M_{22} = 0.000001125$	$\displaystyle C_{23} = - M_{23} = 0.00000075$
$\displaystyle C_{31} = M_{31} = 0.00200005$	$\displaystyle C_{32} = - M_{32} = 0.00300075$	$\displaystyle C_{33} = M_{33} = 0.00300125$

Análisis de nodos para circuitos con fuentes de corriente dependientes. Circuitos eléctricos.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Análisis de nodos para circuitos con fuentes de corriente dependientes. Circuitos eléctricos.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta