Análisis de nodos para circuitos con fuentes de voltaje dependientes. Circuitos eléctricos.

Problemas resueltos

Problema 1. Se desea encontrar $I_o$ en la red de la figura 1.

Solución. Se observa (en la figura 1) que la fuente de voltaje independiente está conectada entre el nodo que no es de referencia nombrado como $V_1$ y el de referencia, una de las dos ecuaciones linealmente independientes es

$\displaystyle V_1 = 3 \ \text{V}$

Y la ecuación de control es

$\displaystyle I_x = \frac{V_2}{6 \ \text{k}}$

Luego, aplicando la LKC en el nodo 2, resulta

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle -2I_x + \frac{V_2}{6 \ \text{k}} + \frac{V_2 - V_1}{3 \ \text{k}} = 0$

Sabiendo que $V_1 = 3$ y $\displaystyle I_x = \frac{V_2}{6 \ \text{k}}$ ,

$\displaystyle -2 \left(\frac{V_2}{6 \ \text{k}} \right) + \frac{V_2}{6 \ \text{k}} + \frac{V_2 - 3}{3 \ \text{k}} = 0$

$\displaystyle - \frac{2 V_2}{6 \ \text{k}} + \frac{V_2}{6 \ \text{k}} + \frac{V_2}{3 \ \text{k}} - \frac{3}{3 \ \text{k}} = 0$

$\displaystyle \left(- \frac{2}{6 \ \text{k}} + \frac{1}{6 \ \text{k}} + \frac{1}{3 \ \text{k}} \right) V_2 - \frac{1}{1 \ \text{k}} = 0$

$\displaystyle V_2 = 6 \ \text{k}$

Figura 2. Indicando el nodo 2 del circuito para el análisis de LKC.

Finalmente, la corriente $I_o$ se obtiene

$\displaystyle I_o = \frac{V_2}{6 \ \text{k}}$

$\displaystyle I_o = \frac{6}{6 \ \text{k}} = \frac{6}{6 \times 10^3} = 1 \times 10^{-3}$

$\displaystyle \therefore I_o = 1 \ \text{mA}$

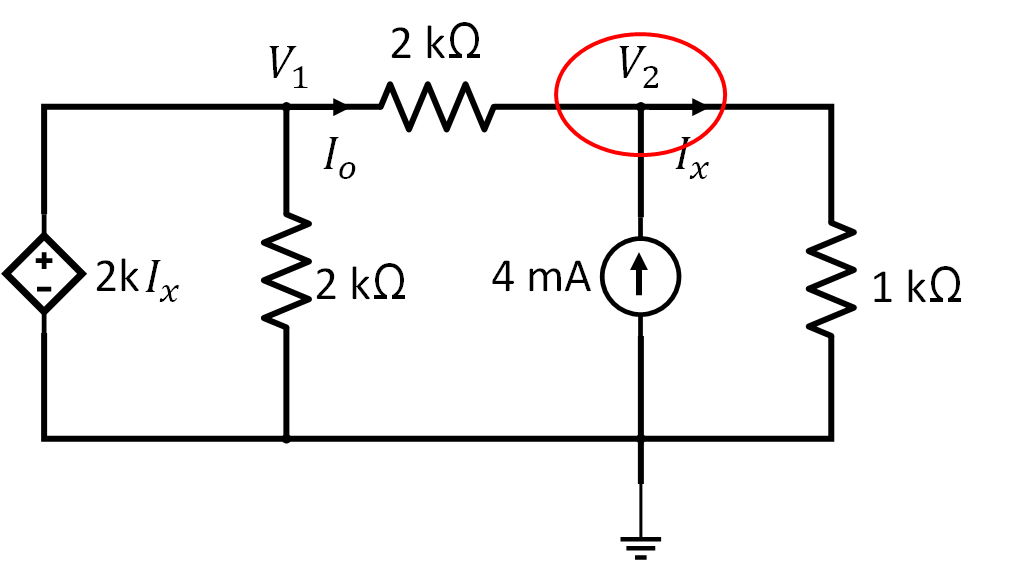
Problema 2. Hallar $I_o$ en la red de la figura 3.

Solución. Se observa (en la figura 3) que de voltaje dependiente está conectada entre el nodo $V_1$ y el nodo de referencia.

$\displaystyle V_1 = (2 \ \text{k}) I_x$

Y también

$\displaystyle I_x = \frac{V_2}{1 \ \text{k}}$

Sustituyendo estas dos obtenidas, se tiene que

$\displaystyle V_1 = (2 \ \text{k}) I_x$

$\displaystyle V_1 = (2 \ \text{k}) \left(\frac{V_2}{1 \ \text{k}} \right)$

$\displaystyle V_1 = 2 V_2$

Luego, aplicando la LKC en el nodo 2, resulta

Figura 4. Señalando el nodo 2 para aplicar la LKC.

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{V_2 - V_1}{2 \ \text{k}} - 4 \ \text{m} + \frac{V_2}{1 \ \text{k}} = 0$

$\displaystyle \frac{V_2}{2 \ \text{k}} - \frac{V_1}{2 \ \text{k}} - 4 \ \text{m} + \frac{V_2}{1 \ \text{k}} = 0$

Recordando que $\displaystyle V_1 = 2 V_2$

$\displaystyle \frac{V_2}{2 \ \text{k}} - \frac{2 V_2}{2 \ \text{k}} - 4 \ \text{m} + \frac{V_2}{1 \ \text{k}} = 0$

$\displaystyle \left(\frac{1}{2 \ \text{k}} - \frac{2}{2 \ \text{k}} + \frac{1}{1 \ \text{k}} \right) V_2 = 4 \ \text{m}$

$\displaystyle \left(\frac{1}{2 \ \text{k}} \right) V_2 = 4 \ \text{m}$

$\displaystyle V_2 = (4 \ \text{m})(2 \ \text{k}) = (4 \times 10^3)(2 \times 10^{-3})$

$\displaystyle V_2 = 8 \ \text{V}$

Entonces

$\displaystyle V_1 = 2 V_2$

$\displaystyle V_1 = 2 (8)$

$\displaystyle V_1 = 16 \ \text{V}$

Finalmente, $I_o$ es

$\displaystyle I_o = \frac{V_1 - V_2}{2 \ \text{k}}$

$\displaystyle I_o = \frac{16 - 8}{2 \ \text{k}} = \frac{8}{2 \ \text{k}} = \frac{8}{2 \ \times 10^3} = 4 \times 10^{-3}$

$\displaystyle \therefore I_o = 4 \ \text{mA}$

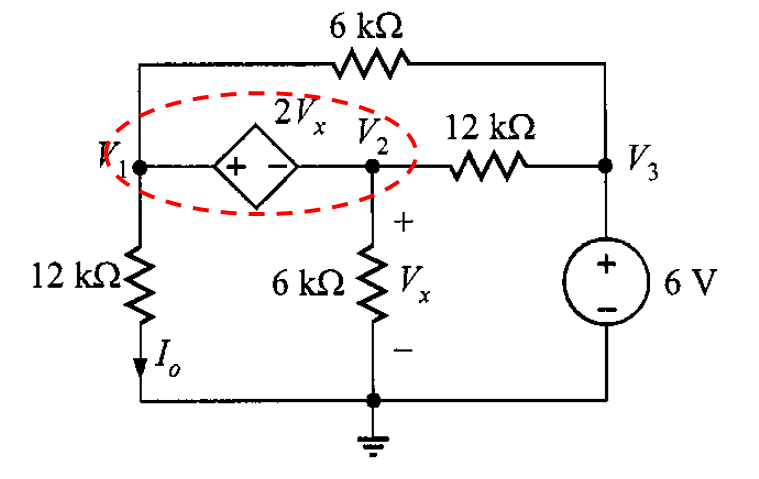
Problema 3. Encontrar la corriente $I_o$ en la red de la figura 5.

Solución. Este circuito contiene tanto una fuente de voltaje independiente como una fuente de voltaje controlada por voltaje. Se observa que $V_3 = 6 \ \text{V}$ , $V_2 = V_x$ , y existe un supernodo entre los nodos $V_1$ y $V_2$ , la cual, su ecuación de restricción es

$\displaystyle V_1 - V_2 = 2 V_x$

Recordando que $V_x = V_2$

$\displaystyle V_1 - V_2 = 2 V_2$

$\displaystyle V_1 = V_2 + 2 V_2$

$\displaystyle V_1 = 3 V_2$

Aplicando la LKC al supernodo se obtiene

Figura 6. Indicando el supernodo del circuito para aplicar LKC.

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{V_1}{12 \ \text{k}} + \frac{V_2}{6 \ \text{k}} + \frac{V_2 - V_3}{12 \ \text{k}} + \frac{V_1 - V_3}{6 \ \text{k}} = 0$

Recordando que $V_1 = 3 V_2$ y $V_3 = 6$ , resulta

$\displaystyle \frac{3 V_2}{12 \ \text{k}} + \frac{V_2}{6 \ \text{k}} + \frac{V_2 - 6}{12 \ \text{k}} + \frac{3V_2 - 6}{6 \ \text{k}} = 0$

$\displaystyle \left(\frac{1}{12 \ \text{k}} + \frac{1}{6 \ \text{k}} + \frac{1}{12 \ \text{k}} + \frac{3}{6 \ \text{k}} \right) V_2 - \frac{6}{12 \ \text{k}} - \frac{6}{6 \ \text{k}} = 0$

$\displaystyle \left(\frac{1}{1 \ \text{k}} \right) V_2 - \frac{18}{12 \ \text{k}} = 0$

$\displaystyle V_2 = \frac{18}{12} = \frac{3}{2} \ \text{V}$

Así que el valor de $V_1$ es

$\displaystyle V_1 = 3 V_2$

$\displaystyle V_1 = 3 \left(\frac{3}{2} \right)$

$\displaystyle V_1 = \frac{9}{2} \ \text{V}$

Finalmente, la corriente $I_o$ es

$\displaystyle I_o = \frac{V_1}{12 \ \text{k}}$

$\displaystyle I_o = \frac{\frac{9}{2}}{12 \ \text{k}} = \frac{\frac{9}{2}}{12 \times 10^3} = \frac{9}{24} \times 10^{-3} = \frac{3}{8} \times 10^{-3}$

$\displaystyle \therefore I_o = \frac{3}{8} \ \text{mA}$

Análisis de nodos para circuitos con fuentes de voltaje dependientes. Circuitos eléctricos.

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Análisis de nodos para circuitos con fuentes de voltaje dependientes. Circuitos eléctricos.

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta