Introducción

Los voltajes de nodos son los parámetros en el análisis de nodos, y se emplea la LKC para determinarlos. Mientras que el análisis de lazos utiliza la LKV para determinar las corrientes en el circuito. Una vez que se conocen las corrientes, se puede aplicar la ley de Ohm para calcular los voltajes. Cuando un circuito incluye N lazos independientes, se necesitarán N ecuaciones simultáneas independientes para describir esta red.

Desarrollo del análisis de nodos

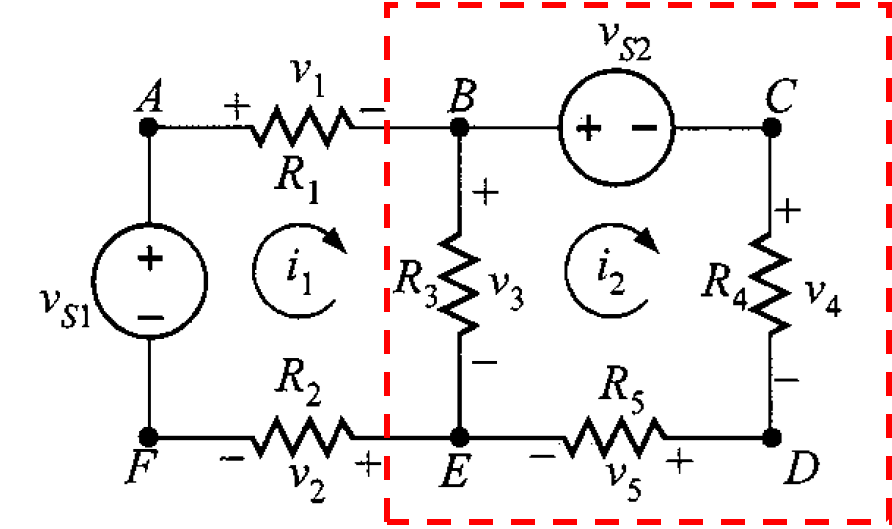
Para comenzar el análisis, se considera el siguiente circuito de la figura 1. En el circuito se identifican dos lazos, A-B-E-F-A y B-C-D-E-B. Se define ahora un nuevo conjunto de variables de corriente denominadas corrientes de lazo, que pueden usarse para encontrar las corrientes físicas en el circuito. Suponiendo que la corriente i_1 fluye en el primer lazo, y que i_2 lo hace en el segundo. Así, i_1 - i_2 es la corriente de rama que fluye de B a E a través de R_3. También se han supuesto las direcciones de las corrientes. Si las corrientes reales no fluyen en las direcciones que se indican, los valores calculados serán negativos.

Figura 1. Circuito ilustrativo.

Además, en este circuito se observa que v_1 = R_1 i_1, v_3 = R_3 (i_1 - i_2), v_4 = R_4 i_2, v_5 = R_5 i_2 y v_2 = R_2 i_1.

Aplicando la LKV al primer lazo se obtiene

\displaystyle \sum_{j=1}^n{v_n} = 0

\displaystyle -v_{s1} + v_1 + v_3 + v_2 = 0

\displaystyle - v_{s1} + R_1 i_1 + R_3 (i_1-i_2) + R_2 i_1 = 0

\displaystyle -v_{s1} + R_1 i_1 + R_3 i_1 - R_3 i_2 + R_2 i_1 = 0

\displaystyle (R_1 + R_2 + R_3) i_1 - R_3 i_2 = v_{s1}

Figura 2. Señalando el primer lazo para el análisis de LKV.

Y utilizando LKV para el segundo lazo produce

\displaystyle \sum_{j=1}^n{v_n} = 0

\displaystyle -v_3 + v_{s2} + v_4 + v_5 = 0

\displaystyle -R_3 (i_1 - i_2) + v_{s2} + R_4 i_2 + R_5 i_2 = 0

\displaystyle -R_3 i_1 + R_3 i_2 + v_{s2} + R_4 i_2 + R_5 i_2 = 0

\displaystyle -R_3 i_1 + (R_3 + R_4 + R_5) i_2 = - v_{s2}

Figura 3. Señalando el segundo lazo para el análisis de LKV.

Así que tomando todas el ecuaciones desarrolladas, se tiene el siguiente sistema

\displaystyle (R_1 + R_2 + R_3) i_1 - R_3 i_2 = v_{s1}
\displaystyle -R_3 i_1 + (R_3 + R_4 + R_5) i_2 = - v_{s2}

Expresándolo en forma matricial

\displaystyle \left[ \begin{matrix} (R_1 + R_2 + R_3) & - R_3 \\ - R_3 & (R_3 + R_4 + R_5) \end{matrix} \right] \left[ \begin{matrix} i_1 \\ i_2 \end{matrix} \right] = \left[ \begin{matrix} v_{s1} \\ - v_{s2} \end{matrix} \right]

Mostrando en forma general

\displaystyle \bold{R} \bold{I} = \bold{V}

Despejando \bold{I}

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

Esto significa que se debe hallar la inversa de \bold{R}, que se obtiene calculando su determinante y su matriz adjunta traspuesta.

Para tres nodos, la determinante de \bold{R} es

\displaystyle \text{det} \ \bold{R} = |\bold{R}|

\displaystyle \text{det} \ \bold{R} = \left|\begin{matrix} R_{11} & R_{12} \\ R_{21} & R_{22} \end{matrix} \right|

\displaystyle \text{det} \ \bold{R} = R_{11} R_{22} - R_{21} R_{12}

La matriz adjunta de \bold{R} se calcula como

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right]

donde C_{ij} es el cofactor correspondiente y se calcula utilizando la fórmula

\displaystyle C_{ij} = {(-1)}^{i+j} \ M_{ij}

donde M_{ij} es el menor del elemento R_{ij} y para encontrar el valor de cada menor, se realiza lo siguiente

\displaystyle M_{11} = \left|\begin{matrix} \bold{R_{11}} & \bold{R_{12}} \\ \bold{R_{21}} & R_{22} \end{matrix} \right| = R_{22}\displaystyle M_{12} = \left|\begin{matrix} \bold{R_{11}} & \bold{R_{12}} \\ R_{21} & \bold{R_{22}} \end{matrix} \right| = R_{21}
\displaystyle M_{21} = \left|\begin{matrix} \bold{R_{11}} & R_{12} \\ \bold{R_{21}} & \bold{R_{22}} \end{matrix} \right| = R_{12}\displaystyle M_{22} = \left|\begin{matrix} R_{11} & \bold{R_{12}} \\ \bold{R_{21}} & \bold{R_{22}} \end{matrix} \right| = R_{11}

Teniendo los resultados de cada menor, se puede calcular cada cofactor

\displaystyle C_{11} = {(-1)}^{1+1} M_{11} = R_{22}\displaystyle C_{12} = {(-1)}^{1+2} M_{12} = - R_{21}
\displaystyle C_{21} = {(-1)}^{2+1} M_{21} = - R_{12}\displaystyle C_{22} = {(-1)}^{2+2} M_{22} = R_{11}

Así, ya es posible conocer el resultado de la matriz adjunta de \bold{R}

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right] = \left[\begin{matrix} R_{22} & - R_{21} \\ - R_{12} & R_{11} \end{matrix} \right]

Una vez calculada la matriz adjunta, puede determinarse su traspuesta.

\displaystyle {(Adj \ \bold{R})}^T = \left[\begin{matrix} R_{22} & - R_{12} \\ - R_{21} & R_{11} \end{matrix} \right]

Teniendo los resultados de su matriz adjunta traspuesta y de su determinante, es posible determinar su inversa

\displaystyle \bold{R}^{-1} = \frac{{(Adj \ \bold{R})}^T}{\text{det} \ \bold{R}} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {(Adj \ \bold{R})}^T

Posteriormente, realizando la multiplicación matricial, es posible encontrar los valores de las incógnitas i_1 e i_2.

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

\displaystyle \bold{I} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {(Adj \ \bold{R})}^T \bold{V}

\displaystyle \left[ \begin{matrix} i_{1} \\ i_{2} \end{matrix} \right] = \left(\frac{1}{\text{det} \ \bold{R}} \right) \left[\begin{matrix} R_{22} & - R_{12} \\ - R_{21} & R_{11} \end{matrix} \right] \left[ \begin{matrix} v_{1} \\ v_{2} \end{matrix} \right]

\displaystyle \left[ \begin{matrix} i_{1} \\ i_{2} \end{matrix} \right] = \left(\frac{1}{R_{11} R_{22} - R_{21} R_{12}} \right) \left[\begin{matrix} R_{22} & - R_{12} \\ - R_{21} & R_{11} \end{matrix} \right] \left[ \begin{matrix} v_{s1} \\ - v_{s2} \end{matrix} \right]

\displaystyle \left[ \begin{matrix} i_{1} \\ i_{2} \end{matrix} \right] = \left[\frac{1}{(R_1 + R_2 + R_3) (R_3 + R_4 + R_5) - R_3 R_3} \right] \left[\begin{matrix} (R_3 + R_4 + R_5) & R_{3} \\ R_{3} & (R_1 + R_2 + R_3) \end{matrix} \right] \left[ \begin{matrix} v_{s1} \\ - v_{s2} \end{matrix} \right]

Realizando los cálculos necesarios (sustitución de valores y multiplicación matricial), se obtiene los valores de las corrientes i_1 e i_2.

¿Qué pasaría si el circuito mostrara cuatro nodos?

Si el circuito tuviera cuatro nodos, se realiza los siguiente: el determinante de \bold{R} es

\displaystyle \text{det} \ \bold{R} = |\bold{R}|

\displaystyle \text{det} \ \bold{R} = \left|\begin{matrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{matrix} \right|

\displaystyle \text{det} \ \bold{R} = \left(R_{11} R_{22} R_{33} + R_{12} R_{23} R_{31} + R_{13} R_{21} R_{32} \right) - \left(R_{31} R_{22} R_{13} + R_{32} R_{23} R_{11} + R_{33} R_{21} R_{12} \right)

La matriz adjunta de \bold{R} se calcula como

\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right]

donde C_{ij} es el cofactor correspondiente y se calcula utilizando la fórmula

\displaystyle C_{ij} = {(-1)}^{i+j} \ M_{ij}

donde M_{ij} es el menor del elemento R_{ij} y para encontrar el valor de cada menor, se realiza lo siguiente

\displaystyle M_{11} = \left|\begin{matrix} \bold{R_{11}} & \bold{R_{12}} & \bold{R_{13}} \\ \bold{R_{21}} & R_{22} & R_{23} \\ \bold{R_{31}} & R_{32} & R_{33} \end{matrix} \right| = \left|\begin{matrix} R_{22} & R_{23} \\ R_{32} & R_{33} \end{matrix} \right|\displaystyle M_{12} = \left|\begin{matrix} \bold{R_{11}} & \bold{R_{12}} & \bold{R_{13}} \\ R_{21} & \bold{R_{22}} & R_{23} \\ R_{31} & \bold{R_{32}} & R_{33} \end{matrix} \right| = \left|\begin{matrix} R_{21} & R_{23} \\ R_{31} & R_{33} \end{matrix} \right|\displaystyle M_{13} = \left|\begin{matrix} \bold{R_{11}} & \bold{R_{12}} & \bold{R_{13}} \\ R_{21} & R_{22} & \bold{R_{23}} \\ R_{31} & R_{32} & \bold{R_{33}} \end{matrix} \right| = \left|\begin{matrix} R_{21} & R_{22} \\ R_{31} & R_{32} \end{matrix} \right|
\displaystyle M_{21} = \left|\begin{matrix} \bold{R_{11}} & R_{12} & R_{13} \\ \bold{R_{21}} & \bold{R_{22}} & \bold{R_{23}} \\ \bold{R_{31}} & R_{32} & R_{33} \end{matrix} \right| = \left|\begin{matrix} R_{12} & R_{13} \\ R_{32} & R_{33} \end{matrix} \right|\displaystyle M_{22} = \left|\begin{matrix} R_{11} & \bold{R_{12}} & R_{13} \\ \bold{R_{21}} & \bold{R_{22}} & \bold{R_{23}} \\ R_{31} & \bold{R_{32}} & R_{33} \end{matrix} \right| = \left|\begin{matrix} R_{11} & R_{13} \\ R_{31} & R_{33} \end{matrix} \right|\displaystyle M_{23} = \left|\begin{matrix} R_{11} & R_{12} & \bold{R_{13}} \\ \bold{R_{21}} & \bold{R_{22}} & \bold{R_{23}} \\ R_{31} & R_{32} & \bold{R_{33}} \end{matrix} \right| = \left|\begin{matrix} R_{11} & R_{12} \\ R_{31} & R_{32} \end{matrix} \right|
\displaystyle M_{31} = \left|\begin{matrix} \bold{R_{11}} & R_{12} & R_{13} \\ \bold{R_{21}} & R_{22} & R_{23} \\ \bold{R_{31}} & \bold{R_{32}} & \bold{R_{33}} \end{matrix} \right| = \left|\begin{matrix} R_{12} & R_{13} \\ R_{22} & R_{23} \end{matrix} \right|\displaystyle M_{32} = \left|\begin{matrix} R_{11} & \bold{R_{12}} & R_{13} \\ R_{21} & \bold{R_{22}} & R_{23} \\ \bold{R_{31}} & \bold{R_{32}} & \bold{R_{33}} \end{matrix} \right| = \left|\begin{matrix} R_{11} & R_{13} \\ R_{21} & R_{23} \end{matrix} \right|\displaystyle M_{33} = \left|\begin{matrix} R_{11} & R_{12} & \bold{R_{13}} \\ R_{21} & R_{22} & \bold{R_{23}} \\ \bold{R_{31}} & \bold{R_{32}} & \bold{R_{33}} \end{matrix} \right| = \left|\begin{matrix} R_{11} & R_{12} \\ R_{21} & R_{22} \end{matrix} \right|

Teniendo los resultados de cada menor, se puede calcular cada cofactor

\displaystyle C_{11} = {(-1)}^{1+1} M_{11} = M_{11}\displaystyle C_{12} = {(-1)}^{1+2} M_{12} = - M_{12}\displaystyle C_{13} = {(-1)}^{1+3} M_{13} = M_{13}
\displaystyle C_{21} = {(-1)}^{2+1} M_{21} = - M_{21}\displaystyle C_{22} = {(-1)}^{2+2} M_{22} = M_{22}\displaystyle C_{23} = {(-1)}^{2+3} M_{23} = - M_{23}
\displaystyle C_{31} = {(-1)}^{3+1} M_{31} = M_{31}\displaystyle C_{32} = {(-1)}^{3+2} M_{32} = - M_{32}\displaystyle C_{33} = {(-1)}^{3+3} M_{33} = M_{33}

Nota. El determinante de cada menor no fue desarrollado ya que genera varios términos; sólo se expresará cuando se resuelva un problema donde implique matrices de 3×3.

Así, ya es posible conocer el resultado de la matriz adjunta de \bold{R}

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right] = \left[\begin{matrix} M_{11} & - M_{12} & M_{13} \\ - M_{21} & M_{22} &- M_{23} \\ M_{31} & - M_{32} & M_{33} \end{matrix} \right]

Una vez calculada la matriz adjunta, puede determinarse su traspuesta.

\displaystyle {(Adj \ \bold{R})}^T = \left[\begin{matrix} M_{11} & - M_{21} & M_{31} \\ - M_{12} & M_{22} &- M_{32} \\ M_{13} & - M_{23} & M_{33} \end{matrix} \right]

Teniendo los resultados de su matriz adjunta traspuesta y de su determinante, es posible determinar su inversa

\displaystyle \bold{R}^{-1} = \frac{{(Adj \ \bold{R})}^T}{\text{det} \ \bold{R}} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {(Adj \ \bold{R})}^T

Posteriormente, realizando la multiplicación matricial, es posible encontrar los valores de las incógnitas i_1, i_2 e i_3.

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

\displaystyle \bold{I} = \frac{{(Adj \ \bold{R})}^T}{\text{det} \ \bold{R}} \bold{V} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {(Adj \ \bold{R})}^T \bold{V}

\displaystyle \left[\begin{matrix} i_1 \\ i_2 \\ i_3 \end{matrix} \right] = \left(\frac{1}{\text{det} \ \bold{R}} \right) \left[\begin{matrix} M_{11} & - M_{21} & M_{31} \\ - M_{12} & M_{22} &- M_{32} \\ M_{13} & - M_{23} & M_{33} \end{matrix} \right] \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right]

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.