Problemas resueltos

Problema 1. Considere el circuito de la figura 1. Se desea encontrar la corriente I_o.

Figura 1. Circuito del problema 1.

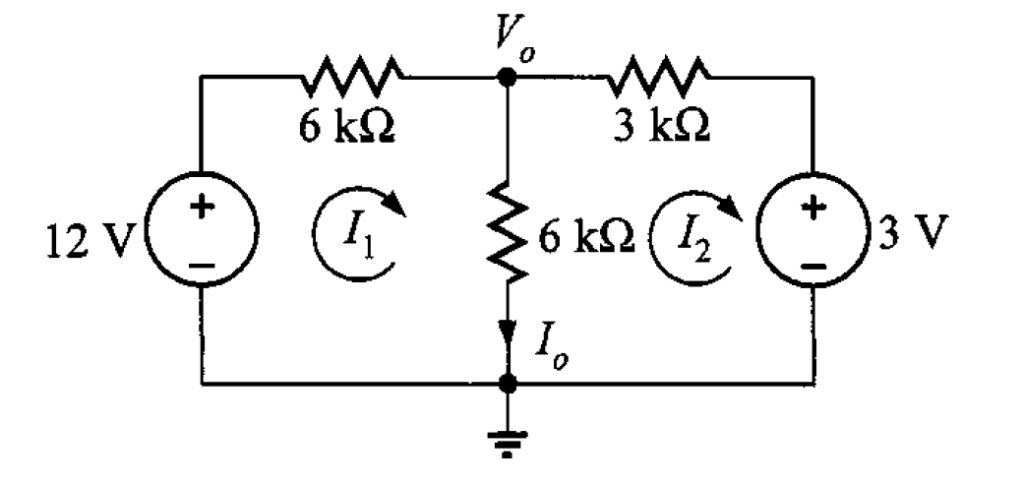
Primer método

Solución. Se desarrollará el análisis escribiendo las ecuaciones de malla. Se observa que no hay signos «+» y «-» en los resistores. Sin embargo, no son necesarios, ya que se aplicará la ley de Ohm a cada elemento resistivo al momento de escribir las ecuaciones de LKV. La ecuación para la primera malla es

\displaystyle \sum_{j=1}^n{V_j} = 0

\displaystyle -12 + (6 \text{k}) I_1 + (6 \ \text{k}) (I_1 - I_2) = 0

\displaystyle -12 + (6 \text{k}) I_1 + (6 \ \text{k}) I_1 - (6 \ \text{k}) I_2 = 0

\displaystyle (12 \ \text{k}) I_1 - (6 \ \text{k}) I_2 = 12

Figura 2. Señalando el primer lazo para el análisis de LKV.

Y aplicando LKV en la segunda malla resulta

\displaystyle \sum_{j=1}^n{V_j} = 0

\displaystyle - (6 \text{k}) (I_1 - I_2) + (3 \ \text{k}) I_2 + 3 = 0

\displaystyle - (6 \text{k}) I_1 + (6 \ \text{k}) I_2 + (3 \ \text{k}) I_2 + 3 = 0

\displaystyle - (6 \ \text{k}) I_1 + (9 \ \text{k}) I_2 = - 3

Figura 3. Señalando el segundo lazo para el análisis de LKV.

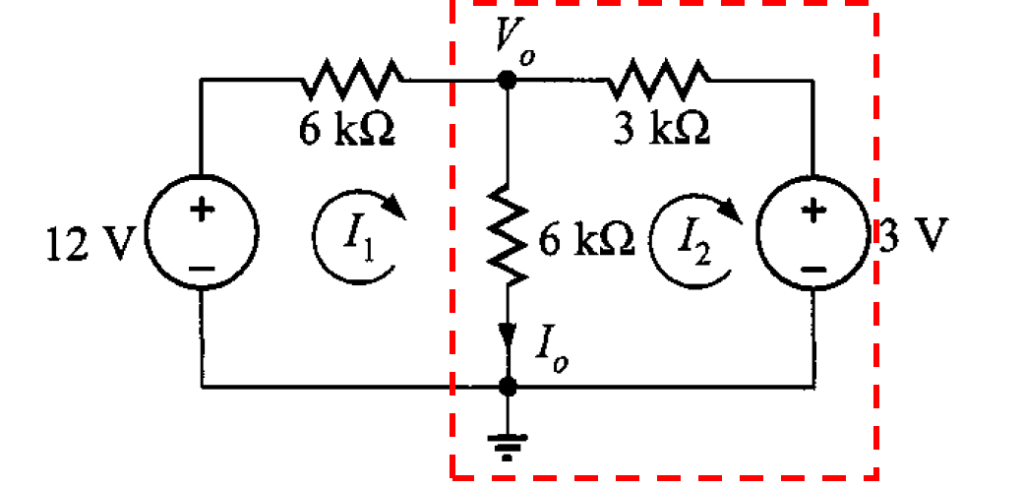
Tomando las ecuaciones desarrolladas, se tiene el sistema

\displaystyle (12 \ \text{k}) I_1 - (6 \ \text{k}) I_2 = 12
\displaystyle - (6 \ \text{k}) I_1 + (9 \ \text{k}) I_2 = - 3

Expresándolo en forma matricial

\displaystyle \left[ \begin{matrix} 12 \ \text{k} & - 6 \ \text{k} \\ - 6 \ \text{k} & 9 \ \text{k} \end{matrix} \right] \left[ \begin{matrix} I_1 \\ I_2 \end{matrix} \right] = \left[ \begin{matrix} 12 \\ - 3 \end{matrix} \right]

Mostrando en forma general

\displaystyle \bold{R} \bold{I} = \bold{V}

Despejando \bold{I}

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

Esto significa que se debe hallar la inversa de \bold{R}, que se obtiene calculando su determinante y su matriz adjunta traspuesta.

Como este circuito cuenta con tres nodos, la determinante de \bold{R} se calcula de la siguiente manera

\displaystyle \text{det} \ \bold{R} = |\bold{R}|

\displaystyle \text{det} \ \bold{R} = \left|\begin{matrix} 12 \ \text{k} & - 6 \ \text{k} \\ - 6 \ \text{k} & 9 \ \text{k} \end{matrix} \right|

\displaystyle \text{det} \ \bold{R} = \left(12 \ \text{k} \right) \left(9 \ \text{k} \right) - \left(-6 \ \text{k} \right) \left(-6 \ \text{k} \right)

\displaystyle \text{det} \ \bold{R} = 108 \ \text{k}^2 - 36 \ \text{k}^2

\displaystyle \text{det} \ \bold{R} = 72 \ \text{k}^2

La matriz adjunta de \bold{R} se calcula como

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right]

donde C_{ij} es el cofactor correspondiente y se calcula utilizando la fórmula

\displaystyle C_{ij} = {(-1)}^{i+j} \ M_{ij}

donde M_{ij} es el menor del elemento R_{ij} y para encontrar el valor de cada menor, se realiza lo siguiente

\displaystyle M_{11} = 9 \ \text{k}\displaystyle M_{12} = - 6 \ \text{k}
\displaystyle M_{21} = - 6 \ \text{k}\displaystyle M_{22} = 12 \ \text{k}

Teniendo los resultados de cada menor, se puede calcular cada cofactor

\displaystyle C_{11} = {(-1)}^{1+1} M_{11} = 9 \ \text{k}\displaystyle C_{12} = {(-1)}^{1+2} M_{12} = 6 \ \text{k}
\displaystyle C_{21} = {(-1)}^{2+1} M_{21} = 6 \ \text{k}\displaystyle C_{22} = {(-1)}^{2+2} M_{22} = 12 \ \text{k}

Así, ya es posible conocer el resultado de la matriz adjunta de \bold{R}

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right] = \left[\begin{matrix} 9 \ \text{k} & 6 \ \text{k} \\ 6 \ \text{k} & 12 \ \text{k} \end{matrix} \right]

Una vez calculada la matriz adjunta, puede determinarse su traspuesta.

\displaystyle {(Adj \ \bold{R})}^T = \left[\begin{matrix} 9 \ \text{k} & 6 \ \text{k} \\ 6 \ \text{k} & 12 \ \text{k} \end{matrix} \right]

Teniendo los resultados de su matriz adjunta traspuesta y de su determinante, es posible determinar su inversa

\displaystyle \bold{R}^{-1} = \frac{{(Adj \ \bold{R})}^T}{\text{det} \ \bold{R}} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {(Adj \ \bold{R})}^T

\displaystyle \bold{R}^{-1} = \left(\frac{1}{72 \ \text{k}^2} \right) \left[\begin{matrix} 9 \ \text{k} & 6 \ \text{k} \\ 6 \ \text{k} & 12 \ \text{k} \end{matrix} \right] = \left[\begin{matrix} \left(\frac{1}{72 \ \text{k}^2} \right) (9 \ \text{k}) & \left(\frac{1}{72 \ \text{k}^2} \right) (6 \ \text{k}) \\ \\ \left(\frac{1}{72 \ \text{k}^2} \right) (6 \ \text{k}) & \left(\frac{1}{72 \ \text{k}^2} \right) (12 \ \text{k}) \end{matrix} \right]

\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \frac{9}{72 \ \text{k}} & \frac{6}{72 \ \text{k}} \\ \\ \frac{6}{72 \ \text{k}} & \frac{12}{72 \ \text{k}} \end{matrix} \right] = \left[\begin{matrix} \frac{9}{72 \times 10^3} & \frac{6}{72 \times 10^3} \\ \\ \frac{6}{72 \times 10^3} & \frac{12}{72 \times 10^3} \end{matrix} \right]

\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \frac{1}{8} \times 10^{-3} & \frac{1}{12} \times 10^{-3} \\ \\ \frac{1}{12} \times 10^{-3} & \frac{1}{6} \times 10^{-3} \end{matrix} \right]

Posteriormente, sustituyendo y realizando la multiplicación matricial, es posible encontrar los valores de I_1 e I_2.

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \frac{1}{8} \times 10^{-3} & \frac{1}{12} \times 10^{-3} \\ \\ \frac{1}{12} \times 10^{-3} & \frac{1}{6} \times 10^{-3} \end{matrix} \right] \left[ \begin{matrix} 12 \\ -3 \end{matrix}\right]

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \left(\frac{1}{8} \times 10^{-3} \right)(12) + \left(\frac{1}{12} \times 10^{-3} \right)(-3) \\ \\ \left( \frac{1}{12} \times 10^{-3}\right)(12) + \left(\frac{1}{6} \times 10^{-3} \right)(-3) \end{matrix} \right]

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \frac{12}{8} \times 10^{-3} - \frac{3}{12} \times 10^{-3} \\ \\ \frac{12}{12} \times 10^{-3} - \frac{3}{6} \times 10^{-3} \end{matrix} \right] = \left[\begin{matrix} \frac{6}{4} \times 10^{-3} - \frac{1}{4} \times 10^{-3} \\ \\ \frac{2}{2} \times 10^{-3} - \frac{1}{2} \times 10^{-3} \end{matrix} \right]

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \frac{5}{4} \times 10^{-3} \\ \\ \frac{1}{2} \times 10^{-3} \end{matrix} \right] = \left[\begin{matrix} \frac{5}{4} \\ \\ \frac{1}{2} \end{matrix} \right] \times 10^{-3}

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \frac{5}{4} \\ \\ \frac{1}{2} \end{matrix} \right] \text{mA}

Las corrientes hallas son \displaystyle I_1 = \frac{5}{4} \ \text{mA} y \displaystyle I_2 = \frac{1}{2} \ \text{mA}. El valor de I_o es

\displaystyle \sum_{j=1}^n{I_j} = 0

\displaystyle - I_1 + I_2 + I_o = 0

\displaystyle I_o = I_1 - I_2

\displaystyle I_o = \frac{5}{4} \ \text{m} - \frac{1}{2} \ \text{m}

\displaystyle \therefore I_o = \frac{3}{4} \ \text{mA}

Segundo método

Dado que se desea calcular la corriente I_o, se puede aplicar el análsiis de lazos como se muestra en la figura 4.

Figura 4. Análisis de lazos para determinar Io.

Se observa que la corriente de lazo I_1 pasa por el tramo central de la red y, por lo tanto, I_1 = I_o. Aplicando la LKV en le primer lazo, su ecuación es

\displaystyle \sum_{j=1}^n{V_j} = 0

\displaystyle - 12 + (6 \ \text{k}) (I_1 + I_2) + (6 \ \text{k}) I_1 = 0

\displaystyle - 12 + (6 \ \text{k}) I_1 + (6 \ \text{k}) I_2 + (6 \ \text{k}) I_1 = 0

\displaystyle (12 \ \text{k}) I_1 + (6 \ \text{k}) I_1 = 12

Figura 5. Análisis del primer lazo para aplicar LKV.

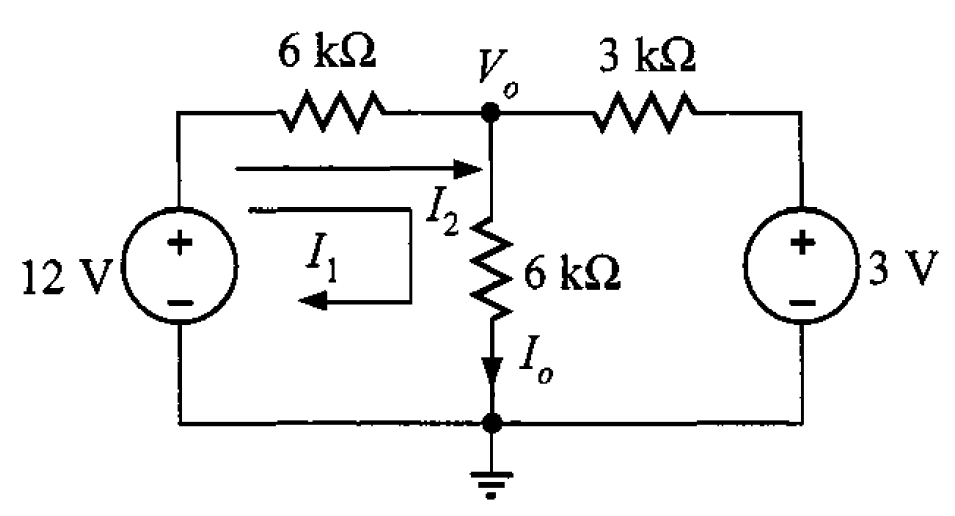
Y para el segundo lazo

\displaystyle \sum_{j=1}^n{V_j} = 0

\displaystyle - 12 + (6 \ \text{k}) (I_1 + I_2) + (3 \ \text{k}) I_2 + 3 = 0

\displaystyle - 12 + (6 \ \text{k}) I_1 + (6 \ \text{k}) I_2 + (3 \ \text{k}) I_2 + 3= 0

\displaystyle (6 \ \text{k}) I_1 + (9 \ \text{k}) I_1 = 9

Figura 6. Análisis del segundo lazo para aplicar LKV.

Tomando las ecuaciones desarrolladas, se tiene el sistema

\displaystyle (12 \ \text{k}) I_1 + (6 \ \text{k}) I_1 = 12
\displaystyle (6 \ \text{k}) I_1 + (9 \ \text{k}) I_1 = 9

Expresándolo en forma matricial

\displaystyle \left[ \begin{matrix} 12 \ \text{k} & 6 \ \text{k} \\ 6 \ \text{k} & 9 \ \text{k} \end{matrix} \right] \left[ \begin{matrix} I_1 \\ I_2 \end{matrix} \right] = \left[ \begin{matrix} 12 \\ 9 \end{matrix} \right]

Mostrando en forma general

\displaystyle \bold{R} \bold{I} = \bold{V}

Despejando \bold{I}

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

Esto significa que se debe hallar la inversa de \bold{R}, que se obtiene calculando su determinante y su matriz adjunta traspuesta.

Como este circuito cuenta con tres nodos, la determinante de \bold{R} se calcula de la siguiente manera

\displaystyle \text{det} \ \bold{R} = |\bold{R}|

\displaystyle \text{det} \ \bold{R} = \left|\begin{matrix} 12 \ \text{k} & 6 \ \text{k} \\ 6 \ \text{k} & 9 \ \text{k} \end{matrix} \right|

\displaystyle \text{det} \ \bold{R} = \left(12 \ \text{k} \right) \left(9 \ \text{k} \right) - \left(6 \ \text{k} \right) \left(6 \ \text{k} \right)

\displaystyle \text{det} \ \bold{R} = 108 \ \text{k}^2 - 36 \ \text{k}^2

\displaystyle \text{det} \ \bold{R} = 72 \ \text{k}^2

La matriz adjunta de \bold{R} se calcula como

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right]

donde C_{ij} es el cofactor correspondiente y se calcula utilizando la fórmula

\displaystyle C_{ij} = {(-1)}^{i+j} \ M_{ij}

donde M_{ij} es el menor del elemento R_{ij} y para encontrar el valor de cada menor, se realiza lo siguiente

\displaystyle M_{11} = 9 \ \text{k}\displaystyle M_{12} = 6 \ \text{k}
\displaystyle M_{21} = 6 \ \text{k}\displaystyle M_{22} = 12 \ \text{k}

Teniendo los resultados de cada menor, se puede calcular cada cofactor

\displaystyle C_{11} = {(-1)}^{1+1} M_{11} = 9 \ \text{k}\displaystyle C_{12} = {(-1)}^{1+2} M_{12} = - 6 \ \text{k}
\displaystyle C_{21} = {(-1)}^{2+1} M_{21} = - 6 \ \text{k}\displaystyle C_{22} = {(-1)}^{2+2} M_{22} = 12 \ \text{k}

Así, ya es posible conocer el resultado de la matriz adjunta de \bold{R}

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right] = \left[\begin{matrix} 9 \ \text{k} & - 6 \ \text{k} \\ - 6 \ \text{k} & 12 \ \text{k} \end{matrix} \right]

Una vez calculada la matriz adjunta, puede determinarse su traspuesta.

\displaystyle {(Adj \ \bold{R})}^T = \left[\begin{matrix} 9 \ \text{k} & - 6 \ \text{k} \\ - 6 \ \text{k} & 12 \ \text{k} \end{matrix} \right]

Teniendo los resultados de su matriz adjunta traspuesta y de su determinante, es posible determinar su inversa

\displaystyle \bold{R}^{-1} = \frac{{(Adj \ \bold{R})}^T}{\text{det} \ \bold{R}} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {(Adj \ \bold{R})}^T

\displaystyle \bold{R}^{-1} = \left(\frac{1}{72 \ \text{k}^2} \right) \left[\begin{matrix} 9 \ \text{k} & - 6 \ \text{k} \\ - 6 \ \text{k} & 12 \ \text{k} \end{matrix} \right] = \left[\begin{matrix} \left(\frac{1}{72 \ \text{k}^2} \right) (9 \ \text{k}) & \left(\frac{1}{72 \ \text{k}^2} \right) (-6 \ \text{k}) \\ \\ \left(\frac{1}{72 \ \text{k}^2} \right) (-6 \ \text{k}) & \left(\frac{1}{72 \ \text{k}^2} \right) (12 \ \text{k}) \end{matrix} \right]

\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \frac{9}{72 \ \text{k}} & - \frac{6}{72 \ \text{k}} \\ \\ - \frac{6}{72 \ \text{k}} & \frac{12}{72 \ \text{k}} \end{matrix} \right] = \left[\begin{matrix} \frac{9}{72 \times 10^3} & - \frac{6}{72 \times 10^3} \\ \\ - \frac{6}{72 \times 10^3} & \frac{12}{72 \times 10^3} \end{matrix} \right]

\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \frac{1}{8} \times 10^{-3} & - \frac{1}{12} \times 10^{-3} \\ \\ - \frac{1}{12} \times 10^{-3} & \frac{1}{6} \times 10^{-3} \end{matrix} \right]

Posteriormente, sustituyendo y realizando la multiplicación matricial, es posible encontrar los valores de I_1 e I_2.

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \frac{1}{8} \times 10^{-3} & - \frac{1}{12} \times 10^{-3} \\ \\ - \frac{1}{12} \times 10^{-3} & \frac{1}{6} \times 10^{-3} \end{matrix} \right] \left[ \begin{matrix} 12 \\ 9 \end{matrix}\right]

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \left(\frac{1}{8} \times 10^{-3} \right)(12) - \left(\frac{1}{12} \times 10^{-3} \right)(9) \\ \\ - \left( \frac{1}{12} \times 10^{-3}\right)(12) + \left(\frac{1}{6} \times 10^{-3} \right)(9) \end{matrix} \right]

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \frac{12}{8} \times 10^{-3} - \frac{9}{12} \times 10^{-3} \\ \\ - \frac{12}{12} \times 10^{-3} + \frac{9}{6} \times 10^{-3} \end{matrix} \right] = \left[\begin{matrix} \frac{18}{24} \times 10^{-3} \\ \\ \frac{6}{12} \times 10^{-3} \end{matrix} \right]

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \frac{3}{4} \times 10^{-3} \\ \\ \frac{1}{2} \times 10^{-3} \end{matrix} \right] = \left[\begin{matrix} \frac{3}{4} \\ \\ \frac{1}{2} \end{matrix} \right] \times 10^{-3}

\displaystyle \left[ \begin{matrix} I_1 \\ I_2 \end{matrix}\right] = \left[\begin{matrix} \frac{3}{4} \\ \\ \frac{1}{2} \end{matrix} \right] \text{mA}

Las corrientes hallas son \displaystyle I_1 = \frac{3}{4} \ \text{mA} y \displaystyle I_2 = \frac{1}{2} \ \text{mA}. El valor de I_o es

I_o = I_1

\therefore I_o =\frac{3}{4} \ \text{mA}

Problema 2. Resolver las corrientes de malla que se muestra en el circuito de la figura 6.

Figura 6. Circuito del problema 2.

Solución. Se tiene el siguiente análisis

Figura 7. Indicando las corrientes de malla del circuito del problema 2.

En el primer lazo, al utilizar la LKV, se tiene la ecuación siguiente

\displaystyle \sum_{j=1}^n{V_j} = 0

\displaystyle 6 + (4 \ \text{k}) I_1 + (6 \ \text{k})(I_1 - I_3) = 0

\displaystyle 6 + (4 \ \text{k}) I_1 + (6 \ \text{k}) I_1 - (6 \ \text{k}) I_3 = 0

\displaystyle (10 \ \text{k}) I_1 - (6 \ \text{k}) I_3 = -6

Figura 8. Señalando al primer lazo para aplicar la LKV.

En el segundo lazo, se obtiene la siguiente ecuación

\displaystyle \sum_{j=1}^n{V_j} = 0

\displaystyle (9 \ \text{k}) I_2 - 6 + (3 \ \text{k})(I_2 - I_3) = 0

\displaystyle (9 \ \text{k}) I_2 - 6 + (3 \ \text{k}) I_2 - (3 \ \text{k}) I_3 = 0

\displaystyle (12 \ \text{k}) I_2 - (3 \ \text{k}) I_3 = 6

Figura 9. Señalando al segundo lazo para aplicar la LKV.

Y en el tercer lazo

\displaystyle \sum_{j=1}^n{V_j} = 0

\displaystyle (3 \ \text{k}) (I_3 - I_2) + (6 \ \text{k})(I_3 - I_1) + (12 \ \text{k}) I_3 = 0

\displaystyle (3 \ \text{k}) I_3 - (3 \ \text{k}) I_2 + (6 \ \text{k}) I_3 - (6 \ \text{k}) I_1 + (12 \ \text{k}) I_3 = 0

\displaystyle - (6 \ \text{k}) I_1 - (3 \ \text{k}) I_2 + (21 \ \text{k}) I_3 = 0

Figura 10. Señalando al tercer lazo para aplicar la LKV.

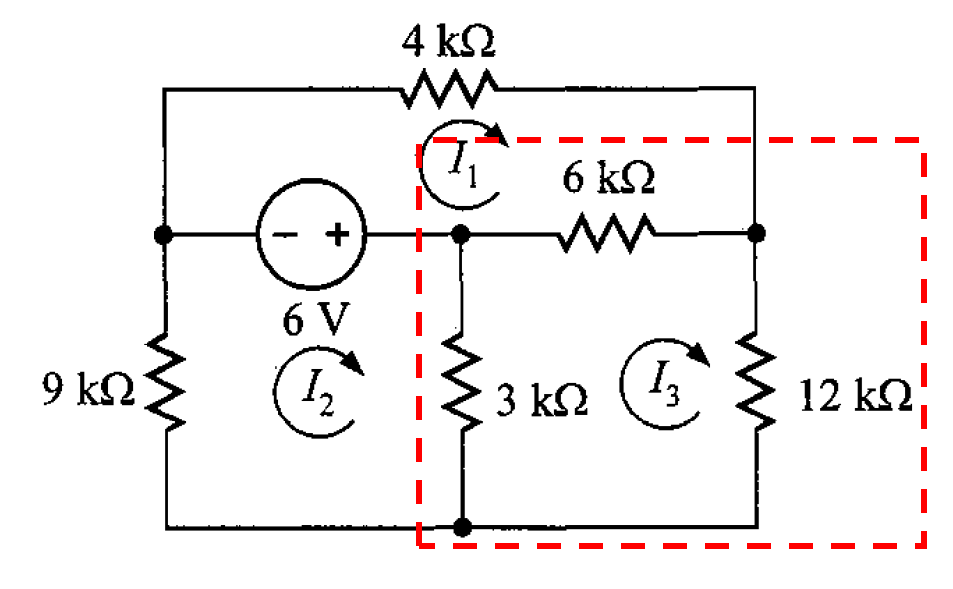
Tomando las ecuaciones calculadas, se tiene el siguiente sistema

\displaystyle (10 \ \text{k}) I_1 - (6 \ \text{k}) I_3 = -6
\displaystyle (12 \ \text{k}) I_2 - (3 \ \text{k}) I_3 = 6
\displaystyle - (6 \ \text{k}) I_1 - (3 \ \text{k}) I_2 + (21 \ \text{k}) I_3 = 0

Expresándolo en forma matricial

\displaystyle \left[ \begin{matrix} 10 \ \text{k} & 0 & 6 \ \text{k} \\ 0 & 12 \ \text{k} & - 3 \ \text{k} \\ - 6 \ \text{k} & - 3 \ \text{k} & 21 \ \text{k} \end{matrix} \right] \left[ \begin{matrix} I_1 \\ I_2 \\ I_3\end{matrix} \right] = \left[ \begin{matrix} -6 \\ 6 \\ 0 \end{matrix} \right]

Mostrando en forma general

\displaystyle \bold{R} \bold{I} = \bold{V}

Despejando \bold{I}

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

Esto significa que se debe hallar la inversa de \bold{R}, que se obtiene calculando su determinante y su matriz adjunta traspuesta. El determinante de \bold{R} es

\displaystyle \text{det} \ \bold{R} = |\bold{R}|

\displaystyle \text{det} \ \bold{R} = \left|\begin{matrix} 10 \ \text{k} & 0 & 6 \ \text{k} \\ 0 & 12 \ \text{k} & - 3 \ \text{k} \\ - 6 \ \text{k} & - 3 \ \text{k} & 21 \ \text{k} \end{matrix} \right|

\displaystyle \text{det} \ \bold{R} = 1998 \ \text{k}^3

La matriz adjunta de \bold{R} se calcula como

\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right]

donde C_{ij} es el cofactor correspondiente y se calcula utilizando la fórmula

\displaystyle C_{ij} = {(-1)}^{i+j} \ M_{ij}

donde M_{ij} es el menor del elemento R_{ij} y para encontrar el valor de cada menor, se realiza lo siguiente

\displaystyle M_{11} = \left|\begin{matrix}12 \ \text{k} & -3 \ \text{k} \\ -3 \ \text{k} & 21 \ \text{k} \end{matrix} \right| = 243 \ \text{k}^2\displaystyle M_{12} = \left|\begin{matrix} 0 & - 3\ \text{k} \\ -6 \ \text{k} & 21 \ \text{k} \end{matrix} \right| = - 18 \ \text{k}^2\displaystyle M_{13} = \left|\begin{matrix} 0 & 12 \ \text{k} \\ -6 \ \text{k} & -3 \ \text{k} \end{matrix} \right| = 72 \ \text{k}^2
\displaystyle M_{21} = \left|\begin{matrix} 0 & -6 \ \text{k} \\ -3 \ \text{k} & 21 \ \text{k} \end{matrix} \right| = - 18 \ \text{k}^2\displaystyle M_{22} = \left|\begin{matrix} 10 \ \text{k} & - 6 \ \text{k} \\ -6 \ \text{k} & 21 \ \text{k} \end{matrix} \right| = 174 \ \text{k}^2\displaystyle M_{23} = \left|\begin{matrix} 10 \ \text{k} & 0 \\ -6 \ \text{k} & -3 \ \text{k} \end{matrix} \right| = -30 \ \text{k}^2
\displaystyle M_{31} = \left|\begin{matrix} 0 & - 6 \ \text{k} \\ 12 \ \text{k} & -3 \ \text{k} \end{matrix} \right| = 72 \ \text{k}^2\displaystyle M_{32} = \left|\begin{matrix} 10 \ \text{k} & -6 \ \text{k} \\ 0 & -3 \ \text{k} \end{matrix} \right| = -30 \ \text{k}^2\displaystyle M_{33} = \left|\begin{matrix} 10 \ \text{k} & 0 \\ 0 \ \text{k} & 12 \ \text{k} \end{matrix} \right| = 120 \ \text{k}^2

Teniendo los resultados de cada menor, se puede calcular cada cofactor

\displaystyle C_{11} = M_{11} = 243 \ \text{k}^2\displaystyle C_{12} = - M_{12} = 18 \ \text{k}^2\displaystyle C_{13} = M_{13} = 72 \ \text{k}^2
\displaystyle C_{21} = - M_{21} = 18 \ \text{k}^2\displaystyle C_{22} = M_{22} = 174 \ \text{k}^2\displaystyle C_{23} = - M_{23} = 30 \ \text{k}^2
\displaystyle C_{31} = M_{31} = 72 \ \text{k}^2\displaystyle C_{32} = - M_{32} = 30 \ \text{k}^2\displaystyle C_{33} = M_{33} = 120 \ \text{k}^2

Así, ya es posible conocer el resultado de la matriz adjunta de \bold{R}

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right]

\displaystyle Adj \ \bold{R} = \left[\begin{matrix} 243 \ \text{k}^2 & 18 \ \text{k}^2 & 72 \ \text{k}^2 \\ 18 \ \text{k}^2 & 174 \ \text{k}^2 & 30 \ \text{k}^2 \\ 72 \ \text{k}^2 & 30 \ \text{k}^2 & 120 \ \text{k}^2 \end{matrix} \right]

Una vez calculada la matriz adjunta, puede determinarse su traspuesta.

\displaystyle {(Adj \ \bold{R})}^T = \left[\begin{matrix} 243 \ \text{k}^2 & 18 \ \text{k}^2 & 72 \ \text{k}^2 \\ 18 \ \text{k}^2 & 174 \ \text{k}^2 & 30 \ \text{k}^2 \\ 72 \ \text{k}^2 & 30 \ \text{k}^2 & 120 \ \text{k}^2 \end{matrix} \right]

Teniendo los resultados de su matriz adjunta traspuesta y de su determinante, es posible determinar su inversa

\displaystyle \bold{R}^{-1} = \frac{{(Adj \ \bold{R})}^T}{\text{det} \ \bold{R}} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {(Adj \ \bold{R})}^T

\displaystyle \bold{R}^{-1} = \left(\frac{1}{1998 \ \text{k}^3} \right) \left[\begin{matrix} 243 \ \text{k}^2 & 18 \ \text{k}^2 & 72 \ \text{k}^2 \\ 18 \ \text{k}^2 & 174 \ \text{k}^2 & 30 \ \text{k}^2 \\ 72 \ \text{k}^2 & 30 \ \text{k}^2 & 120 \ \text{k}^2 \end{matrix} \right]

\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \left(\frac{1}{1998 \ \text{k}^3} \right)(243 \ \text{k}^2) & \left(\frac{1}{1998 \ \text{k}^3} \right)(18 \ \text{k}^2) & \left(\frac{1}{1998 \ \text{k}^3} \right)(72 \ \text{k}^2) \\ \\ \left(\frac{1}{1998 \ \text{k}^3} \right)(18 \ \text{k}^2) & \left(\frac{1}{1998 \ \text{k}^3} \right)(174 \ \text{k}^2) & \left(\frac{1}{1998 \ \text{k}^3} \right)(30 \ \text{k}^2) \\ \\ \left(\frac{1}{1998 \ \text{k}^3} \right)(72 \ \text{k}^2) & \left(\frac{1}{1998 \ \text{k}^3} \right)(30 \ \text{k}^2) & \left(\frac{1}{1998 \ \text{k}^3} \right)(120 \ \text{k}^2) \end{matrix} \right]

\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \frac{243}{1998 \ \text{k}} & \frac{18}{1998 \ \text{k}} & \frac{72}{1998 \ \text{k}} \\ \\ \frac{18}{1998 \ \text{k}}& \frac{174}{1998 \ \text{k}} & \frac{30}{1998 \ \text{k}} \\ \\ \frac{72}{1998 \ \text{k}}& \frac{30}{1998 \ \text{k}} & \frac{120}{1998 \ \text{k}} \end{matrix} \right]

\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \frac{9}{74 \ \text{k}} & \frac{1}{111 \ \text{k}} & \frac{4}{111 \ \text{k}} \\ \\ \frac{1}{111 \ \text{k}}& \frac{29}{333 \ \text{k}} & \frac{5}{333 \ \text{k}} \\ \\ \frac{4}{111 \ \text{k}}& \frac{5}{333 \ \text{k}} & \frac{20}{333 \ \text{k}} \end{matrix} \right]

Posteriormente, realizando la multiplicación matricial, es posible encontrar los valores de las incógnitas I_1, I_2 e I_3.

\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}

\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \end{matrix} \right] = \left[\begin{matrix} \frac{9}{74 \ \text{k}} & \frac{1}{111 \ \text{k}} & \frac{4}{111 \ \text{k}} \\ \\ \frac{1}{111 \ \text{k}}& \frac{29}{333 \ \text{k}} & \frac{5}{333 \ \text{k}} \\ \\ \frac{4}{111 \ \text{k}}& \frac{5}{333 \ \text{k}} & \frac{20}{333 \ \text{k}} \end{matrix} \right] \left[\begin{matrix} -6 \\ 6 \\ 0 \end{matrix} \right]

\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \end{matrix} \right] = \left[\begin{matrix} \frac{9}{74 \times 10^{3}} & \frac{1}{111 \times 10^{3}} & \frac{4}{111 \times 10^{3}} \\ \\ \frac{1}{111 \times 10^{3}}& \frac{29}{333 \times 10^{3}} & \frac{5}{333 \times 10^{3}} \\ \\ \frac{4}{111\times 10^{3}}& \frac{5}{333 \times 10^{3}} & \frac{20}{333 \times 10^{3}} \end{matrix} \right] \left[\begin{matrix} -6 \\ 6 \\ 0 \end{matrix} \right]

\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \end{matrix} \right] = \left[\begin{matrix} \frac{9}{74} \times 10^{-3} & \frac{1}{111} \times 10^{-3} & \frac{4}{111} \times 10^{-3} \\ \\ \frac{1}{111} \times 10^{-3}& \frac{29}{333} \times 10^{-3} & \frac{5}{333} \times 10^{-3} \\ \\ \frac{4}{111}\times 10^{-3}& \frac{5}{333} \times 10^{-3} & \frac{20}{333} \times 10^{-3} \end{matrix} \right] \left[\begin{matrix} -6 \\ 6 \\ 0 \end{matrix} \right]

\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \end{matrix} \right] = \left[\begin{matrix} \left(\frac{9}{74} \times 10^{-3} \right) (-6) + \left(\frac{1}{111} \times 10^{-3} \right) (6) + \left(\frac{4}{111} \times 10^{-3} \right)(0) \\ \\ \left(\frac{1}{111} \times 10^{-3} \right) (-6) + \left(\frac{29}{333} \times 10^{-3} \right)(6) + \left(\frac{5}{333} \times 10^{-3} \right) (0) \\ \\ \left(\frac{4}{111}\times 10^{-3} \right) (-6) + \left(\frac{5}{333} \times 10^{-3} \right) (6) + \left(\frac{20}{333} \times 10^{-3} \right) (0) \end{matrix} \right]

\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \end{matrix} \right] = \left[\begin{matrix} - \frac{54}{74} \times 10^{-3} + \frac{6}{111} \times 10^{-3} + 0 \\ \\ - \frac{6}{111} \times 10^{-3} + \frac{174}{333} \times 10^{-3} +0 \\ \\ - \frac{24}{111}\times 10^{-3} + \frac{30}{333} \times 10^{-3} + 0 \end{matrix} \right] = \left[\begin{matrix} - \frac{25}{37} \times 10^{-3} \\ \\ \frac{52}{111} \times 10^{-3} \\ \\ - \frac{14}{111}\times 10^{-3} \end{matrix} \right]

\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \end{matrix} \right] = \left[\begin{matrix} - 0.676 \times 10^{-3} \\ 0.468 \times 10^{-3} \\ - 0.126\times 10^{-3} \end{matrix} \right] = \left[\begin{matrix} - 0.676 \\ 0.468 \\ - 0.126 \end{matrix} \right] \times 10^{-3}

\displaystyle \therefore \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \end{matrix} \right] = \left[\begin{matrix} - 0.676 \\ 0.468 \\ - 0.126 \end{matrix} \right] \ \text{mA}

Se concluye que I_1 = -0.676 \ \text{mA}, I_2 = 0.468 \ \text{mA} y I_3 = -0.126 \ \text{mA}.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.