Obtención de área planas por integración cuando la diferencial de área es una función cartesiana. Cálculo integral.

Introducción

El área entre una curva $y=f(x)$ , el eje de las $x$ y las ordenadas correspondientes $x=a$ y $x=b$ está dada por la fórmula

$\displaystyle \text{Area} = \int_a^b{y \, dx}$

La fórmula anterior es fácil de recordar, puesto que el elemento de área es un rectángulo como $BQ$ (figura 1) de base $dx$ y altura $y$ .

figura 4.4.1 — Figura 1. Representación gráfica del área.

El área buscada $ACRP$ es el límite de la suma de todos esos rectángulos (tiras) ubicados entre las ordenadas $AP$ y $CR$ .

Se aplica el teorema fundamental del cálculo integral al cálculo del área de la superficie limitada por la curva $x=\phi (y)$ , el eje de las $y$ y las líneas horizontales $y=c$ y $y = d$ .

Primer paso. Se construyen los $n$ rectángulos tal y como se indica en la figura 2.

figura 4.4.2 — Figura 2. Representación gráfica del área dividido en «n» rectángulos en el eje «x».

Naturalmente que el área buscada es el límite de la suma de las áreas de estos rectángulos cuando su número tiende a infinito y la altura de cada uno tiene a cero.

Segundo paso. Las alturas se representan con $\Delta y_1$ , $\Delta y_2$ , $\Delta y_3$ , etc. En cada intervalo, se toma un punto en la extremidad superior y se designa las ordenadas de dichos puntos como $y_1$ , $y_2$ , $y_3$ , etc. Por lo anterior, las bases son $\phi (y_1 )$ , $\phi (y_2 )$ , $\phi (y_3 )$ , etc. Por tanto, la suma de las áreas de los rectángulos es

$\displaystyle \phi (y_1 ) \Delta y_1 + \phi (y_2 ) \Delta y_2 + \phi (y_3 ) \Delta y_3 + \cdots + \phi (y_n ) \Delta y_n = \sum_{i=1}^{n}{\phi (y_i ) \Delta y_i}$

Tercer paso. Por el teorema fundamental del cálculo integral se obtiene:

$\displaystyle \lim_{n \rightarrow \infty}{\sum_{i=1}^{n}{\phi (y_i ) \Delta y_i} }= \int_c^d{\phi (y) \, dy}$

Entonces el área entre una curva dada, el eje de las $y$ y las líneas horizontales $y=c$ y $y=d$ está dada por la fórmula

$\displaystyle \text{Area} = \int_c^d{x \, dy}$

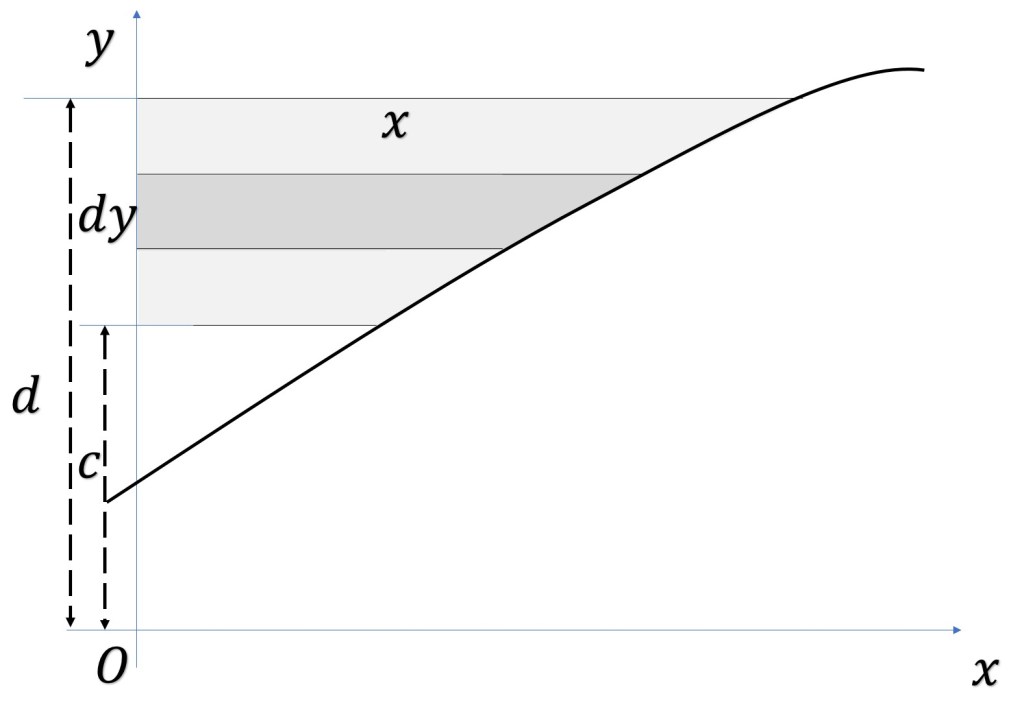
La fórmula anterior es fácil de recordar, si se piensa en el límite de la suma de todos los rectángulos horizontales (tiras) contenidos en el área buscada, ya que $x$ y $dy$ son la base y la altura, respectivamente, de un rectángulo cualquiera (figura 3).

figura 4.4.3 — Figura 3. Representación gráfica del área.

Problemas resueltos

Problema 1. Calcular el área de la superficie limitada por la curva $y = xe^x$ , el eje de las $x$ y la recta $x=4$ .

Solución. Tomando la fórmula para calcular el área sobre el eje $x$

$\displaystyle \text{Area} = \int_a^b{y \, dx} = \int_0^4{xe^x \, dx}$

Resolviéndolo como una integral

$\displaystyle \int_0^4{xe^x \, dx} \quad \rightarrow \quad \int{xe^x \, dx}$

Se aplica el método de integración por partes.

$\displaystyle \int{xe^x \, dx} = e^x (x-1) + C$

Regresando y reemplazando la variable x por sus respectivos límites

$\displaystyle \int_0^4{xe^x \, dx} = [e^x (x-1)+C]_0^4$

$\displaystyle \int_0^4{xe^x \, dx} = e^4 (4-1) - e^0 (0-1)$

$\displaystyle \int_0^4{xe^x \, dx} = e^{4} (3) - (1)(-1) = 3e^4+e^0$

Finalmente

$\displaystyle \text{Area} = \int_0^4{xe^x \, dx}$

$\displaystyle \text{Area} = 3e^4 + 1$

$\displaystyle \therefore \text{Area} = 3e^4 + 1 \ \text{u}^2 = 164.794 \ \text{u}^2$

Problema 2. Calcular el área de la superficie limitada por la curva $y = \ln{x}$ , el eje de las $x$ y la recta $x=10$ .

Solución. Se realiza una tabulación desde x=0 hasta x=10.

Graficando, se tiene lo siguiente

figura 4.4.4 — Figura 4. Representación gráfica de la función y=ln(x).

Después, calculando el área tomando la siguiente fórmula

$\displaystyle \text{Area} = \int_a^b{y \, dx} = \int_1^{10}{\ln{x} \, dx}$

Resolviéndolo como una integral indefinida

$\displaystyle \int_1^{10}{\ln{x} \, dx} \quad \rightarrow \quad \int{\ln{x} \, dx}$

Por el método de integración por partes, resulta

$\displaystyle \int{\ln{x} \, dx} = x \ln{x} - \int{dx} = x \ln{x} - x + C$

Regresando y reemplazando la variable $x$ por sus límites

$\displaystyle \int_1^{10}{\ln{x} \, dx} = [x \ln{x} - x + C]_1^{10}$

$\displaystyle \int_1^{10}{\ln{x} \, dx} = (10 \ln{10} - 10) - (1 \ln{1} - 1) = 14.026$

Finalmente

$\displaystyle \text{Area} = \int_1^{10}{\ln{x} \, dx}$

$\therefore \text{Area} = 14.026 \ \text{u}^2$

Problema 3. Calcular el área de la superficie limitada por la curva $x=9y-y^3$ , el eje de las $y$ y las rectas $y=0$ y $y=3$ .

Solución. Teniendo definidos los límites y la ecuación de la curva, se toma la fórmula para calcular el área bajo el eje $y$ .

$\displaystyle \text{Area} = \int_c^d{x \, dy} = \int_0^3{(9y - y^3 ) \, dy}$

Resolviéndolo como una integral

$\displaystyle \int_0^3{(9y - y^3 ) \, dy} \rightarrow \int{(9y-y^3 ) \, dy}$

Continuando

$\displaystyle \int{(9y-y^3 ) \, dy} = 9\int{y \, dy} - \int{y^3 \, dy}$

Ambas integrales son similares a

$\displaystyle \int{v^n \, dv} = \frac{1}{n+1} v^{n+1} + C$

Entonces

$\displaystyle \int{(9y-y^3 ) \, dy} = 9\left(\frac{1}{2 }y^2 + C \right) - \left(\frac{1}{4} y^4 + C\right) = \frac{9}{2} y^2 - \frac{1}{4} y^4 + C$

Regresando y reemplazando la variable $y$ por sus límites

$\displaystyle \int_0^3{(9y-y^3 ) \, dy} = \left[\frac{9}{2} y^2 - \frac{1}{4} y^4 + C\right]_0^3$

$\displaystyle \int_0^3{(9y-y^3 ) \, dy} = \left[\frac{9}{2} (3)^2 - \frac{1}{4} (3)^4 \right] - \left[\frac{9}{2} (0)^2 - \frac{1}{4} (0)^4 \right]$

$\displaystyle \int_0^3{(9y-y^3 ) \, dy} = \frac{81}{2} - \frac{81}{4} - 0 = \frac{81}{4}$

Finalmente

$\displaystyle \text{Area} = \int_0^3{(9y - y^3 ) \, dy}$

$\displaystyle \therefore \text{Area} = \frac{81}{4} \ \text{u}^2= 20.25 \ \text{u}^2$

Obtención de área planas por integración cuando la diferencial de área es una función cartesiana. Cálculo integral.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Obtención de área planas por integración cuando la diferencial de área es una función cartesiana. Cálculo integral.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta