Superposición. Circuitos eléctricos.

Introducción

El principio de superposición proporciona esta habilidad para reducir un problema complejo a varios problemas más simples, cada uno con una fuente independiente única, y establece que

«En cualquier circuito lineal con varias fuentes independientes, la corriente o el voltaje en cualquier punto de la red puede calcularse con la suma algebraica de las contribuciones individuales de cada fuente actuando sola.»

Cuando se determina la contribución de una fuente independiente, todas las fuentes de voltaje restantes se hacen cero reemplazándolas con un cortocircuito, mientras que todas las fuentes de corrientes restantes se hacen cero sustituyéndolas con un circuito abierto.

Aunque la superposición se puede aplicar en redes lineales con fuentes dependientes, esto no es útil porque la fuente dependiente nunca es cero.

La superposición es aplicable a un circuito con cualquier número de fuentes dependientes e independientes. Es una propiedad fundamental de las ecuaciones lineales y puede aplicarse a cualquier efecto que esté relacionado linealmente con su causa. A este respecto, es importante señalar que, aun cuando la superposición se aplica tanto a la corriente como al voltaje en un circuito linea, no puede usarse para determinar la potencia, ya que ésta no es una función lineal.

Problemas resueltos

Problema 1. Considerar el circuito de la figura 1, en donde no se especifican los valores reales de las fuentes de voltaje. Obtener las ecuaciones para $i_1 (t)$ y $i_2 (t)$ utilizando el principio de superposición.

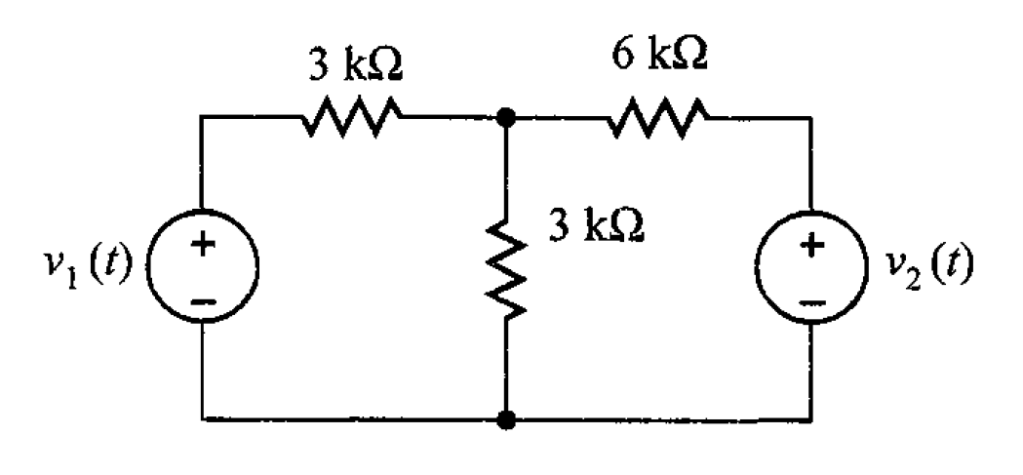
Solución. La superposición se aplica de la siguiente forma: $v_2 (t)$ debe ser cero para que únicamente actúe $v_1 (t)$ ; esto significa que la fuente $v_2 (t)$ es reemplazada por un cortocircuito (figura 2).

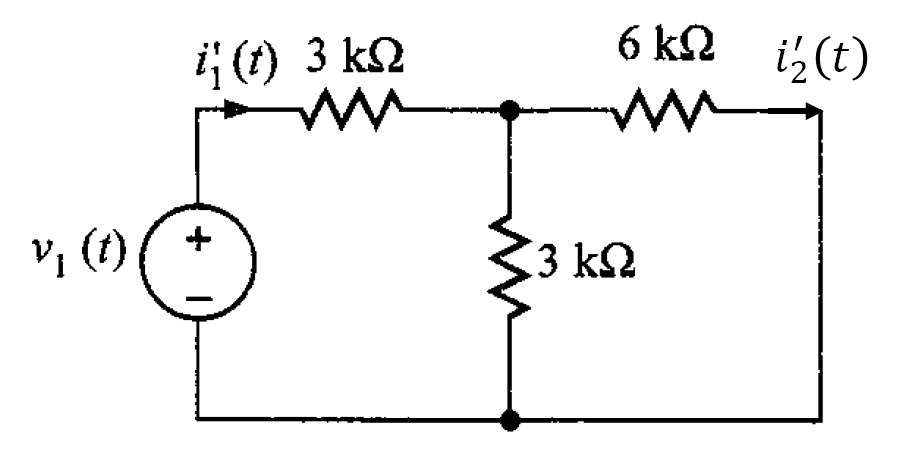
*Figura 2. Aplicando la primera parte de la superposición.*

Se emplea el circuito de la figura 2 para determinar el valor de $i_1 (t)$ producido sólo por $v_1 (t)$ , y este valor se denota $i'_1 (t)$ . Aplicando la ley de Ohm, resulta

$\displaystyle v_1 (t) = \left[3 \ \text{k} + \frac{(3 \ \text{k})(6 \ \text{k})}{3 \ \text{k} + 6 \ \text{k}} \right] i'_1 (t)$

$\displaystyle v_1 (t) = \left(3 \ \text{k} + 2 \text{k} \right) i'_1 (t) = \left(5 \ \text{k} \right) i'_1 (t)$

$\displaystyle i'_1 (t) = \frac{v_1 (t)}{5 \ \text{k}}$

Para obtener el valor de $i'_2 (t)$ , se utiliza el divisor de corriente

$\displaystyle i'_2 (t) = \left(\frac{3 \ \text{k}}{3 \ \text{k} + 6 \ \text{k}} \right) i'_1 (t)$

$\displaystyle i'_2 (t) = \left( \frac{3 \ \text{k}}{9 \ \text{k}} \right) i'_1 (t)$

$\displaystyle i'_2 (t) = \frac{1}{3} i'_1 (t)$

$\displaystyle i'_2 (t) = \frac{1}{3} \left[\frac{v_1 (t)}{5 \ \text{k}} \right]$

$\displaystyle i'_2 (t) = \frac{v_1 (t)}{15 \ \text{k}}$

Ahora, haciendo un cortocircuito en la fuente $v_2 (t)$ , es decir, $v_2 (t) = 0$ , se tiene el circuito de la figura 3.

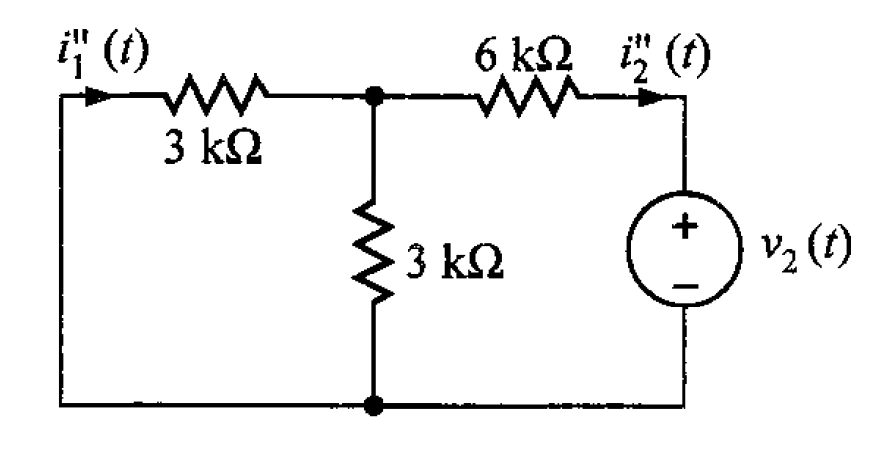
Figura 3. Aplicando la segunda parte de la superposición

Luego, aplicando la ley de Ohm, el valor de $i''_2(t)$ es

$\displaystyle v_2 (t) = - \left[6 \ \text{k} + \frac{(3 \ \text{k})(3 \ \text{k})}{3 \ \text{k} + 3 \ \text{k}} \right] i''_2 (t)$

$\displaystyle v_2 (t) = - \left(6 \ \text{k} + \frac{9}{6} \ \text{k} \right) i''_2 (t) = - \left(6 \ \text{k} + \frac{3}{2} \ \text{k} \right) i''_2 (t) = - \left(\frac{15}{2} \ \text{k} \right) i''_2 (t)$

$\displaystyle i''_2 (t) = - \frac{2 v_2 (t)}{15 \ \text{k}}$

Para obtener $i''_1 (t)$

$\displaystyle i''_1 (t) = \frac{3 \ \text{k}}{3 \ \text{k} + 3 \ \text{k}} i''_2 (t)$

$\displaystyle i''_1 (t) = \frac{3 \ \text{k}}{6 \ \text{k}} i''_2 (t) = \frac{1}{2} i''_2 (t)$

$\displaystyle i''_1 (t) = \frac{1}{2} \left[- \left(\frac{2}{15} \ \text{k} \right) v_2 (t) \right] = - \left(\frac{1}{15} \ \text{k} \right) v_2 (t)$

$\displaystyle i''_1 (t) = - \frac{v_2 (t)}{15 \ \text{k}}$

Finalmente, sumando los valores de $i'_1 (t)$ y de $i''_1 (t)$ , se obtiene el valor de $i_1 (t)$ .

$\displaystyle i_1 (t) = i'_1 (t) + i''_1 (t)$

$\displaystyle i_1 (t) = \frac{v_1 (t)}{5 \ \text{k}} + \left[- \frac{v_2 (t)}{15 \ \text{k}} \right]$

$\displaystyle i_1 (t) = \frac{v_1 (t)}{5 \ \text{k}} - \frac{v_2 (t)}{15 \ \text{k}}$

También se aplica el mismo procedimiento para obtener el resultado de $i_2 (t)$ .

$\displaystyle i_2 (t) = i'_2 (t) + i''_2 (t)$

$\displaystyle i_2 (t) = \frac{v_1 (t)}{15 \ \text{k}} + \left[- \frac{2v_2 (t)}{15} \ \text{k} \right]$

$\displaystyle i_2 (t) = \frac{v_1 (t)}{15 \ \text{k}} - \frac{2 v_2 (t)}{15} \ \text{k}$

En conclusión, se tienen las ecuaciones esperadas.

\displaystyle i_1 (t) = \frac{v_1 (t)}{5 \ \text{k}} - \frac{v_2 (t)}{15 \ \text{k}}

\displaystyle i_2 (t) = \frac{v_1 (t)}{15 \ \text{k}} - \frac{2 v_2 (t)}{15} \ \text{k}

Problema 2. Utilice la superposición para encontrar $V_o$ en el circuito de la figura 4.

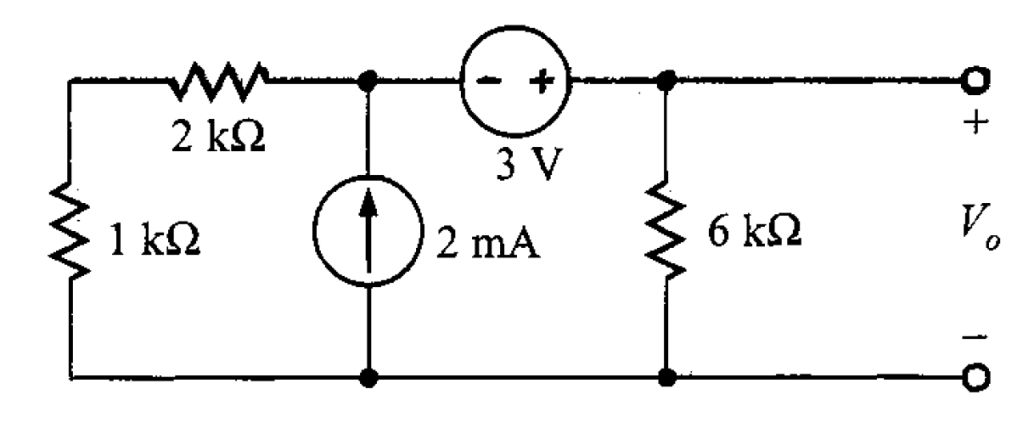
Solución. Para aplicar la superposición, primero se debe encontrar la contribución de la fuente de 2 mA en el voltaje de salida utilizando la división de corriente en la red de la figura 5 (haciendo que la fuente de voltaje actúe como un cortocircuito).

Figura 5. Circuito del problema 2 donde se ha hecho que la fuente de voltaje actúe como un cortocircuito.

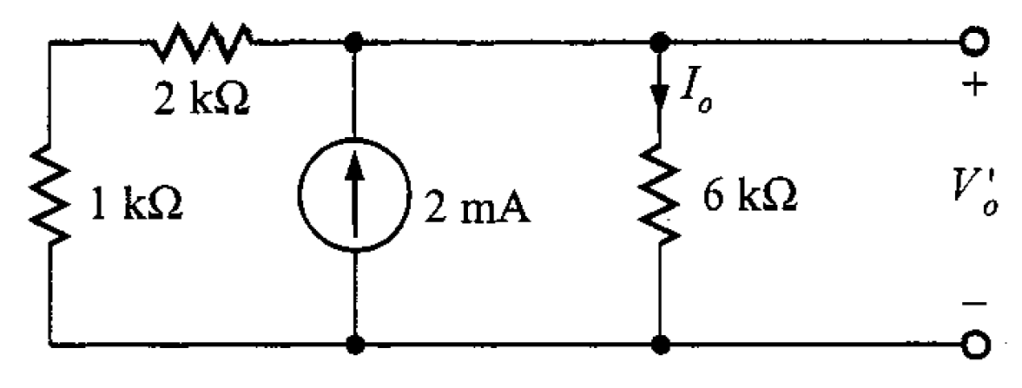
entonces

$\displaystyle I_o = \left[\frac{(2 \ \text{k} + 1 \ \text{k})}{(2 \ \text{k} + 1 \ \text{k}) + 6 \ \text{k}} \right] (2 \ \text{m})$

$\displaystyle I_o = \left(\frac{3}{9} \right) (2 \ \text{m}) = \left(\frac{1}{3} \right) (2 \ \text{m})$

$\displaystyle I_o = \frac{2}{3} \ \text{mA}$

Así, se sabe que el valor de $V'_o$ es

$\displaystyle V'_o = (6 \ \text{k}) I_o$

$\displaystyle V'_o = (6 \ \text{k}) \left(\frac{2}{3} \ \text{m} \right) = (6 \times 10^3) \left(\frac{2}{3} \times 10^{-3} \right) = \frac{12}{3}$

$\displaystyle V'_o = 4 \ \text{V}$

Ahora, se hace que la fuente de corriente se comporte como circuito abierto (figura 6).

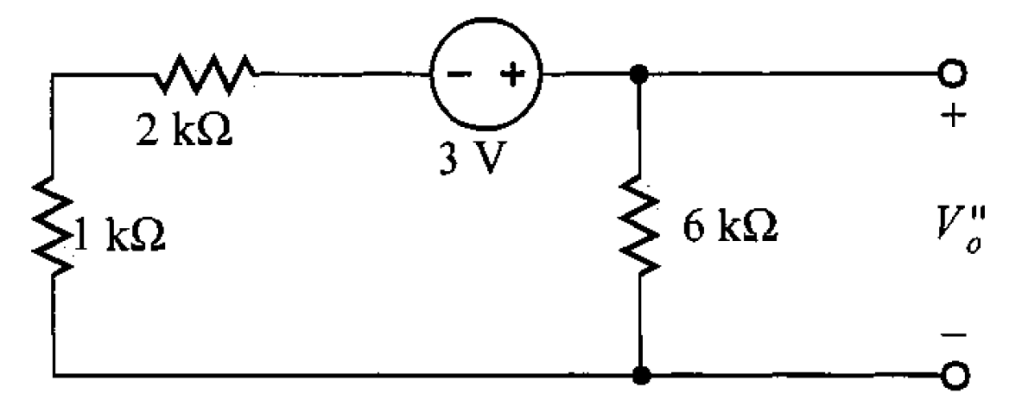
Figura 6. Circuito del problema 2 donde la fuente de corriente actúa como circuito abierto.

Para determinar el valor de $V''_o$ , solo basta con utilizar la división de voltaje.

$\displaystyle V''_o = \left[ \frac{6 \ \text{k}}{(2 \ \text{k} + 1 \ \text{k}) + 6 \ \text{k}} \right] (3)$

$\displaystyle V''_o = \left( \frac{6 \ \text{k}}{9 \ \text{k}} \right) (3)$

$\displaystyle V''_o =2 \ \text{V}$

Finalmente, sumando los resultados anterior, el valor de $V_o$ es

$\displaystyle V_o = V'_o + V''_o$

$\displaystyle V_o = 4 +2$

$\displaystyle \therefore V_o = 6 \ \text{V}$

Problema 3. Dada la siguiente red (figura 7), usar la superposición para calcular $V_o$ .

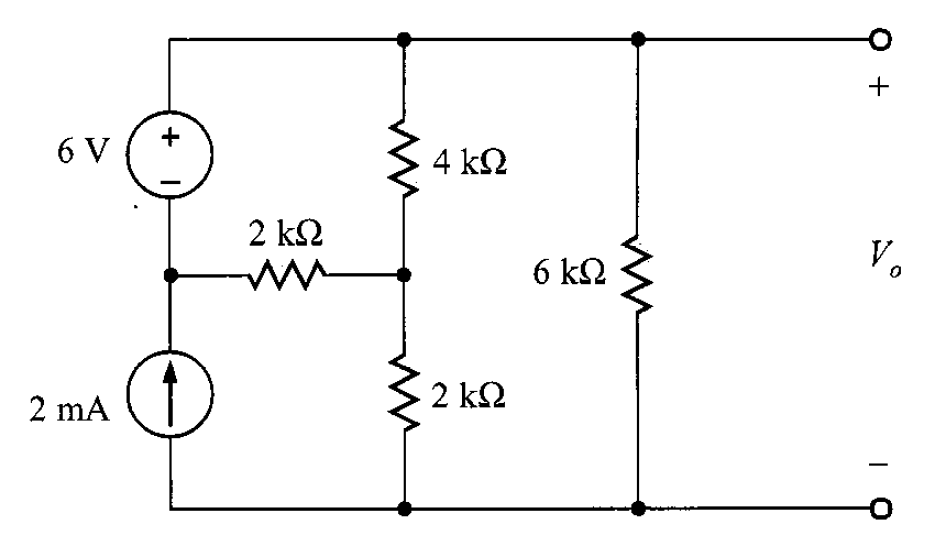
Solución. Para aplicar la superposición, primero se hace que la fuente de corriente se comporte como circuito abierto (figura 8), provocando la contribución de la fuente de 6 V a $V_o$ .

Figura 8. Fuente de corriente en circuito abierto.

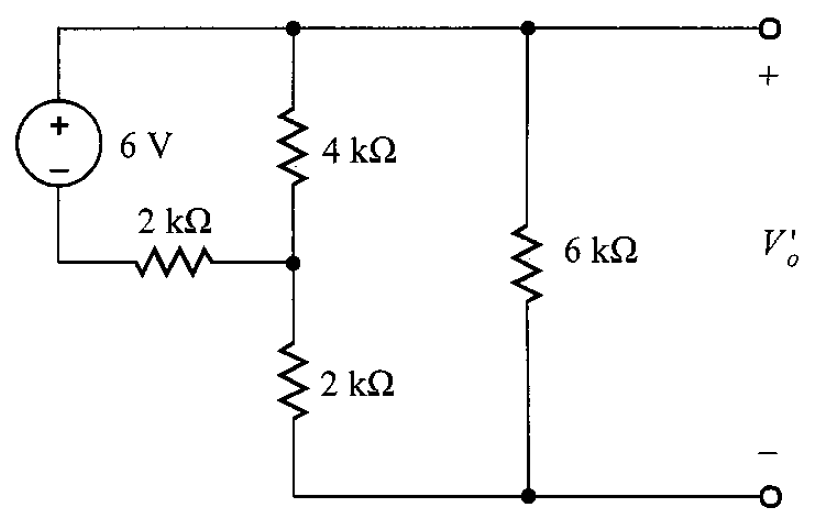
Realizando un acomodo en la red, se tiene que lo siguiente (figura 9)

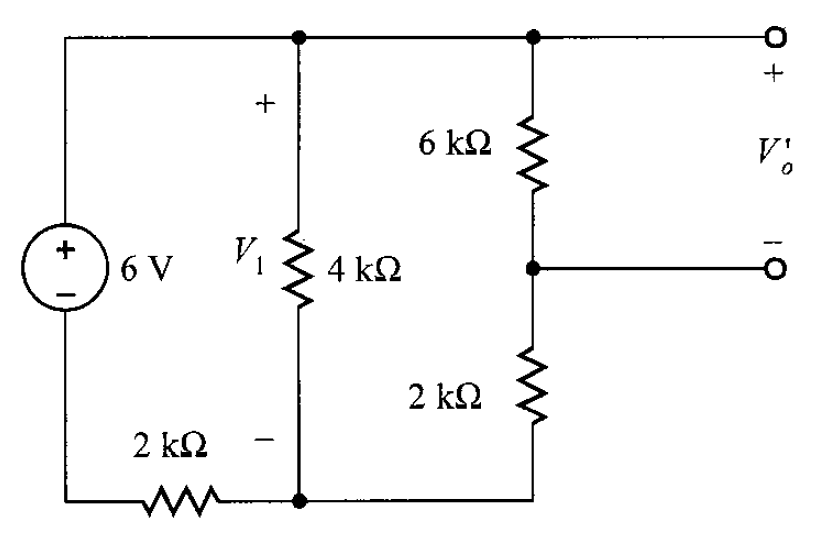
Después, se observa que los resistores de 2 kΩ y 6 kΩ están en serie y ambas están en paralelo con el resistor de 4 kΩ.

$\displaystyle R_{S1} = 2 \ \text{k} \Omega + 6 \ \text{k} \Omega = 8 \ \text{k} \Omega$

$\displaystyle \frac{1}{R_{P1}} = \frac{1}{4 \ \text{k} \Omega} + \frac{1}{R_{S1}} = \frac{1}{4 \ \text{k} \Omega} + \frac{1}{8 \ \text{k} \Omega} \rightarrow R_{P1} = \frac{8}{3} \ \text{k} \Omega$

Por división de voltaje se puede determinar $V_1$ y es

$\displaystyle V_1 = \left( \frac{\frac{8}{3} \ \text{k}}{2 \ \text{k} + \frac{8}{3} \ \text{k}} \right)$

$\displaystyle V_1 = \left(\frac{\frac{8}{3} \ \text{k}}{\frac{14}{3} \ \text{k}} \right) (6) = \frac{8}{14} (6) = \frac{48}{14}$

$\displaystyle V_1 = \frac{24}{7} \ \text{V}$

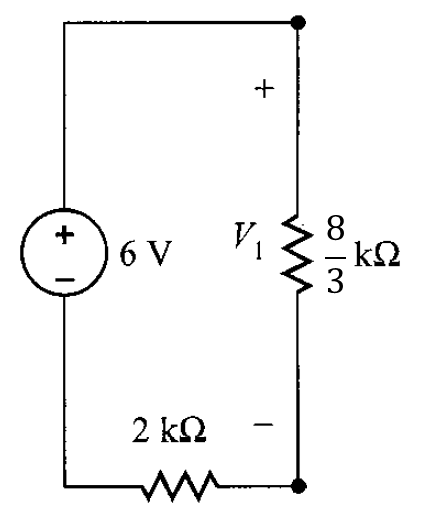
Con esto es posible calcular $V'_o$ .

$\displaystyle V'_o = \left(\frac{6 \ \text{k}}{6 \ \text{k} + 2 \ \text{k}} \right) V_1$

$\displaystyle V'_o = \left(\frac{6 \ \text{k}}{8 \ \text{k}} \right) V_1 = \frac{3}{4} V_1 = \frac{18}{7}$

$\displaystyle V'_o = \frac{18}{7} \ \text{V}$

Ahora, haciendo que la fuente de voltaje se comporte como un cortocircuito, se tiene el siguiente circuito (figura 11).

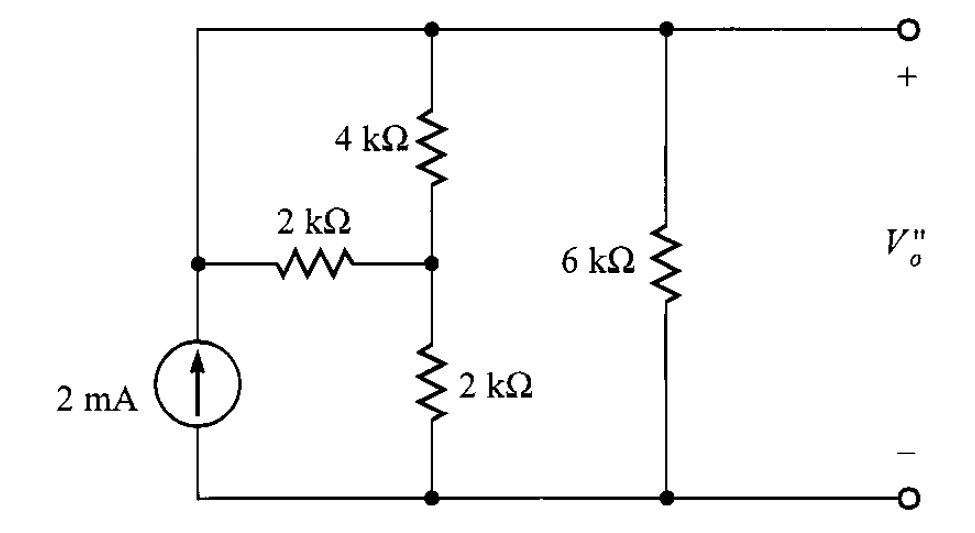
En la figura 11, se observa que los resistores de 2 kΩ y 4 kΩ están en paralelo; su resultado es

$\displaystyle \frac{1}{R_{P2}} = \frac{1}{2 \ \text{k}} + \frac{1}{4 \ \text{k}} \rightarrow R_{P2} = \frac{4}{3} \ \text{k} \Omega$

Reduciendo el circuito, en la figura 12 se muestra la siguiente modificación.

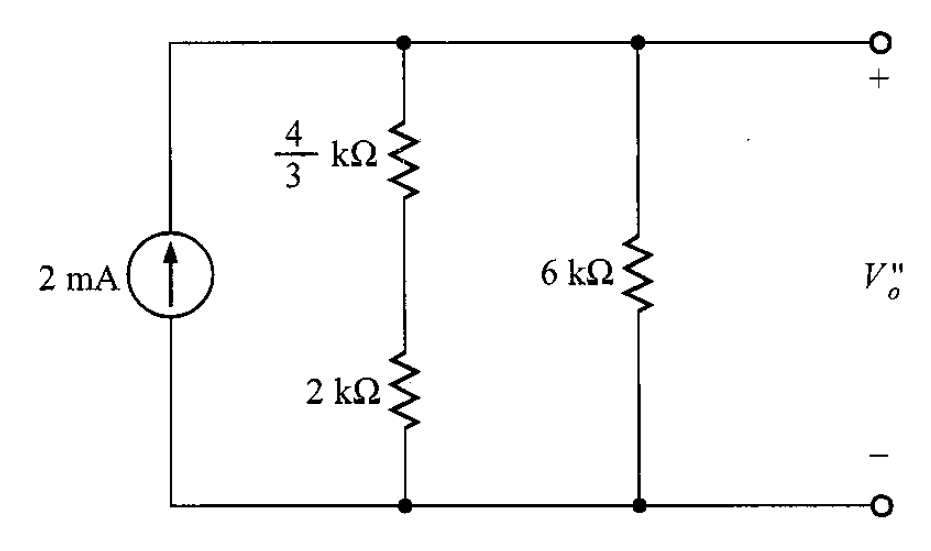
Figura 12. Circuito del problema 3 haciendo que la fuente de voltaje actúe como un cortocircuito.

En la figura 12 se observa que el voltaje $V''_o$ es el producto de la fuente de corriente y la combinación en paralelo de las resistencias de 4/3 kΩ y 2 kΩ con 6 kΩ. Entonces

$\displaystyle V''_o = \left[ \frac{(6 \ \text{k}) \left(\frac{4}{3} \ \text{k} + 2 \ \text{k} \right)}{\left(\frac{4}{3} \ \text{k} + 2 \ \text{k} \right) + 6 \ \text{k}} \right] (2 \ \text{m})$

$\displaystyle V''_o = \left[ \frac{(6 \ \text{k}) \left(\frac{10}{3} \ \text{k} \right)}{\left(\frac{4}{3} \ \text{k} + 2 \ \text{k} \right) + 6 \ \text{k}} \right] (2 \ \text{m}) = \left( \frac{\frac{60}{3} \ \text{k}^2}{\frac{28}{3} \ \text{k}} \right) (2 \ \text{m})$

$\displaystyle V''_o = \left( \frac{60}{28} \ \text{k} \right) (2 \ \text{m}) = \left( \frac{15}{7} \ \text{k} \right) (2 \ \text{m}) = \left( \frac{15}{7} \times 10^{3} \right) (2 \times 10^{-3}) = \frac{7}{14}$