Obteniendo la resistencia Thévenin en circuitos que incluyen únicamente fuentes dependientes. Circuitos eléctricos.

Problemas resueltos

Problema 1. Determinar el equivalente de Thévenin para la red de la figura 1 en las terminales A-B.

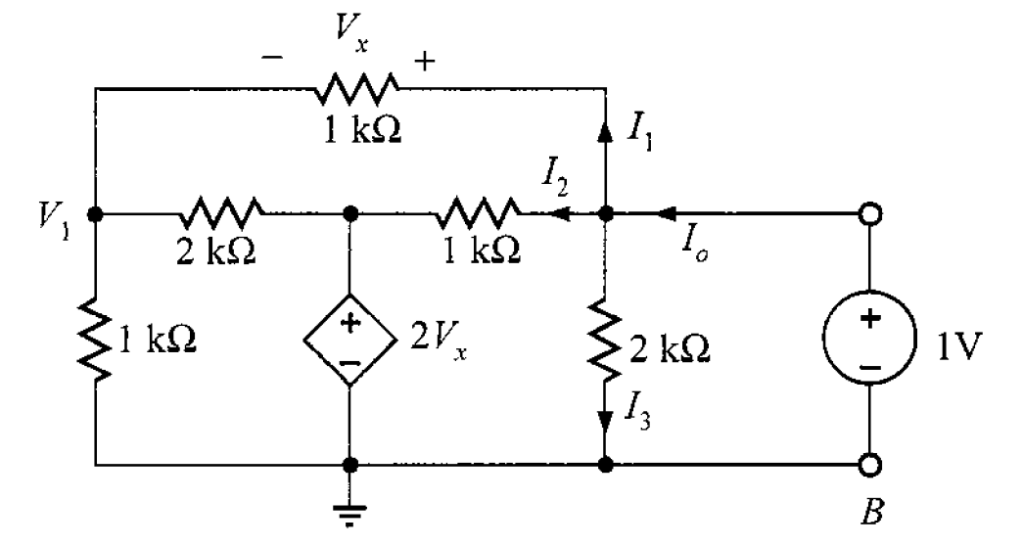
Solución. Para resolverlo, es necesario aplicar una fuente de voltaje independiente, cuyo valor sería de 1 V y que será conectado a las terminales A-B, provocando que $\displaystyle R_{\text{Th}} = \frac{1}{I_o}$ (figura 2).

Figura 2. Conectando una fuente de voltaje de 1 V en las terminales A-B.

En la figura 2, al aplicar LKV alrededor del lazo externo, se tiene que

$\displaystyle \sum_{j=1}^n{V_j} = 0$

$\displaystyle 1 - V_x - V_1 = 0$

$\displaystyle V_1 + V_x = 1$

Al usar LKC en el nodo $V_1$ , su ecuación es

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{V_1}{1 \ \text{k}} + \frac{V_1 - 2 V_x}{2 \ \text{k}} + \frac{V_1 - 1}{1 \ \text{k}} = 0$

$\displaystyle \frac{V_1}{1 \ \text{k}} + \frac{V_1}{2 \ \text{k}} - \frac{2 V_x}{2 \ \text{k}} + \frac{V_1}{1 \ \text{k}} - \frac{1}{1 \ \text{k}} = 0$

$\displaystyle \frac{5}{2 \ \text{k}} V_1 - \frac{V_x}{1 \ \text{k}} = \frac{1}{1 \ \text{k}}$

$\displaystyle 5V_1 - 2 V_x = 2$

Con las ecuaciones obtenidas, se tiene el siguiente conjunto

Expresándolo en forma matrical

$\displaystyle \left[\begin{matrix} 1 & 1 \\ 5 & - 2 \end{matrix} \right] \left[\begin{matrix} V_1 \\ V_x \end{matrix} \right] = \left[\begin{matrix} 1 \\ 2 \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} V_1 \\ V_x \end{matrix} \right] = {\left[\begin{matrix} 1 & 1 \\ 5 & -2 \end{matrix} \right]}^{-1} \left[\begin{matrix} 1 \\ 2 \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} V_1 \\ V_x \end{matrix} \right] = \left(-\frac{1}{7} \right) \left[\begin{matrix} - 2 & - 1 \\ \\ -5 & 1 \end{matrix} \right] \left[\begin{matrix} 1 \\ \\ 2 \end{matrix} \right] = \left[\begin{matrix} \left(-\frac{1}{7} \right) \left(- 2 \right) & \left(-\frac{1}{7} \right) \left(-1 \right) \\ \\ \left(-\frac{1}{7} \right) (-5) & \left(-\frac{1}{7} \right) (1) \end{matrix} \right] \left[\begin{matrix} 1 \\ \\ 2 \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} V_1 \\ V_x \end{matrix} \right] = \left[\begin{matrix} \frac{2}{7} & \frac{1}{7} \\ \\ \frac{5}{7} & - \frac{1}{7} \end{matrix} \right] \left[\begin{matrix} 1 \\ \\ 2 \end{matrix} \right] = \left[\begin{matrix} \left(\frac{2}{7}\right)(1) + \left(\frac{1}{7} \right) (2) \\ \\ \left(\frac{5}{7} \right)(1) + \left(- \frac{1}{7} \right)(2) \end{matrix} \right] = \left[\begin{matrix} \frac{2}{7} + \frac{2}{7} \\ \\ \frac{5}{7} - \frac{2}{7} \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} V_1 \\ V_x \end{matrix} \right] = \left[\begin{matrix} \frac{4}{7} \\ \\ \frac{3}{7} \end{matrix} \right] \ \text{V}$

Entonces, $\displaystyle V_1 = \frac{4}{7} \ \text{V}$ y $\displaystyle V_x = \frac{3}{7} \ \text{V}$ . Luego, se determinarán los valores de las corriente $I_1$ , $I_2$ e $I_3$ . La corriente $I_1$ es

$\displaystyle I_1 = \frac{V_x}{1 \ \text{k}}$

$\displaystyle I_1 = \frac{\frac{3}{7}}{1 \ \text{k}} = \frac{\frac{3}{7}}{1 \times 10^3} = \frac{3}{7} \times 10^{-3}$

$\displaystyle I_1 = \frac{3}{7} \ \text{mA}$

La corriente $I_2$ es

$\displaystyle I_2 = \frac{1 - 2 V_x}{1 \ \text{k}}$

$\displaystyle I_2 = \frac{1 - 2 \left(\frac{3}{7} \right)}{1 \ \text{k}} = \frac{\frac{1}{7}}{1 \ \text{k}} = \frac{\frac{1}{7}}{1 \times 10^3} = \frac{1}{7} \times 10^{-3}$

$\displaystyle I_2 = \frac{1}{7} \ \text{mA}$

Y la corriente $I_3$ es

$\displaystyle I_3 = \frac{1}{2 \ \text{k}}$

$\displaystyle I_3 = \frac{1}{2 \times 10^3} = \frac{1}{2} \times 10^{-3}$

$\displaystyle I_3 = \frac{1}{2} \ \text{mA}$

Por LKC, despejando $I_o$ , su valor es

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle -I_o + I_1 + I_2 + I_3 = 0$

$\displaystyle I_o = I_1 + I_2 + I_3$

$\displaystyle I_o = \frac{3}{7} \ \text{mA} + \frac{1}{7} \ \text{mA} + \frac{1}{2} \ \text{mA}$

$\displaystyle I_o = \frac{15}{14} \ \text{mA}$

Finalmente, la resistencia Thévenin es

$\displaystyle R_{\text{Th}} = \frac{1}{I_o}$

$\displaystyle R_{\text{Th}} = \frac{1}{\frac{15}{14} \ \text{m}} = \frac{1}{\frac{15}{14} \times 10^{-3}} = \frac{14}{15} \times 10^3$

$\displaystyle \therefore R_{\text{Th}} = \frac{14}{15} \ \text{k} \Omega$

Problema 2. Determine $R_{\text{Th}}$ en las terminales A-B de la red de la figura 3.

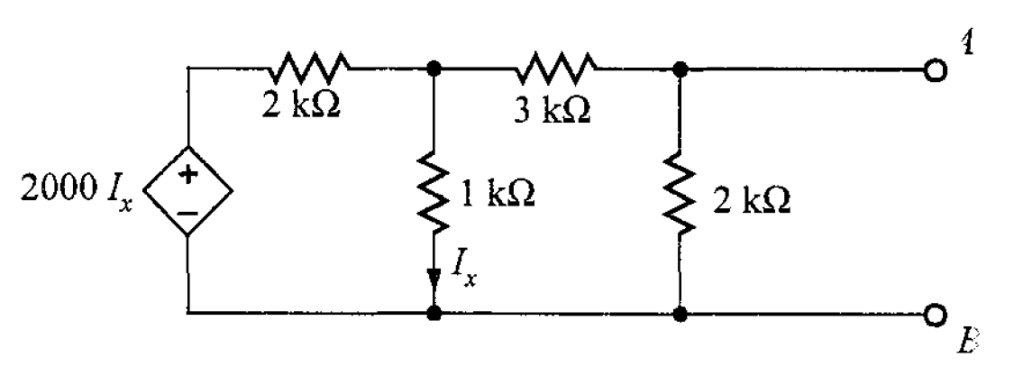
Solución. Para resolver este problema se conectará una fuente de corriente de 1 mA entre las terminales A-B, y con esto ayudará a calcular el voltaje de la terminal $V_2$ y posteriormente $R_{\text{Th}}$ (figura 4).

Figura 4. Conectando una fuente de corriente independiente de 1 mA en las terminales A-B.

Con la ayuda del análisis de nodos, se determinarán las ecuaciones de cada uno en los nodos 1 y 2. En el primer nodo, su ecuación es

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{V_1 - 2000 I_x}{2 \ \text{k}} + \frac{V_1 - V_2}{3 \ \text{k}} + \frac{V_1}{1 \ \text{k}} = 0$

$\displaystyle \frac{V_1}{2 \ \text{k}} - \frac{2000 I_x}{2 \ \text{k}} + \frac{V_1}{3 \ \text{k}} - \frac{V_2}{3 \ \text{k}} + \frac{V_1}{1 \ \text{k}} = 0$

$\displaystyle \frac{11}{6 \ \text{k}} V_1 - \frac{V_2}{3 \ \text{k}} - I_x = 0$

$\displaystyle 11 V_1 - 2 V_2 - (6 \ \text{k}) I_x = 0$

Y en el segundo nodo, su ecuación es

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{V_2 - V_1}{3 \ \text{k}} + \frac{V_2}{2 \ \text{k}} - 1 \ \text{m} = 0$

$\displaystyle \frac{V_2}{3 \ \text{k}} - \frac{V_1}{3 \ \text{k}} + \frac{V_2}{2 \ \text{k}} - 1 \ \text{m} = 0$

$\displaystyle - \frac{V_1}{3 \ \text{k}} + \frac{5}{6 \ \text{k}} V_2 = 1 \ \text{m}$

$\displaystyle - 2V_1 + 5 V_2 = 6$

La ecuación de restricción es

$\displaystyle I_x = \frac{V_1}{1 \ \text{k}}$

Con estas tres ecuaciones, se tiene el siguiente sistema

\displaystyle 11 V_1 - 2 V_2 - (6 \ \text{k}) I_x = 0

Sustituyendo la ecuación (3) en (1), el sistema de ecuaciones se reduce a dos ecuaciones

\displaystyle 11 V_1 - 2 V_2 - (6 \ \text{k}) \left(\frac{V_1}{1 \ \text{k}} \right) = 0

Simplificando

Expresándolo en forma matricial, resulta

$\displaystyle \left[\begin{matrix} 5 & -2 \\ -2 & 5 \end{matrix} \right] \left[\begin{matrix} V_1 \\ V_2 \end{matrix} \right] = \left[\begin{matrix} 0 \\ 6 \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} V_1 \\ V_2 \end{matrix} \right] = {\left[\begin{matrix} 5 & -2 \\ -2 & 5 \end{matrix} \right]}^{-1} \left[\begin{matrix} 0 \\ 6 \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} V_1 \\ V_2 \end{matrix} \right] = \left(\frac{1}{21} \right) \left[\begin{matrix} 5 & -2 \\ -2 & 5 \end{matrix} \right] \left[\begin{matrix} 0 \\ 6 \end{matrix} \right] = \left[\begin{matrix} \left(\frac{1}{21} \right) (5) & \left(\frac{1}{21} \right) (-2) \\ \\ \left(\frac{1}{21} \right) (-2) & \left(\frac{1}{21} \right) (5) \end{matrix} \right] \left[\begin{matrix} 0 \\ \\ 6 \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} V_1 \\ \\ V_2 \end{matrix} \right] = \left[\begin{matrix} \frac{5}{21} & - \frac{2}{21} \\ \\ - \frac{2}{21} & \frac{5}{21} \end{matrix} \right] \left[\begin{matrix} 0 \\ \\ 6 \end{matrix} \right] = \left[\begin{matrix} \left(\frac{5}{21} \right)(0) + \left(- \frac{2}{21} \right)(6) \\ \\ \left(- \frac{1}{21} \right)(0) + \left(\frac{5}{21} \right)(6) \end{matrix} \right] = \left[\begin{matrix} 0 - \frac{12}{21} \\ \\ 0 + \frac{30}{21} \end{matrix} \right] = \left[\begin{matrix} \frac{12}{21} \\ \\ \frac{30}{21} \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} V_1 \\ \\ V_2 \end{matrix} \right] = \left[\begin{matrix} \frac{4}{7} \\ \\ \frac{10}{7} \end{matrix} \right] \ \text{V}$

Así que $\displaystyle V_1 = \frac{4}{7} \ \text{V}$ y $\displaystyle V_2 = \frac{10}{7} \ \text{V}$ .

Finalmente,

$\displaystyle R_{\text{Th}} = \frac{V_2}{1 \ \text{mA}} = \frac{V_2}{1 \ \text{m}}$

$\displaystyle R_{\text{Th}} = \frac{\frac{10}{7}}{1 \ \text{m}} = \frac{\frac{10}{7}}{1 \times 10^{-3}} = \frac{10}{7} \times 10^{3}$

$\displaystyle \therefore R_{\text{Th}} = \frac{10}{7} \ \text{k} \Omega$

$\displaystyle 11 V_1 - 2 V_2 - (6 \ \text{k}) \left(\frac{V_1}{1 \ \text{k}} \right) = 0$	(1)
$\displaystyle - 2V_1 + 5 V_2 = 6$	(2)

$\displaystyle 5 V_1 - 2 V_2 = 0$	(1)
$\displaystyle - 2V_1 + 5 V_2 = 6$	(2)

Obteniendo la resistencia Thévenin en circuitos que incluyen únicamente fuentes dependientes. Circuitos eléctricos.

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Obteniendo la resistencia Thévenin en circuitos que incluyen únicamente fuentes dependientes. Circuitos eléctricos.

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta