Análisis de circuitos con amplificadores operacionales. Circuitos eléctricos.

Introducción

En un amplificador operacional ideal, $R_i$ y $A$ son infinitos y $R_o$ es cero. Por tanto, la corriente por las entradas inversora y no inversora es nula en el amplificador operacional, y si éste no está saturado, dichas entradas tienen el mismo voltaje. En este tema se supondrá que los amplificadores operacionales son lineales y funcionan en la zona lineal siempre que no se especifique lo contrario.

Problema resuelto

Problema 1. El amplificador operacional de la figura 1 es ideal y no está saturado. Calcular

a) $V_2 / V_1$
b) la resistencia de entrada $V_1/I_1$
c) $I_1$ , $I_2$ , $P_1$ (potencia suministrada por $V_1$ ) y $P_2$ (potencia disipada en las resistencias), suponiendo que $V_1 = 0.5 \ \text{V}$ .

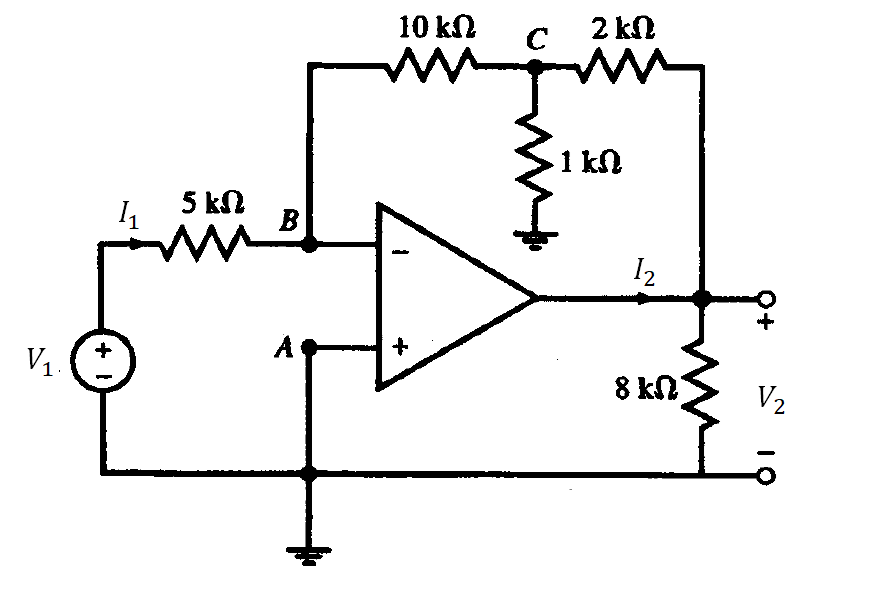
Solución del a). Se aplica la LKC a cada nodo para obtener la ecuación correspondiente. En el nodo A, se tiene que

$\displaystyle V_A = 0$

En el nodo B,

$\displaystyle \sum_{j=1}^{n}{I_j} = 0$

$\displaystyle \frac{V_B - V_1}{5 \ \text{k}} + \frac{V_B - V_C}{10 \ \text{k}} = 0$

como los voltajes de los nodos A y B son nulos, entonces

$\displaystyle \frac{0 - V_1}{5 \ \text{k}} + \frac{0 - V_C}{10 \ \text{k}} = 0$

$\displaystyle - \frac{V_1}{5 \ \text{k}} - \frac{V_C}{10 \ \text{k}} = 0$

$\displaystyle - 2V_1 - V_C = 0$

Y en el nodo C,

$\displaystyle \sum_{j=1}^{n}{I_j} = 0$

$\displaystyle \frac{V_C - V_B}{10 \ \text{k}} + \frac{V_C}{1 \ \text{k}} + \frac{V_C - V_2}{2 \ \text{k}} = 0$

$\displaystyle \frac{V_C - 0}{10 \ \text{k}} + \frac{V_C}{1 \ \text{k}} + \frac{V_C - V_2}{2 \ \text{k}} = 0$

$\displaystyle \frac{V_C}{10 \ \text{k}} + \frac{V_C}{1 \ \text{k}} + \frac{V_C - V_2}{2 \ \text{k}} = 0$

$\displaystyle \frac{V_C}{10 \ \text{k}} + \frac{V_C}{1 \ \text{k}} + \frac{V_C}{2 \ \text{k}} - \frac{V_2}{2 \ \text{k}} = 0$

$\displaystyle \left(\frac{1}{10 \ \text{k}} + \frac{1}{1 \ \text{k}} + \frac{1}{2 \ \text{k}} \right) V_C - \frac{V_2}{2 \ \text{k}} = 0$

$\displaystyle \left(\frac{16}{10 \ \text{k}} \right) V_C - \frac{V_2}{2 \ \text{k}} = 0$

$\displaystyle 16 V_C - 5 V_2 = 0$

Teniendo las ecuaciones obtenidas en cada nodo

De la ecuación (2), se despeja $v_C$ .

$\displaystyle V_C = -2 V_1$

Sustituyendo este despeje en la ecuación (3), resulta

$\displaystyle 16 V_C - 5 V_2 = 0$

$\displaystyle 16 (-2 V_1) - 5 V_2 = 0$

$\displaystyle -32 V_1 - 5 V_2 = 0$

Obteniendo la relación $V_2/V_1$

$\displaystyle - 5 V_2 = 32 V_1$

$\displaystyle \frac{V_2}{V_1} = \frac{32}{-5}$

$\displaystyle \therefore \frac{V_2}{V_1} = -6.4$

Solución del b). Por ley de Ohm, se tiene que

$\displaystyle i_1 = \frac{V_1 - V_B}{5 \ \text{k}}$

Como las entradas del amplificador son cero, $V_B = 0$ . Así que

$\displaystyle I_1 = \frac{V_1 - 0}{5 \ \text{k}} = \frac{V_1}{5 \ \text{k}}$

$\displaystyle 5 \ \text{k} = \frac{V_1}{I_1}$

$\displaystyle \therefore \text{Resistencia interna} = \frac{V_1}{I_1} = 5 \ \text{k} \Omega$

Solución c). Del procedimiento del b) y $V_1 = 0.5 \ \text{V}$ y $V_B = 0$ , resulta

$\displaystyle I_1 = \frac{V_1 - V_B}{5 \ \text{k}}$

$\displaystyle I_1 = \frac{0.5 - 0}{5 \ \text{k}} = \frac{0.5}{5 \times 10^3} = 0.1 \times 10^{-3}$

Por tanto,

$\displaystyle \therefore I_1 = 0.1 \ \text{mA}$

Es necesario utilizar LKC para obtener $I_2$

$\displaystyle \sum_{j=1}^{n}{I_j} = 0$

$\displaystyle \frac{V_2}{8 \ \text{k}} - I_2 + \frac{V_2 - V_C}{2 \ \text{k}} = 0$

$\displaystyle \frac{V_2}{8 \ \text{k}} - I_2 + \frac{V_2}{2 \ \text{k}} - \frac{V_C}{2 \ \text{k}} = 0$

$\displaystyle \left(\frac{1}{8 \ \text{k}} + \frac{1}{2 \ \text{k}} \right) V_2 - \frac{V_C}{2 \ \text{k}} - I_2 = 0$

$\displaystyle \left(\frac{5}{8 \ \text{k}} \right) V_2 - \frac{V_C}{2 \ \text{k}} - I_2 = 0$

$\displaystyle I_2 = \left(\frac{5}{8 \ \text{k}} \right) V_2 - \frac{V_C}{2 \ \text{k}}$

Del resultado del a),

$\displaystyle \frac{V_2}{V_1} = -6.4$

despejando $V_2$ y sabiendo que $V_1 = 0.5$ ,

$\displaystyle V_2 = -6.4 v_1$

$\displaystyle V_2 = -6.4 (0.5)$

$\displaystyle V_2 = -3.2 \ \text{V}$

y también,

$\displaystyle V_C = -2 v_1$

$\displaystyle V_C = -2 (0.5)$

$\displaystyle V_C = - 1 \ \text{V}$

sustituyendo en la ecuación de $I_2$

$\displaystyle I_2 = \left(\frac{5}{8 \ \text{k}} \right) V_2 - \frac{V_C}{2 \ \text{k}}$

$\displaystyle I_2 = \left(\frac{5}{8 \ \text{k}} \right) (-3.2) - \frac{(-1)}{2 \ \text{k}}$

$\displaystyle I_2 = - \left(\frac{16}{8 \ \text{k}} \right) (-3.2) + \frac{1}{2 \ \text{k}}$

$\displaystyle I_2 = - \left(\frac{16}{8 \times 10^3} \right) + \frac{1}{2 \times 10^3}$

$\displaystyle I_2 = - 2 \times 10^{-3} + \frac{1}{2} \times 10^{-3} = - 1.5 \times 10^{-3}$

Por tanto,

$\displaystyle \therefore I_2 = - 1.5 \ \text{mA}$

La potencia suministrada por $V_1$ es

$\displaystyle P_1 = V_1 I_1$

$\displaystyle P_1 = (0.5)(0.1 \text{m}) = (0.5)(0.1 \ \times{-3}) = 0.05 \times 10^{-3} = 50 \times 10^{-6}$

$\displaystyle \therefore P_1 = 50 \ \mu \text{W}$

Para obtener la potencia disipada es necesario calcular primero la potencia en cada resistor. En la siguiente tabla se muestra los cálculos y resultados de la potencia potencia en cada resistor.

\displaystyle P_{1 \text{k} \Omega} = \frac{v_C^2}{1 \ \text{k}}

Sumando las potencias de cada resistor, se obtiene la potencia total disipada.

$\displaystyle P_2 = P_{1 \text{k} \Omega} + P_{2 \text{k} \Omega} + P_{5 \text{k} \Omega} + P_{8 \text{k} \Omega} + P_{10 \text{k} \Omega}$

$\displaystyle P_2 = 1 \ \text{mW} + 2.42 \ \text{mW} + 0.05 \ \text{mW} + 1.28 \ \text{mW} + 0.1 \ \text{mW}$

$\displaystyle \therefore P_2 = 4.85 \ \text{mW}$

Resistor de $1 \ \text{k} \Omega$	$\displaystyle P_{1 \text{k} \Omega} = \frac{v_C^2}{1 \ \text{k}}$ $\displaystyle P_{1 \text{k} \Omega} = \frac{(-1)^2}{1 \times 10^3} = 1 \times 10^{-3}$ $\displaystyle P_{1 \text{k} \Omega} = 1 \ \text{mW}$
Resistor de $2 \ \text{k} \Omega$	$\displaystyle P_{2 \text{k} \Omega} = \frac{(v_2 - v_C)^2}{2 \ \text{k}}$ $\displaystyle P_{2 \text{k} \Omega} = \frac{[-3.2 - (- 1)]^2}{2 \times 10^3} = 2.42 \times 10^{-3}$ $\displaystyle P_{2 \text{k} \Omega} = 2.42 \ \text{mW}$
Resistor de $5 \ \text{k} \Omega$	$\displaystyle P_{5 \text{k} \Omega} = \frac{v_1^2}{5 \ \text{k}}$ $\displaystyle P_{5 \text{k} \Omega} = \frac{(0.5)^2}{5 \times 10^3} = 0.05 \times 10^{-3}$ $\displaystyle P_{5 \text{k} \Omega} = 0.05 \ \text{mW}$
Resistor de $8 \ \text{k} \Omega$	$\displaystyle P_{8 \text{k} \Omega} = \frac{v_2^2}{8 \ \text{k}}$ $\displaystyle P_{8 \text{k} \Omega} = \frac{(-3.2)^2}{8 \times 10^3} = 1.28 \times 10^{-3}$ $\displaystyle P_{8 \text{k} \Omega} = 1.28 \ \text{mW}$
Resistor de $10 \ \text{k} \Omega$	$\displaystyle P_{10 \text{k} \Omega} = \frac{v_C^2}{10 \ \text{k}}$ $\displaystyle P_{10 \text{k} \Omega} = \frac{(-1)^2}{10 \times 10^3} = 0.1 \times 10^{-3}$ $\displaystyle P_{10 \text{k} \Omega} = 0.1 \ \text{mW}$

Análisis de circuitos con amplificadores operacionales. Circuitos eléctricos.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

$\displaystyle V_A = 0$	(1)
$\displaystyle - 2V_1 - V_C = 0$	(2)
$\displaystyle 16 V_C - 5 V_2 = 0$	(3)

Análisis de circuitos con amplificadores operacionales. Circuitos eléctricos.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta