Circuito inversor. Amplificador operacional. Circuitos eléctricos.

Introducción

En un circuito inversor la señal de entrada se conecta a través de una resistencia $R_1$ a la terminal inversora del amplificador operacional y el voltaje de la terminal de salida realimenta a la terminal inversora a través de una resistencia $R_2$ . La terminal no inversora del amplificador operacional se conecta a tierra (figura 1).

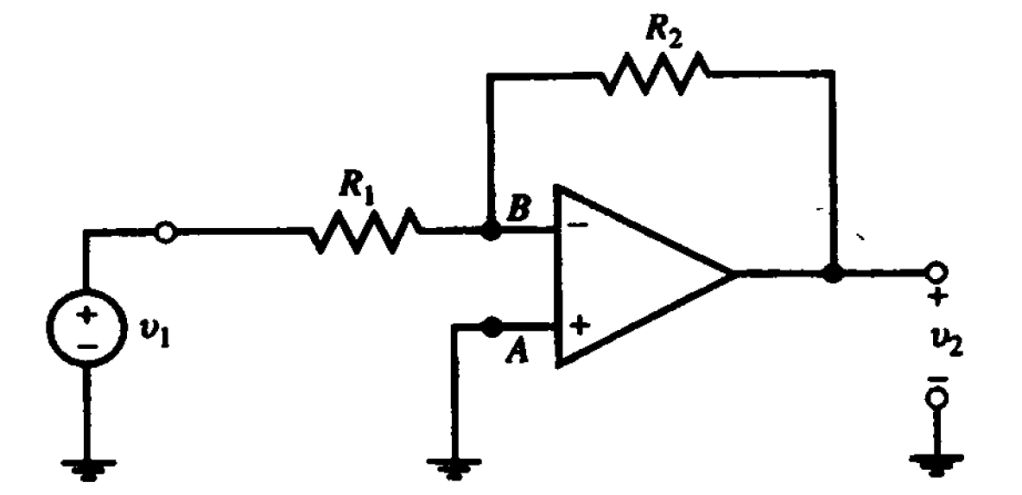
Para calcular la ganancia $v_2/v_1$ basta con obtenerlo por medio de la LKC. Entonces

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{v_B - v_1}{R_1} + \frac{v_B - v_2}{R_2} = 0$

Al no haber voltaje en $v_B=0$ ,

$\displaystyle \frac{0 - v_1}{R_1} + \frac{0 - v_2}{R_2} = 0$

$\displaystyle - \frac{v_1}{R_1} - \frac{v_2}{R_2} = 0$

$\displaystyle - \frac{v_2}{R_2} = \frac{v_1}{R_1}$

$\displaystyle \frac{v_2}{v_1} = - \frac{R_2}{R_1}$

La ganancia es negativa y está determinada por la elección de las resistencias; además, la resistencia de entrada al circuito es $R_1$ .

Problema resuelto

Problema 1. En el circuito de la figura 2 se tiene una fuente $v_s = \sin{100t}$ . Calcular $v_1$ y $v_2$ .

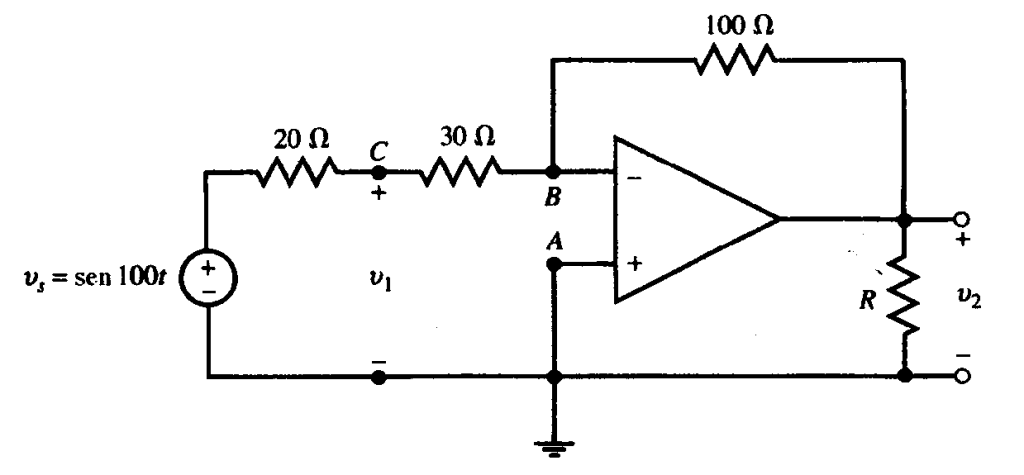
Solución. Se observa que en los nodos A y B no hay voltaje, por lo que $v_A = 0$ y $v_B = 0$ . Para obtener el valor de $v_1$ , se utiliza la división de voltaje.

$\displaystyle v_1 = \left( \frac{30}{30 + 20} \right) v_s$

$\displaystyle v_1 = \left( \frac{30}{50} \right) (\sin{100t})$

$\displaystyle \therefore v_1 = 0.6 \sin{100t}$

Luego, por LKC se tiene lo siguiente

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{v_B - v_s}{20 + 30} + \frac{v_B - v_2}{100} = 0$

$\displaystyle \frac{0 - \sin{100t}}{50} + \frac{0 - v_2}{100} = 0$

$\displaystyle - \frac{\sin{100t}}{50} - \frac{v_2}{100} = 0$

Despejando $v_2$

$\displaystyle - \frac{v_2}{100} = \frac{\sin{100t}}{50}$

$\displaystyle v_2= - \frac{100 \sin{100t}}{50}$

$\displaystyle \therefore v_2= - 2 \sin{100t} \ \text{V}$

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.