Amplificadores sustractor y diferenciador. Circuitos eléctricos.

Introducción

Una fuente de señal $v_f$ sin conexión a tierra se llama fuente flotante. Estas señales pueden amplificarse por el circuito de la figura 1.

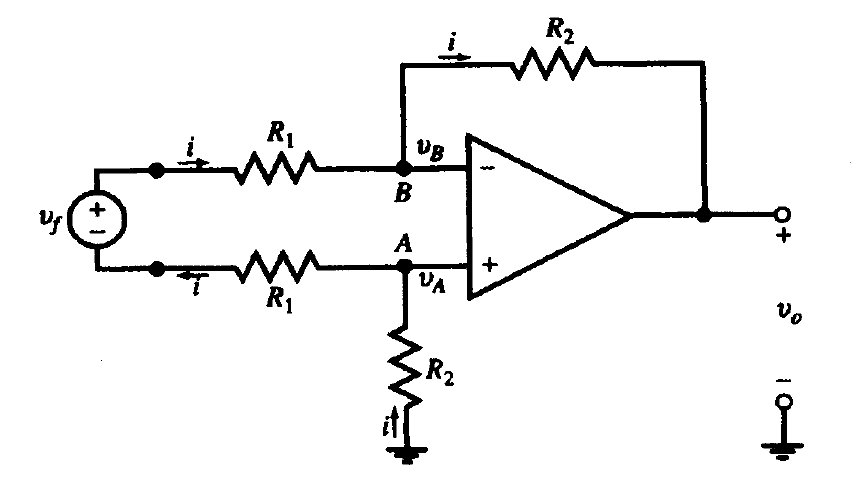
Figura 1. Amplificador operacional conextado a una fuente flotante.

Aquí las dos terminales de entrada A y B del amplificador operacional tienen el mismo voltaje. Además, por LKV a lo largo del lazo de entrada, se tiene que

$\displaystyle \sum_{j=1}^{n}{v_j} = 0$

$\displaystyle v_f = 2R_1 i$

de donde

$\displaystyle i = \frac{v_f}{2R_1}$

Las entradas del amplificador operacional no demandan corriente y, por tanto, la corriente $i$ fluye a través de la resistencia $R_2$ . Aplicando la LKV alrededor del lazo del amplificador operacional se tiene que:

$\displaystyle \sum_{j=1}^{n}{V_j} = 0$

$\displaystyle v_o + R_2 i + R_2 i = 0$

$\displaystyle v_o = - 2 R_2 i$

$\displaystyle v_o = - 2 R_2 \left(\frac{v_f}{2R_1} \right)$

$\displaystyle v_o = - \left(\frac{R_2}{R_1} \right) v_f$

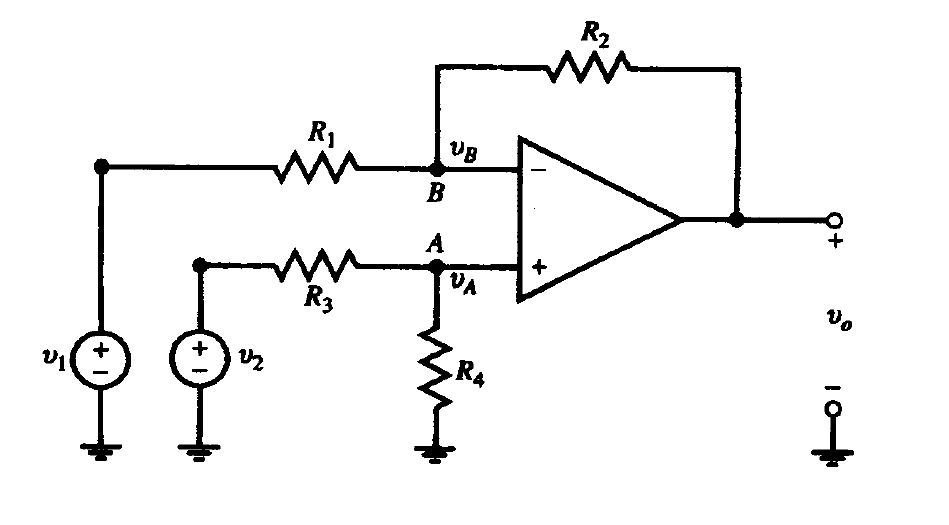
En el caso especial de que se conecten dos fuentes de voltaje $v_1$ y $v_2$ con tierra común a las entradas inversoras y no inversoras del circuito, respectivamente (figura 2), se tendría $v_f = v_1 - v_2$ y

$\displaystyle v_o = \frac{R_2}{R_1} (v_2 - v_1)$

Problema resuelto

Problema 1. Calcular $v_o$ en función de $v_1$ y $v_2$ del circuito de la figura 3.

Solución. Aplicando la LKC en el nodo A, se tiene que

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{v_A - v_2}{R_3} + \frac{v_A}{R_4} = 0$

$\displaystyle \frac{v_A}{R_3} - \frac{v_2}{R_3} + \frac{v_A}{R_4} = 0$

$\displaystyle \left(\frac{1}{R_3} + \frac{1}{R_4} \right) v_A - \frac{v_2}{R_3} = 0$

Y en el nodo B, se tiene que

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{v_B - v_1}{R_1} + \frac{v_B - v_o}{R_2} = 0$

$\displaystyle \frac{v_B}{R_1} - \frac{v_1}{R_1} + \frac{v_B}{R_2} - \frac{v_o}{R_2} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_B - \frac{v_1}{R_1} - \frac{v_o}{R_2} = 0$

Sabiendo que $v_A = v_B$ ,

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_A - \frac{v_1}{R_1} - \frac{v_o}{R_2} = 0$

Las ecuaciones son

\displaystyle \left(\frac{1}{R_3} + \frac{1}{R_4} \right) v_A - \frac{v_2}{R_3} = 0

Despejando $v_A$

\displaystyle v_A = \left(\frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} \right) \left(\frac{v_1}{R_1} + \frac{v_o}{R_2} \right) = 0

\displaystyle v_A = \left(\frac{1}{\frac{1}{R_3} + \frac{1}{R_4}} \right) \left(\frac{v_2}{R_3} \right)

Simplificando

\displaystyle v_A = \frac{R_2 v_1 + R_1 v_o}{R_1 + R_2}

Aplicando el método de igualación en las ecuaciones (3) y (4) y despejando $v_o$ , se tiene que

$\displaystyle v_A = \frac{R_4 v_2}{R_3 + R_4}$

$\displaystyle \frac{R_2 v_1 + R_1 v_o}{R_1 + R_2} = \frac{R_4 v_2}{R_3 + R_4}$

$\displaystyle R_2 v_1 + R_1 v_o = \frac{R_4 v_2(R_1 + R_2)}{R_3 + R_4}$

$\displaystyle R_1 v_o = \frac{R_4 v_2(R_1 + R_2)}{R_3 + R_4} - R_2 v_1$

$\displaystyle v_o = \frac{R_4 v_2(R_1 + R_2)}{R_1 (R_3 + R_4)} - \frac{R_2 v_1}{R_1}$

$\displaystyle \therefore v_o = \left[\frac{R_4 (R_1 + R_2)}{R_1 (R_3 + R_4)} \right] v_2 - \left(\frac{R_2}{R_1} \right) v_1$

$\displaystyle v_A = \left(\frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} \right) \left(\frac{v_1}{R_1} + \frac{v_o}{R_2} \right) = 0$	(3)
$\displaystyle v_A = \left(\frac{1}{\frac{1}{R_3} + \frac{1}{R_4}} \right) \left(\frac{v_2}{R_3} \right)$	(4)

$\displaystyle v_A = \frac{R_2 v_1 + R_1 v_o}{R_1 + R_2}$	(3)
$\displaystyle v_A = \frac{R_4 v_2}{R_3 + R_4}$	(4)

Amplificadores sustractor y diferenciador. Circuitos eléctricos.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_A - \frac{v_1}{R_1} - \frac{v_o}{R_2} = 0$	(1)
$\displaystyle \left(\frac{1}{R_3} + \frac{1}{R_4} \right) v_A - \frac{v_2}{R_3} = 0$	(2)

Amplificadores sustractor y diferenciador. Circuitos eléctricos.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta