Computadores analógicos. Circuitos eléctricos.

Introducción

Los amplificadores inversores, los circuitos sumadores y los integradores se usan para construir los bloques que configuran los computadores analógicos, utilizados para resolver ecuaciones diferenciales lineales. Se elude el uso de los derivadores a causa del considerable efecto de ruido a pesar de su bajo nivel.

Para diseñar un circuito computador, en primer lugar hay que reordenar la ecuación diferencial correspondiente, de tal forma que el término que tenga la derivada mayor esté en el primer miembro de la ecuación (lado izquierdo) y los otros en el segundo (lado derecho). Se añaden integradores y amplificadores en cascada y anidados en lazos.

Se tomará en cuenta la notación $\displaystyle x' = x'(t) = \frac{dx}{dt}$ , $\displaystyle x'' = x''(t) = \frac{d^2x}{{dt}^2}$ , y así sucesivamente.

Problema resuelto

Problema 1. Diseñar un circuito con entrada $x(t)$ que proporcione una salida $y(t)$ tal que se satisfaga la siguiente ecuación:

$\displaystyle y''(t) + 2 y'(t) + 3 y(t) = x(t)$

Solución.

Paso 1. Se reordena la ecuación diferencial de la siguiente manera

$\displaystyle y''(t) + 2 y'(t) + 3 y(t) = x(t)$

$\displaystyle y'' + 2 y' + 3 y = x$

$\displaystyle y'' = x - 2 y' - 3 y$

Paso 2. Se tomará un amplificador operacional circuito sumador de integrales (que en este caso serán de tres entradas). Recordando la fórmula y su circuito (figura 1)

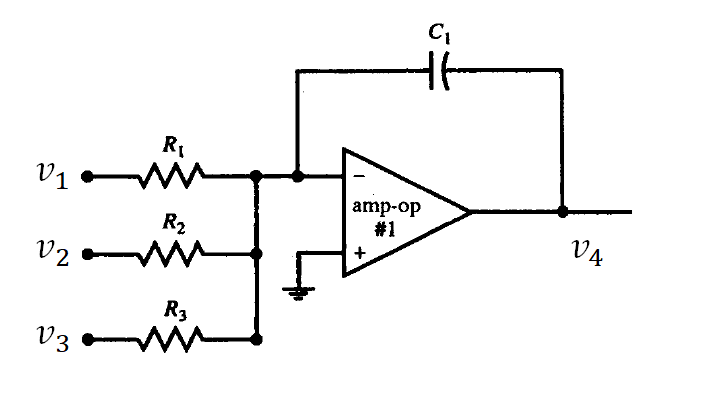
$\displaystyle v_4 = - \int{\left(\frac{v_1}{R_1 C_1} + \frac{v_2}{R_2 C_1} + \frac{v_3}{R_3 C_1} \right) \ dt}$

Figura 1. Diseño del primer amplificador operacional.

Para el caso de la expresión de la ecuación diferencial, se va integrando una vez con respecto a $t$

$\displaystyle \int{y'' \ dt} = \int{(x - 2 y' - 3 y) \ dt}$

$\displaystyle - \int{y'' \ dt} = - \int{(x - 2 y' - 3 y) \ dt}$

$\displaystyle - y' = - \int{(x - 2 y' - 3 y) \ dt}$

Comparando con la ecuación de $v_4$ , se observa que

\displaystyle v_4 = - \int{\left(\frac{v_1}{R_1 C_1} + \frac{v_2}{R_2 C_1} + \frac{v_3}{R_3 C_1} \right) \ dt}

\displaystyle - y' = - \int{(x - 2 y' - 3 y) \ dt}

donde

Si se escoge $C_1 = 1 \ \mu \text{F}$ ,

\displaystyle \frac{1}{R_1 (1 \ \mu \text{F})} = 1

\displaystyle \frac{1}{R_2 (1 \ \mu \text{F})} = 2

Con esto, la primera parte del diseño sería como el de la figura 2.

Figura 2. Resultado de la primera parte del diseño.

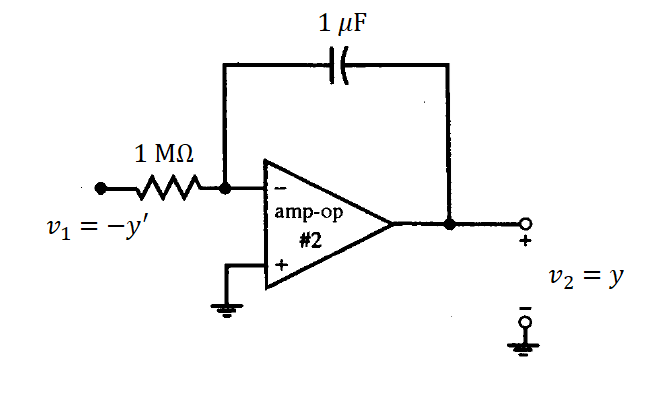
Paso 3. Ahora se diseñará un segundo amplificador operacional tipo circuito integrador. Recordando su fórmula y su circuito (figura 3)

$\displaystyle v_5 = - \frac{1}{R_4 C_2} \int{v_4 \ dt}$

Figura 3. Diseño del segundo amplificador operacional.

De la expresión $v_1 = - y'$ , se integra una vez con respecto a $t$ .

$\displaystyle v_1 = - y'$

$\displaystyle \int{v_1 \ dt} = \int{(- y') \ dt}$

$\displaystyle \int{v_1 \ dt} = - \int{y' \ dt}$

$\displaystyle v_2 = - y$

Comparando con la ecuación de $v_5$ , se observa que

\displaystyle v_5 = - \frac{1}{R_4 C_2} \int{v_4 \ dt}

\displaystyle \int{v_2 \ dt} = - \int{y' \ dt}

donde

Si se escoge $C_2 = 1 \ \mu \text{F}$ ,

\displaystyle \frac{1}{R_4 (1 \ \mu \text{F})} = 1

Con esto, la segunda parte del diseño sería como el de la figura 4.

Figura 4. Resultado de la segunda parte del diseño.

Uniendo las primeras dos partes diseñadas, se tiene lo siguiente en la figura 5.

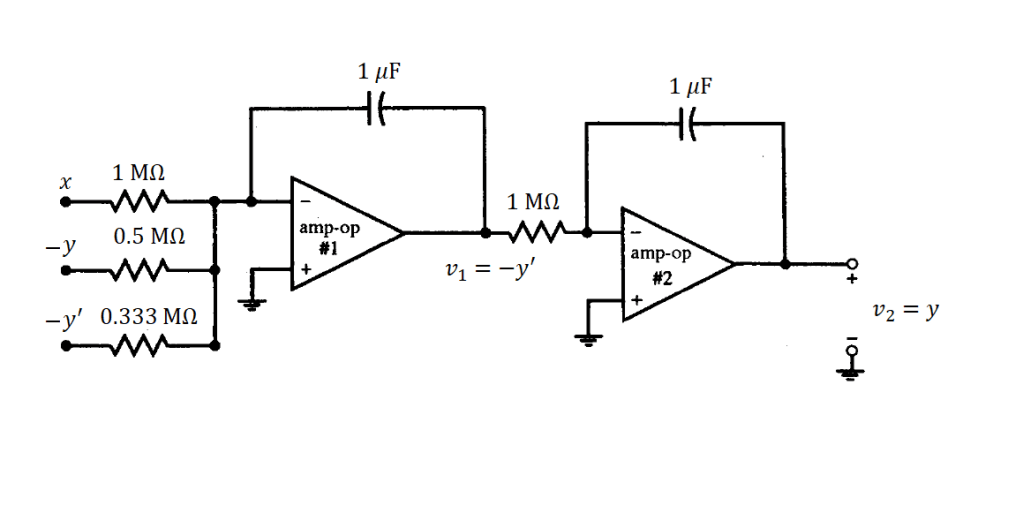
Figura 5. Conexión de la salida del primer amplificador con la entrada del segundo.

Paso 4. ¿Cómo obtener las entradas? Para ello se conecta la salida del primer amplificador con su respectiva entrada (figura 6)

*Figura 6. Conexión de la última entrada.*

Para conectar la entrada del primer amplificador con la salida del segundo es necesario que la salida sea negativa, es decir, sea $-y$ . Una solución sería diseñar un tercer amplificador operacional de tipo circuito inversor. Recordando la fórmula y su circuito (figura 7).

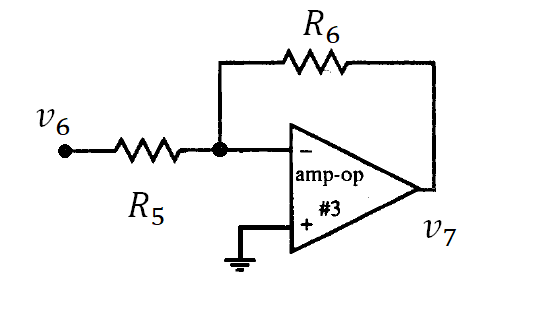
$\displaystyle v_7 = - \left( \frac{R_6}{R_5}\right) v_6$

Para que la ganancia sea unitaria, es necesario que ambos resistores tengan el mismo valor. Así, si el voltaje de entrada tiene una magnitud o valor y signo, su salida tendrá la misma magnitud o valor pero con signo opuesto. Por recomendación, se tomarán dos resistencias de 10 kΩ; con esto su salida sería

$\displaystyle v_3 = - \left( \frac{10 \ \text{k}}{10 \ \text{k}} \right) v_2$

$\displaystyle v_3 = - v_2$

Recordando que $v_2 = y$ ,

$\displaystyle v_3 = - y$

Con esto la última parte del circuito se muestra en la figura 8.

Conectando la salida del segundo amplificador con la entrada del tercero, el avance se muestra en la figura 9.

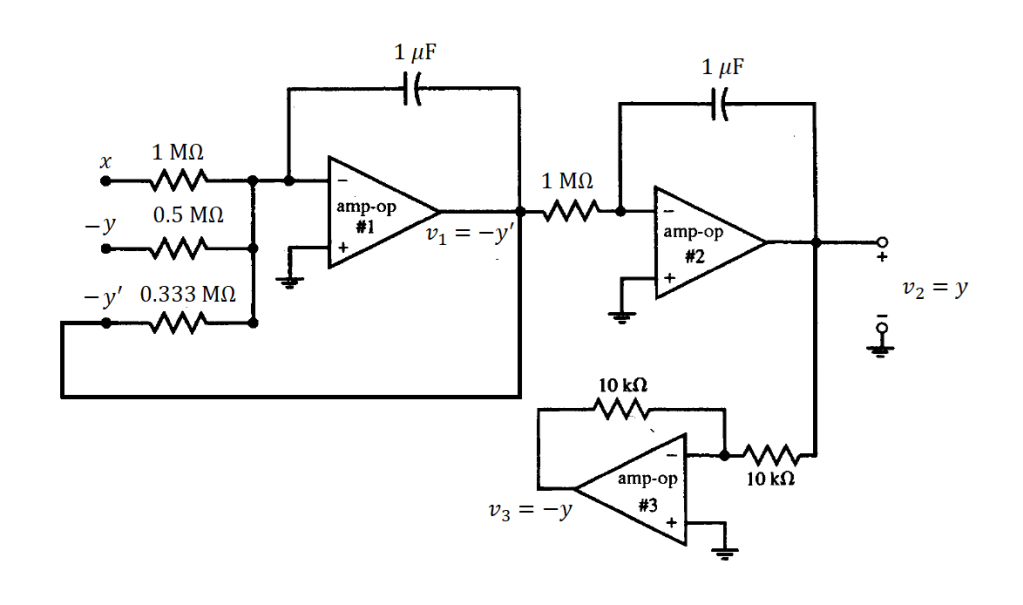
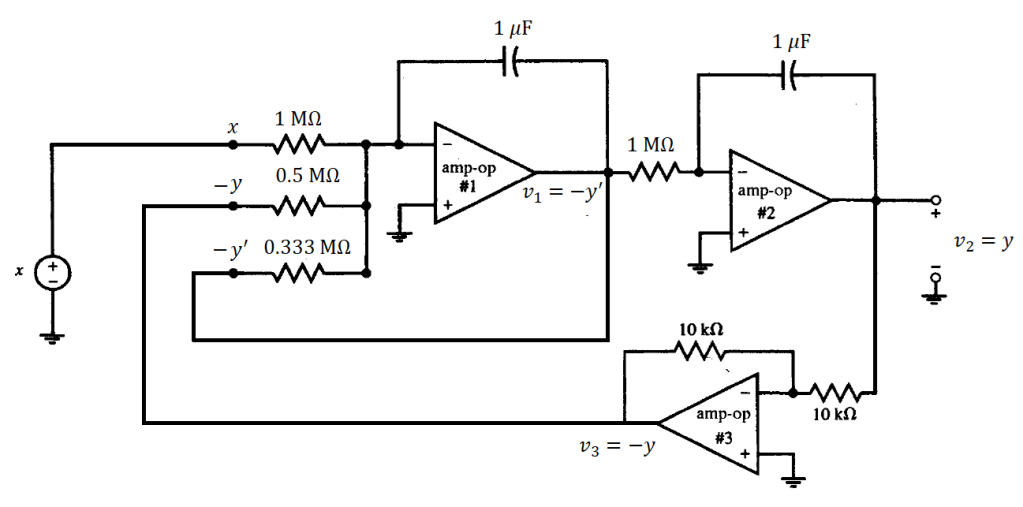
Figura 9. Conexión de la salida del amplificador #2 con la entrada del amplificador #3.

Conectando la salida del tercer amplificador con la segunda entrada del primer amplificador, se muestra en la figura 10.

Figura 10. Conexión de la salida del amplificador #3 con la segunda entrada del amplificador #1.

Finalmente, la primera entrada del primer amplificador se le añade una fuente de voltaje. El resultado final se muestra en la figura 11.

$\displaystyle \frac{1}{R_1 (1 \ \mu \text{F})} = 1$	$\displaystyle \frac{1}{R_2 (1 \ \mu \text{F})} = 2$	$\displaystyle \frac{1}{R_3 (1 \ \mu \text{F})} = 3$
$\displaystyle R_1 = 1 \ \text{M} \Omega$	$\displaystyle R_1 = 0.5 \ \text{M} \Omega$	$\displaystyle R_1 = 0.333 \ \text{M} \Omega$

Computadores analógicos. Circuitos eléctricos.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Computadores analógicos. Circuitos eléctricos.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta