Aplicaciones de espejos esféricos cóncavos
Como los espejos esféricos cóncavos concentra los rayos luminosos se utilizan en linternas de mano, en reflectores, faros de automóvil, dentistas que los introducen en la boca a sus pacientes. También en los telescopios reflectores para reflejar los rayos luminosos y concentrarlos en un punto, y con la ayuda de un espejo secundario, desviarlos para que la imagen real se forme fuera. Con estos últimos instrumentos ha sido posible descubrir estrellas, galaxias y nebulosas muy distantes.

Una aplicación a nivel industrial es concentrar los rayos de luz sobre su foco, en el cual se coloca un recipiente que concentra todos los rayos solares y que como alcanza temperaturas muy altas, funde diversas sustancias, como metales. Otro uso es hacer pasar por este punto un líquido como agua que circula por el interior de un tubo ennegrecido. El agua se calienta a muy altas temperaturas y desprende vapor, que al ser acoplado a un generador produce electricidad.
También en los hogares puede usarse para calentar agua. Los espejos esféricos cóncavos también se usan para percibir detalles en la cara, como en peluquerías y centros de maquillaje, gracias a que amplían mucho la imagen.
Distancia entre la imagen y el espejo esférico
La ecuación que calcula la distancia entre la imagen y el espejo esférico cóncavo es
Donde:
es la distancia del objeto al espejo, en metros (m).
es la distancia de la imagen al espejo, en metros (m).
es la distancia focal, en metros (m).
Aumento de la imagen
El tamaño de la imagen de un objeto puede ser mayor o menor, ello dependerá de la posición donde sea colocado. A la relación del tamaño de la imagen y el tamaño del objeto se le denomina aumento o ampliación.
Un número inferior a 1 indica que la imagen formada es menor que la del objeto y, por tanto, se presenta una reducción. Por el contrario, si el número es mayor a 1, se da un incremento en el tamaño de la imagen. Un aumento igual a 2 significa que la imagen es dos veces mayor que el objeto, y si es igual a 0.25 (1/4) indica que la imagen es cuatro veces más pequeña que el objeto.
La ecuación para calcular el aumento de la imagen se aplica a espejos cóncavos y convexos, lentes convergentes y divergentes. Junto con otros parámetros, se utiliza para fabricarlos con características tales que permitan reflejar la imagen a cierta distancia, aumentarla o disminuirla en cierta proporción; por ejemplo, que se forme antes o delante de la retina del ojo.
| Donde: | Donde : |
Problemas resueltos
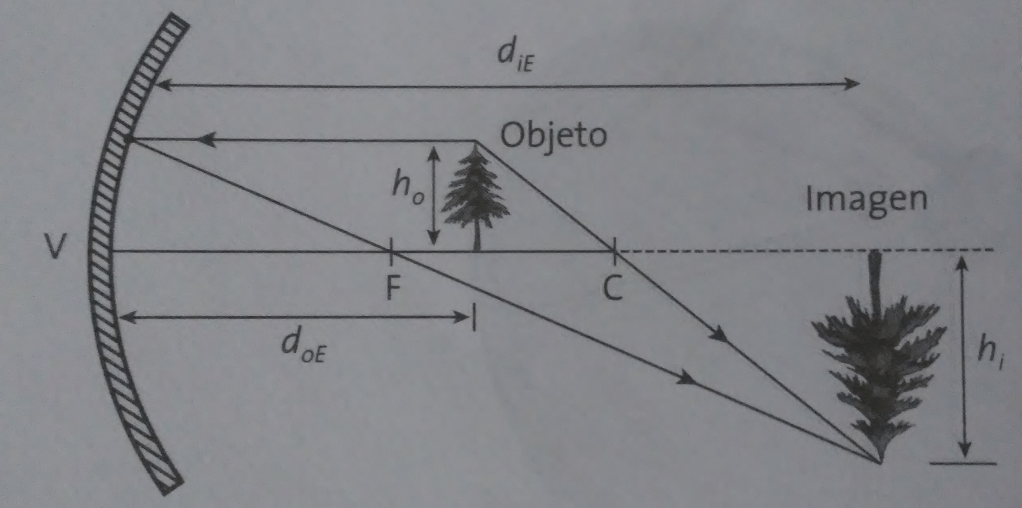
Problema 1. Un objeto de 4 (cm) de altura se coloca a 15 (cm) de un espejo esférico cóncavo. Si la imagen formada se localiza a 22.5 (cm) de éste, ¿qué altura tiene?
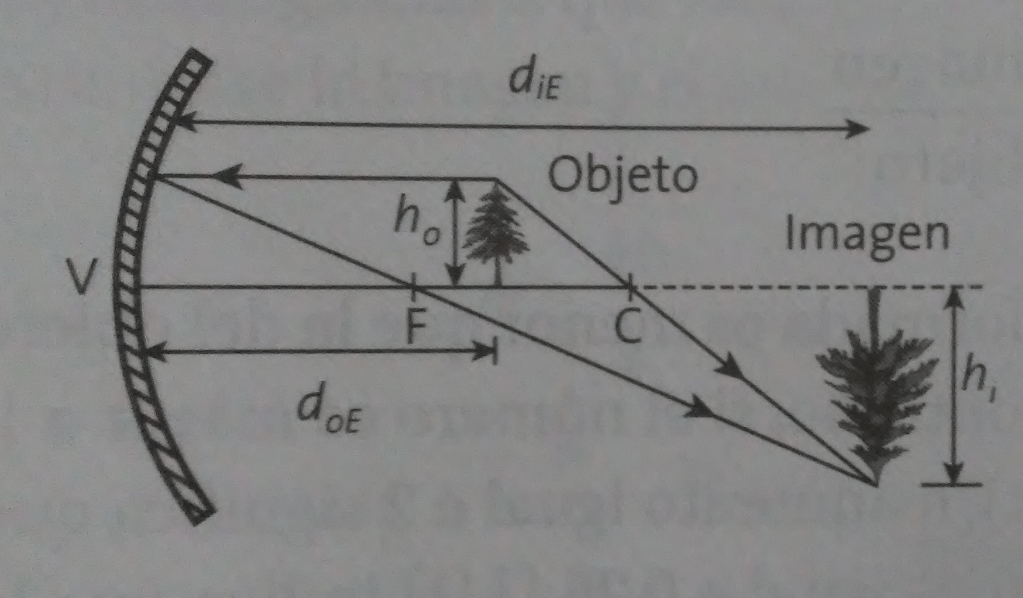
Solución. Primero se determina el aumento de la imagen utilizando la fórmula (donde toma en cuenta las distancias)
Sustituyendo
Ahora nuevamente tomando la fórmula del aumento de la imagen (donde toma en cuenta las alturas)
Se despeja
Y sustituyendo
Problema 2. Un objeto de 5 (cm) de altura se coloca a 10 (cm) e un espejo esférico cóncavo. Si éste presenta una distancia focal de 25 (cm), calcular respecto a la imagen:
- a) La distancia a la que se forma.
- b) El aumento que tiene.
- c) Su altura.
- d) Las características principales que presenta.
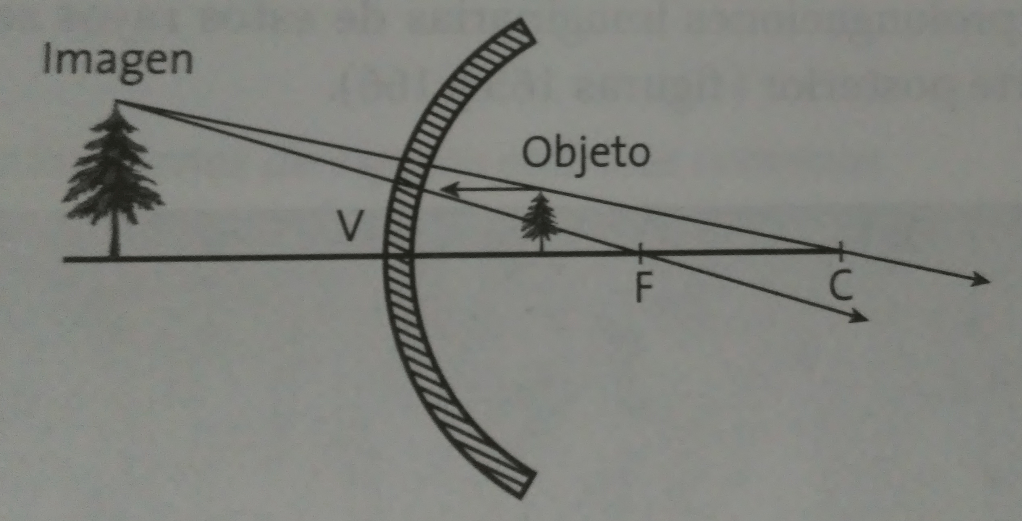
Solución del a). Tomando la fórmula
Despejando
Sustituyendo
El signo negativo indica que la imagen se forma detrás del espejo.
Solución del b). Se calcula el aumento donde toma en cuenta las distancias.
Sustituyendo
Esta fórmula no toma en cuenta el signo.
Solución del c). Se calcula la altura tomando la fórmula del aumento (donde considere las alturas).
Despejando la altura
Sustituyendo
Solución del d). Las características principales que presenta son
- El objeto está entre el vértice y el foco.
- La imagen es 1.66 veces mayor que la del objeto que la produce.
- La imagen es virtual.
- La imagen se forma detrás del espejo.
- La imagen es derecha.
- Se trata del quinto caso de espejos esféricos cóncavos.