Lentes. Física.

Introducción

Una lente es un cuerpo transparente limitado por dos caras esféricas o por una esférica y una plana. Su función es aumentar o reducir la imagen que se ve a través de ellos. Refractan los rayos luminosos que los atraviesan haciéndolos que diverjan o converjan.

Las lentes se utilizan en lupas, microscopios, anteojos, cámaras fotográficas, binoculares (prismáticos), cámaras de televisión, proyectores de cine, telescopios, etc. Son de dos tipos: convergentes o divergentes.

Elementos que forman una lente

Los elementos principales que integran una lente son: centro óptico (C), eje principal (EP), foco (F), doble distancia focal (2F) y eje secundario (ES). Su localización se muestra en la figura y su definición en la siguiente tabla. Son importantes para la construcción de todo tipo de lentes como los usados en anteojos y otros instrumentos, ya que en función del problema que presenten los ojos, el técnico sabrá que aumento se necesita, qué tipo de lente se requiere, convergente o divergente, y qué curvatura debe tener.

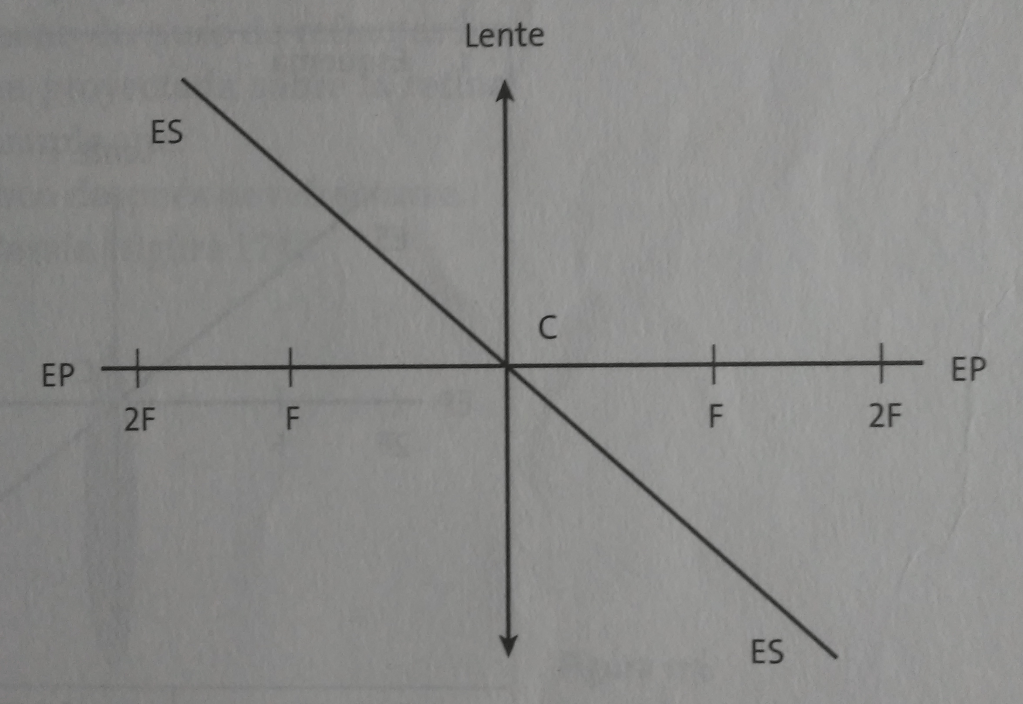
C	Centro óptico	Punto de la lente en donde el rayo de luz que pasa por él no sufre desviación.
F	Foco	Punto por donde pasan los rayos de luz refractados o sus prolongaciones. Es la distancia focal.
EP	Eje principal	Recta que pasa por el centro óptico y los focos principales de la lente.
ES	Eje secundario	Cualquier recta que pasa por el centro óptico (C).
2F	Doble distancia focal	Es el centro de curvatura de la lente.

Potencia de una lente

Al inverso de la distancia focal ( $d_F$ ) se le denomina potencia de una lente. Se define como la capacidad de una lente o espejo para hacer converger un haz de rayos paralelos. Permite conocer qué distancia focal se le debe dar a la lente, para que después de que los rayos se refracten, se enfoquen, por ejemplo, en el lugar correcto del ojo y se formen nítidamente las imágenes. Sus unidades son las dioptrías (D) y la ecuación para calcularla es

$\displaystyle P_L = \frac{1}{d_F}$

Donde

$P_L$ es la potencia de la lente, en dioptrías (D).
$d_F$ es la distancia focal, en metros (m).

Características de las imágenes de las lentes

Las reglas y ecuaciones dadas para espejos esféricos son válidas, también, para lentes, con la salvedad de que, en lugar de ser rayos reflejados, son refractados. La imagen observada en estas lentes depende de la posición del objeto, pero siempre intervienen dos rayos que proceden de un mismo punto del objeto y que al refractarse y cortarse dan la imagen correspondiente.