Introducción

En las lentes divergentes o negativas el espesor disminuye de los bordes hacia el centro, así que los extremos son más gruesos que éste. Se caracterizan por que los rayos paralelos al eje principal se separan al refractarse y dan la impresión de que producen del mismo foco principal. Hay tres tipos de estas lentes: bicóncava, plano cóncava y menisco divergente. el uso de alguna de ellas será consecuencia del tipo de imagen que se requiera lograr o problema que se deba corregir.

Menisco divergente
Bicóncava
Plano cóncava

Figura 1. Tipos de lentes divergentes.

Figura 2. Lente divergente.

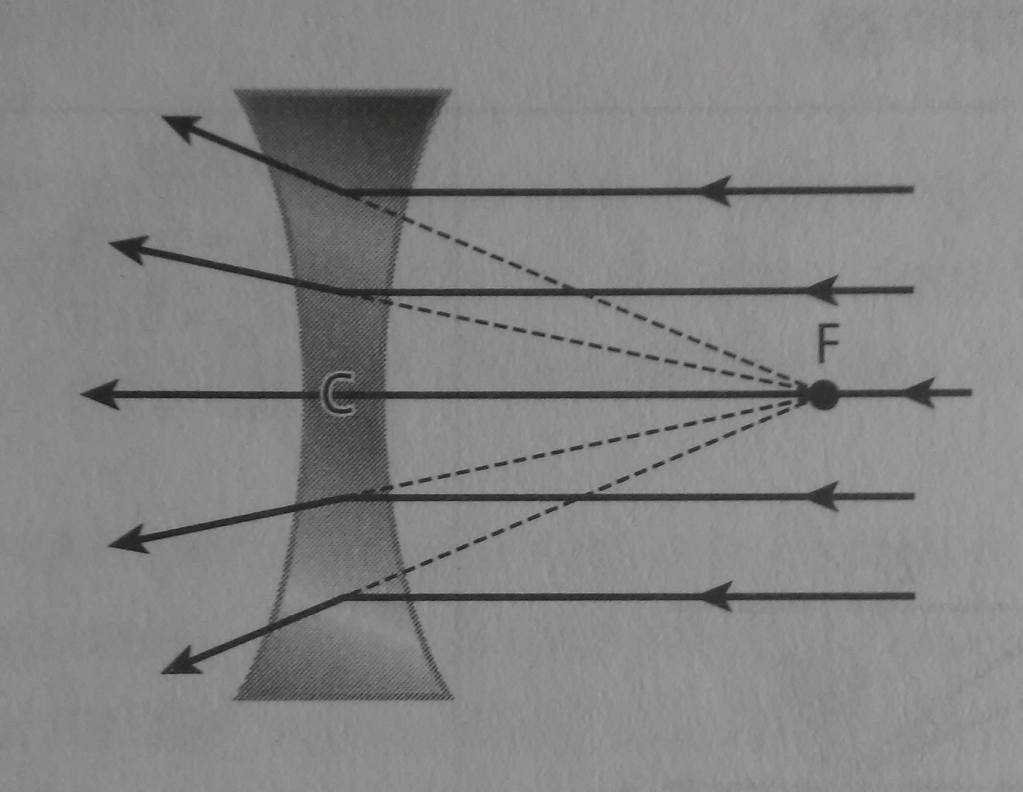
Formación de imágenes en lentes divergentes

Las lentes divergentes siempre producen imágenes virtuales y por tanto su distancia focal será negativa, de menor tamaño que la original y derechas. La ecuación que calcula la distancia de la imagen a la lente divergente es la siguiente

\displaystyle \frac{1}{d_{oL}} + \frac{1}{d_{iL}} = - \frac{1}{d_F}

Donde

  • d_{oL} es la distancia del objeto a la lente, en metros (m).
  • d_{iL} es la distancia de la imagen a la lente, en metros (m).
  • d_F es la distancia focal, en metros (m).
Figura 1. Imagen de una lente divergente.

Usos de lentes divergentes

Las lentes divergentes se montan en anteojos para corregir la miopía (visión corta). Las personas con este padecimiento enfocan los objetos cercanos, pero no los más lejanos, así que cuando no usan anteojos tienen que acercarse mucho el texto que están leyendo. El problema se debe a la excesiva curvatura del cristalino, que hace que las imágenes se formen delante de la retina. el uso de lentes divergentes tiene como función refractar los rayos, alejándolos del eje principal antes de que entren al ojo para que se enfoquen en lugar correcto.

Problema resuelto

Problema. Un objeto de 5 (cm) de altura se coloca a 18 (cm) de una lente divergente que tiene una distancia focal de 12 (cm). Calcular, respecto a la imagen:

  • a) La distancia a la que se forma.
  • b) El aumento que tiene.
  • c ) La altura.
  • d) Las características principales que presenta.

Solución. Se tiene estos datos en la siguiente figura

Figura 2.

Solución del inciso a). Tomando la ecuación de lentes divergentes

\displaystyle \frac{1}{d_{oL}} + \frac{1}{d_{iL}} = - \frac{1}{d_F}

Se despeja d_{iL}

\displaystyle \frac{1}{d_{iL}} = - \frac{1}{d_{oL}} - \frac{1}{d_F}

\displaystyle d_{iL} = \frac{1}{- \frac{1}{d_{oL}} - \frac{1}{d_F}}

Sustituyendo

\displaystyle d_{iL} = \frac{1}{- \frac{1}{18 \ (cm)} - \frac{1}{12 \ (cm)}

\displaystyle \therefore d_{iL} = -7.2 \ (cm)

Solución del inciso b). Tomando la fórmula para calcular el aumento (donde toma en cuenta las distancias)

\displaystyle A = \frac{d_{iL}}{d_{oL}}

Se sustituye (donde d_{iL} no toma en cuenta el signo sino solo el valor)

\displaystyle A = \frac{7.2 \ (cm)}{18 \ (cm)}

\displaystyle \therefore A = 0.4 \ (cm)

Esto significa que como el aumento es menor de uno, la imagen tiene un tamaño inferior al objeto.

Solución del inciso c). Tomando la ecuación del aumento (donde toma en cuenta las alturas)

\displaystyle A = \frac{h_i}{h_o}

Se despeja h_i

\displaystyle h_i = A \cdot h_o

\displaystyle h_i = (0.4)(5 \ cm)

\displaystyle \therefore h_i = 2 \ (cm)

Solución del inciso d). Se concluye que

  • En lentes divergentes el objeto siempre va a estar después de la imagen.
  • La imagen que se produce está dentro de la distancia focal y centro óptico.
  • La imagen producida es menor que el objeto en un factor de 0.4.
  • La imagen es derecha.
  • Se trata del único caso que se presenta en lentes divergentes.
Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Un comentario sobre “Lentes divergentes. Física.”

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.