Un circuito resistencia-capacitor () en serie es aquel en donde se unen una o varias resistencia (
) y uno o varios capacitores (
) a un dispositivo que les suministra corriente alterna.
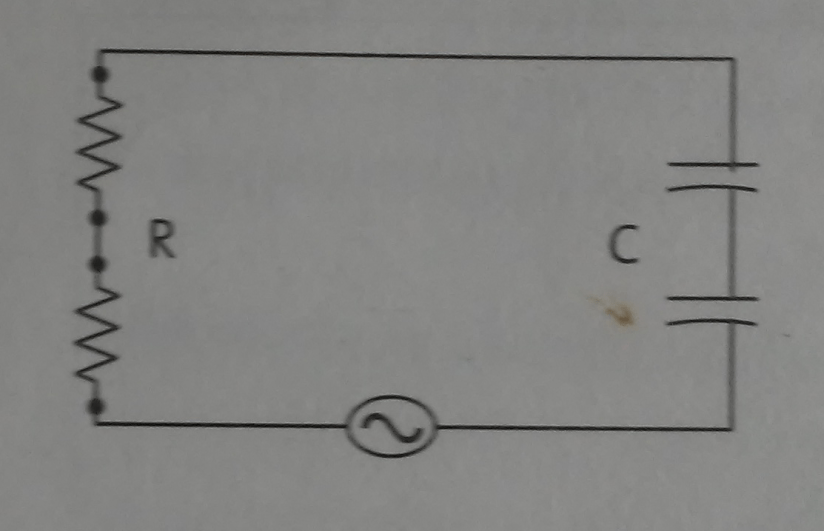
Figura 1. Esquema general de un circuito RC. 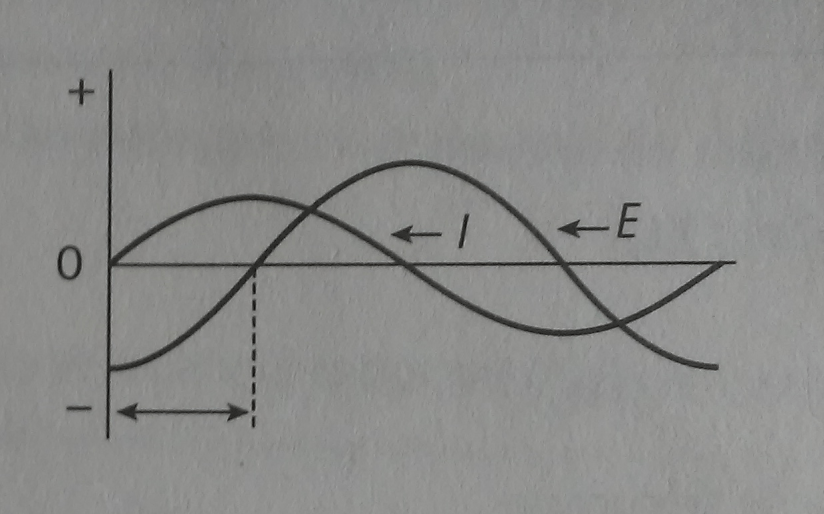
Figura 2. Desfasamiento de un circuito RC. 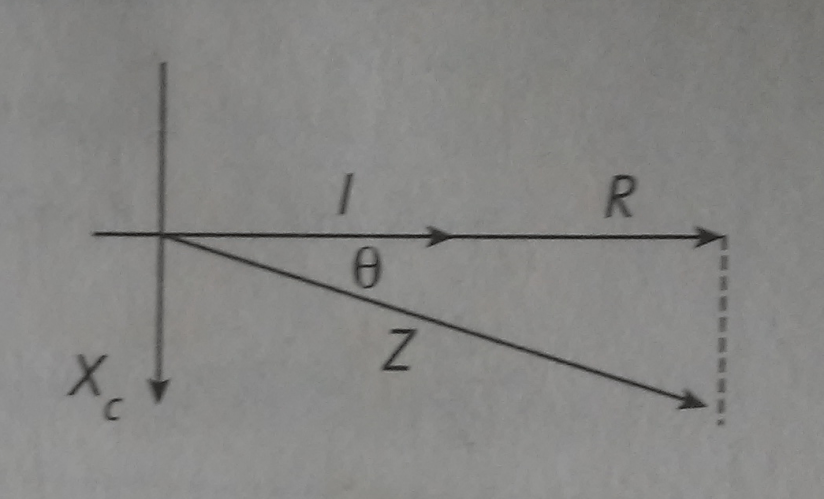
Figura 3. Relación entre variables de un circuito RC.
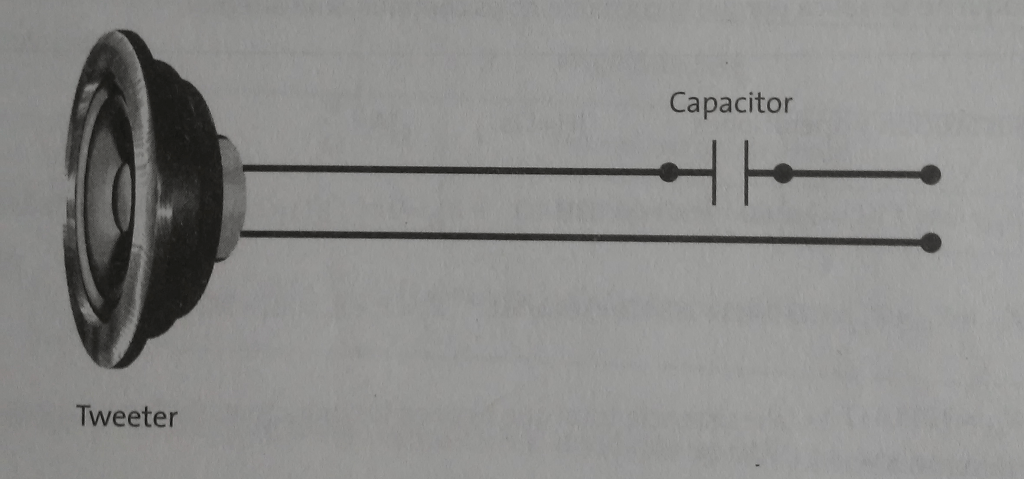
Una de las funciones del capacitor es bloquear las frecuencias bajas y dejar pasar las frecuencias altas, por eso se conecta en serie al tweeter, para que deje exclusivamente las frecuencias altas y trabaje de manera eficiente.
Los circuitos resistencia-capacitor () de corriente alterna en serie tienen como característica que el ángulo de fase es negativo, por lo que se encuentra entre -90° y 0°, lo que indica que la corriente está adelantada respecto a la tensión.
Si los motores en un sistema de acondicionamiento de aire de una sala de espectánculos muestran un retraso de fase de 30% (retraso de corriente respecto a tensión), la potencia perdida por calentamiento eléctrico aumenta aproximadamente también en esta cantidad. Este retraso de fase pueden reducir conectando capacitores. Las ecuaciones resistencia-capacitor de corriente alterna en serie son:
Donde:
es la impedancia, en Ohms (
).
es la resistencia, en Ohms (
).
es la reactancia capacitiva, en Ohms (
).
Donde:
es la intensidad de corriente perteneciente a la impedancia, en Amperes (A).
es la tensión de corriente perteneciente a la impedancia, en volts (V).
es la impendiancia, en Ohms (
).
Donde:
es la intensidad de corriente perteneciente a la resistencia, en Amperes (A).
es la tensión de corriente perteneciente a la resistencia, en volts (V).
es la resistencia, en Ohms (
).
Donde:
es la intensidad de corriente perteneciente a la reactancia capacitiva, en Amperes (A).
es la tensión de corriente perteneciente a la reactancia capacitiva, en volts (V).
es la reactancia capacitiva, en Ohms (
).
Donde:
es la tensión de corriente perteneciente a la impedancia, en volts (V).
es la tensión de corriente pertenenciente a la resistencia, en volts (V).
es la tensión de corriente pertenenciente a la reactancia capacitiva, en volts (V).
Donde:
es la reactancia capacitiva, en Ohms (
).
es la frenciencia, en Hertz (Hz).
es la capacitancia, en Farad (F).
Donde:
es el ángulo de fase, en grados (°).
es la reactancia capacitiva, en Ohms (
).
es la resistencia, en Ohms (
).
Problema resuelto
Problema. A una fuente de ca de 120 (V) y frecuencia de 60 (Hz) se unen dos resistencias de 70 y 90 () y dos capacitores de 40 y 80 (
F), todos conectados en serie. Para este circuito eléctrico, calcular:
- a) Intensidad de la corriente.
- b) Ángulo de fase.
Solución. Se determina la resistencia total
Calculando la primera reactancia capactiva
Calculando la primera reactancia capactiva
Con esto se puede obtener la reactancia capactiva total
La impedancia es
Solución del a). La corriente es
Solución del b). Por medio de la tangente
°
I’ve been absent for a while, but now I remember why I used to love this blog. Thanks , I will try and check back more often. How frequently you update your web site?
Me gustaMe gusta
Hi! This website has the latest physics topics that ended from the end of October. I’m preparing for more content dedicated to linear albegra themes starting in January.
Me gustaMe gusta
at the moment I am only correcting vector calculus content. Regards…
Me gustaMe gusta