Vector normal. Cálculo vectorial.

Introducción

Sea $C$ una curva suave en un intervalo abierto $I$ representada por $\mathbf{r}$ . Si $\mathbf{T}' (t) \ne 0$ , entonces el vector unitario normal principal en $t$ se define como

$\displaystyle \mathbf{N} (t) = \frac{\mathbf{T} ' (t)}{|| \mathbf{T} ' (t) ||}$

Problemas resueltos

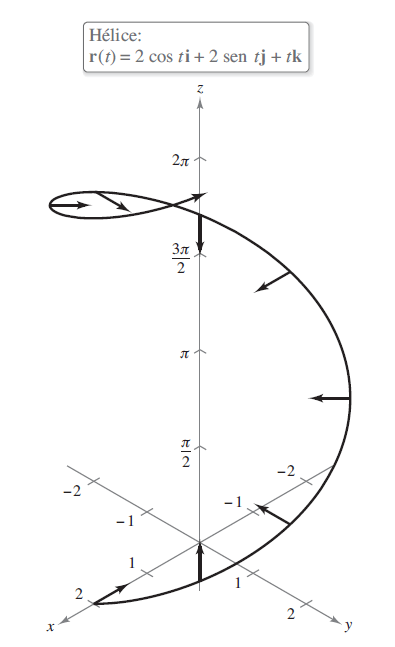
Problema 1. Encontrar $\mathbf{N} (t)$ y $\mathbf{N} (1)$ para la curva representada por $\mathbf{r} (t) = 3t \mathbf{i} + 2t^2 \mathbf{j}$ .

Solución. De la función dada por el problema, se determina su primera derivada

$\displaystyle \mathbf{r} (t) = 3t \mathbf{i} + 2t^2 \mathbf{j}$

$\displaystyle \frac{d}{dt} [\mathbf{r} (t)] = \frac{d}{dt} [3t \mathbf{i} + 2t^2 \mathbf{j}]$

$\displaystyle \mathbf{r}' (t) = \frac{d}{dt} (3t) \mathbf{i} + \frac{d}{dt} (2t^2) \mathbf{j}$

$\displaystyle \mathbf{r}' (t) = 3 \mathbf{i} + 4t \mathbf{j}$

Determinando su magnitud

$\displaystyle ||\mathbf{r}' (t)|| = ||3 \mathbf{i} + 4t \mathbf{j}||$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{{(3)}^2 + {(4t)}^2}$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{9 + 16t^2}$

Tomando la fórmula del vector unitario tangente y sustituyendo resulta lo siguiente

$\displaystyle \mathbf{T} (t) = \frac{\mathbf{r}' (t)}{|| \mathbf{r}' (t)||}$

$\displaystyle \mathbf{T} (t) = \frac{3 \mathbf{i} + 4t \mathbf{j}}{\sqrt{9 + 16t^2}}$

$\displaystyle \mathbf{T} (t) = \frac{1}{\sqrt{9 + 16t^2}} \left( 3 \mathbf{i} + 4t \mathbf{j} \right)$

De este último resultado, se determina su primera derivada

$\displaystyle \frac{d}{dt} [\mathbf{T} (t)] = \frac{d}{dt} \left[\frac{1}{\sqrt{9 + 16t^2}} \left( 3 \mathbf{i} + 4t \mathbf{j} \right) \right]$

$\displaystyle \frac{d}{dt} [\mathbf{T} (t)] = \frac{d}{dt} \left[\frac{3 \mathbf{i} + 4t \mathbf{j}}{\sqrt{9 + 16t^2}} \right]$

$\displaystyle \mathbf{T}' (t) = \frac{(\sqrt{9 + 16t^2}) \frac{d}{dt} (3 \mathbf{i} + 4t \mathbf{j}) - (3 \mathbf{i} + 4t \mathbf{j}) \frac{d}{dt} (\sqrt{9 + 16t^2})}{{(\sqrt{9 + 16t^2})}^2}$

$\displaystyle \mathbf{T}' (t) = \frac{1}{{(\sqrt{9 + 16t^2})}^2} \left[(\sqrt{9 + 16t^2}) \frac{d}{dt} (3 \mathbf{i} + 4t \mathbf{j}) - (3 \mathbf{i} + 4t \mathbf{j}) \frac{d}{dt} (\sqrt{9 + 16t^2}) \right]$

$\displaystyle \mathbf{T}' (t) = \frac{1}{{(\sqrt{9 + 16t^2})}^2} \left[(\sqrt{9 + 16t^2}) (0 \mathbf{i} + 4 \mathbf{j}) - (3 \mathbf{i} + 4t \mathbf{j}) \frac{32t}{2\sqrt{9 + 16t^2}} \right]$

$\displaystyle \mathbf{T}' (t) = \frac{1}{{(\sqrt{9 + 16t^2})}^2} \left[(\sqrt{9 + 16t^2}) (0 \mathbf{i} + 4 \mathbf{j}) \cdot \frac{\sqrt{9 + 16t^2}}{\sqrt{9 + 16t^2}} - (3 \mathbf{i} + 4t \mathbf{j}) \frac{16t}{\sqrt{9 + 16t^2}} \cdot \frac{\sqrt{9 + 16t^2}}{\sqrt{9 + 16t^2}} \right]$

$\displaystyle \mathbf{T}' (t) = \frac{1}{{(\sqrt{9 + 16t^2})}^2} \left[ \frac{(\sqrt{9 + 16t^2})^2}{\sqrt{9 + 16t^2}} \cdot (0 \mathbf{i} + 4 \mathbf{j}) - \frac{\sqrt{9 + 16t^2}}{(\sqrt{9 + 16t^2})^2} \cdot (48t \mathbf{i} + 64t^2 \mathbf{j}) \right]$

$\displaystyle \mathbf{T}' (t) = \frac{1}{{(\sqrt{9 + 16t^2})}^2} \left[ \frac{(9 + 16t^2)}{\sqrt{9 + 16t^2}} \cdot (0 \mathbf{i} + 4 \mathbf{j}) - \frac{1}{\sqrt{9 + 16t^2}} \cdot (48t \mathbf{i} + 64t^2 \mathbf{j}) \right]$

$\displaystyle \mathbf{T}' (t) = \frac{1}{{(\sqrt{9 + 16t^2})}^2} \cdot \frac{1}{{\sqrt{9 + 16t^2}}} \left[(9 + 16t^2) \cdot (0 \mathbf{i} + 4 \mathbf{j}) - (1) \cdot (48t \mathbf{i} + 64t^2 \mathbf{j}) \right]$

$\displaystyle \mathbf{T}' (t) = \frac{1}{{(\sqrt{9 + 16t^2})}^3} \left[0 \mathbf{i} + (36 + 64t^2) \mathbf{j} - 48t \mathbf{i} - 64t^2 \mathbf{j} \right]$

$\displaystyle \mathbf{T}' (t) = \frac{1}{{(\sqrt{9 + 16t^2})}^3} \left(- 48t \mathbf{i} + 36 \mathbf{j} \right)$

$\displaystyle \mathbf{T}' (t) = \frac{12}{{(\sqrt{9 + 16t^2})}^3} \left(- 4t \mathbf{i} + 3 \mathbf{j} \right) = \frac{12}{{(9 + 16t^2)}^{3/2}} \left(- 4t \mathbf{i} + 3 \mathbf{j} \right)$

Obteniendo la magnitud de este último resultado

$\displaystyle ||\mathbf{T}' (t)|| = ||\frac{12}{{(\sqrt{9 + 16t^2})}^3} \left(- 4t \mathbf{i} + 3 \mathbf{j} \right)||$

$\displaystyle ||\mathbf{T}' (t)|| = \sqrt{{\left[\frac{12}{{(\sqrt{9 + 16t^2})}^3} \right]}^2 \cdot {(- 4t)}^2 + {\left[\frac{12}{{(\sqrt{9 + 16t^2})}^3} \right]}^2 \cdot {(3)}^2}$

$\displaystyle ||\mathbf{T}' (t)|| = \sqrt{{\left[\frac{12}{{(\sqrt{9 + 16t^2})}^3} \right]}^2} \cdot \sqrt{{(- 4t)}^2 + {(3)}^2}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{12}{{(\sqrt{9 + 16t^2})}^3} \cdot \sqrt{16t^2 + 9} = \frac{12}{{(\sqrt{9 + 16t^2})}^3} \cdot \sqrt{9 + 16t^2}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{12}{{(\sqrt{9 + 16t^2})}^2}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{12}{9 + 16t^2}$

Determinando el vector unitario normal, resulta que

$\displaystyle \mathbf{N} (t) = \frac{\mathbf{T} ' (t)}{|| \mathbf{T} ' (t) ||}$

$\displaystyle \mathbf{N} (t) = \frac{\frac{12}{{(9 + 16t^2)}^{3/2}} \left(- 4t \mathbf{i} + 3 \mathbf{j} \right)}{\frac{12}{9 + 16t^2}}$

$\displaystyle \mathbf{N} (t) = \frac{\frac{12}{{(9 + 16t^2)}^{3/2}}}{\frac{12}{9 + 16t^2}} \ \left(- 4t \mathbf{i} + 3 \mathbf{j} \right)$

$\displaystyle \mathbf{N} (t) = \frac{1}{{(9 + 16t^2)}^{1/2}} \ \left(- 4t \mathbf{i} + 3 \mathbf{j} \right)$

$\displaystyle \therefore \mathbf{N} (t) = \frac{1}{\sqrt{9 + 16t^2}} \ \left(- 4t \mathbf{i} + 3 \mathbf{j} \right)$

Finalmente, el valor de $\mathbf{N} (1)$ (es decir, cuando $t=1$ ) es

$\displaystyle \mathbf{N} (1) = \frac{1}{\sqrt{9 + 16{(1)}^2}} \ \left[- 4(1) \mathbf{i} + 3 \mathbf{j} \right]$

$\displaystyle \mathbf{N} (1) = \frac{1}{\sqrt{9 + 16(1)}} \ \left(- 4 \mathbf{i} + 3 \mathbf{j} \right)$

$\displaystyle \mathbf{N} (1) = \frac{1}{\sqrt{9 + 16}} \ \left(- 4 \mathbf{i} + 3 \mathbf{j} \right)$

$\displaystyle \mathbf{N} (1) = \frac{1}{\sqrt{25}} \left(- 4 \mathbf{i} + 3 \mathbf{j} \right)$

$\displaystyle \therefore \mathbf{N} (1) = \frac{1}{5} \left(- 4 \mathbf{i} + 3 \mathbf{j} \right)$

Figura 1. Representación gráfica del problema 1.

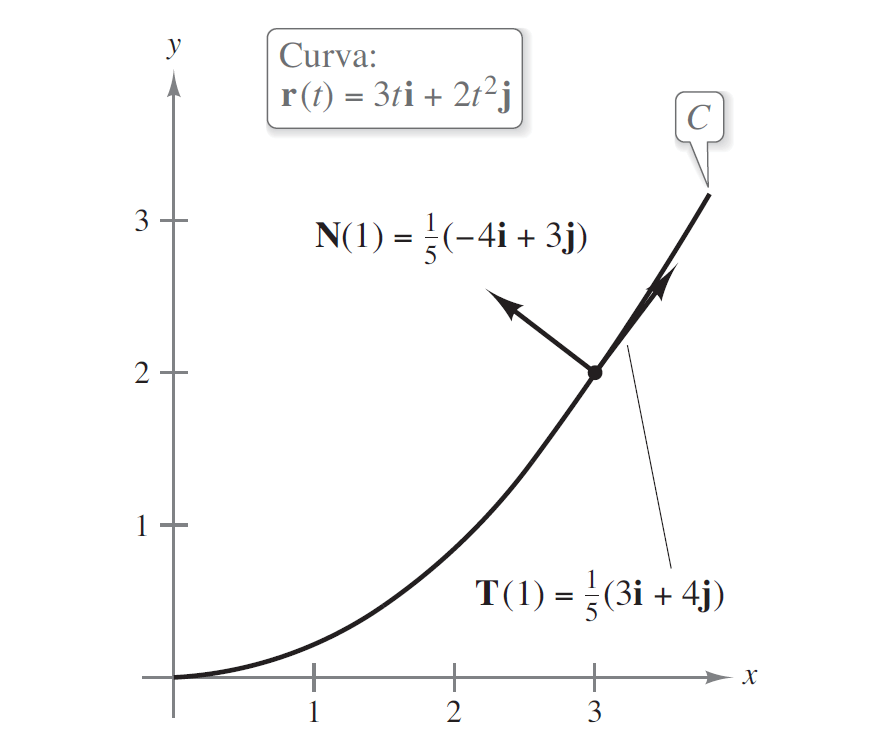
Problema 2. Encontrar el vector unitario normal principal para la hélice dada por $\displaystyle \mathbf{r} (t) = 2 \cos{t} \mathbf{i} + 2 \sin{t} \mathbf{j} + t \mathbf{k}$ .

Solución. Primero se determina la primera deriva de la función vectorial $\mathbf{r} (t)$ .

$\displaystyle \mathbf{r} (t) = 2 \cos{t} \mathbf{i} + 2 \sin{t} \mathbf{j} + t \mathbf{k}$

$\displaystyle \frac{d}{dt} [\mathbf{r} (t)] = \frac{d}{dt} [2 \cos{t}] \mathbf{i} + \frac{d}{dt} [2 \sin{t}] \mathbf{j} + \frac{d}{dt} [t] \mathbf{k}$

$\displaystyle \mathbf{r}' (t) = 2 \frac{d}{dt} [\cos{t}] \mathbf{i} + 2 \frac{d}{dt} [\sin{t}] \mathbf{j} + \frac{d}{dt} [t] \mathbf{k}$

$\displaystyle \mathbf{r}' (t) = - 2 \sin{t} \mathbf{i} + 2 \cos{t} \mathbf{j} + \mathbf{k}$

Después, se determina su magnitud

$\displaystyle ||\mathbf{r}' (t)|| = ||- 2 \sin{t} \mathbf{i} + 2 \cos{t} \mathbf{j} + \mathbf{k}||$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{{(- 2 \sin{t})}^2 + {(2 \cos{t})}^2 + {(1)}^2}$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{4 \cos^2{t} + 4 \sin^2{t} + 1}$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{4 (\sin^2{t} + \cos^2{t}) + 1}$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{4 (1) + 1} = \sqrt{4 + 1}$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{5}$

Tomando la fórmula de vector unitario tangentes y sustituyendo

$\displaystyle \mathbf{T} (t) = \frac{\mathbf{r}' (t)}{||\mathbf{r}' (t)||}$

$\displaystyle \mathbf{T} (t) = \frac{- 2 \sin{t} \mathbf{i} + 2 \cos{t} \mathbf{j} + \mathbf{k}}{\sqrt{5}}$

$\displaystyle \mathbf{T} (t) = \frac{1}{\sqrt{5}} (- 2 \sin{t} \mathbf{i} + 2 \cos{t} \mathbf{j} + \mathbf{k})$

De este último resultado se obtiene su primera derivada

$\displaystyle \frac{d}{dt} [\mathbf{T} (t)] = \frac{d}{dt} [\frac{1}{\sqrt{5}} (- 2 \sin{t} \mathbf{i} + 2 \cos{t} \mathbf{j} + \mathbf{k})]$

$\displaystyle \mathbf{T}' (t) = - \frac{2}{\sqrt{5}} \frac{d}{dt} [\sin{t}] \mathbf{i} + \frac{2}{\sqrt{5}} \frac{d}{dt} [\cos{t}] + \frac{1}{\sqrt{5}} \frac{d}{dt} [1] \mathbf{k}$

$\displaystyle \mathbf{T}' (t) = - \frac{2}{\sqrt{5}} \cos{t} \mathbf{i} - \frac{2}{\sqrt{5}} \sin{t} + \frac{1}{\sqrt{5}} (0) \mathbf{k}$

$\displaystyle \mathbf{T}' (t) = - \frac{2}{\sqrt{5}} \cos{t} \mathbf{i} - \frac{2}{\sqrt{5}} \sin{t} = \frac{2}{\sqrt{5}} (-\cos{t} \mathbf{i} - \sin{t})$

Y también su magnitud

$\displaystyle ||\mathbf{T}' (t)|| = ||- \frac{2}{\sqrt{5}} \cos{t} \mathbf{i} - \frac{2}{\sqrt{5}} \sin{t}||$

$\displaystyle ||\mathbf{T}' (t)|| = \sqrt{{\left(- \frac{2}{\sqrt{5}} \cos{t} \right)}^2 + {\left(- \frac{2}{\sqrt{5}} \sin{t} \right)}^2}$

$\displaystyle ||\mathbf{T}' (t)|| = \sqrt{\frac{4}{5} \cos^2{t} + \frac{4}{5} \sin^2{t}}$

$\displaystyle ||\mathbf{T}' (t)|| = \sqrt{\frac{4}{5} (\cos^2{t} + \sin^2{t})}$

$\displaystyle ||\mathbf{T}' (t)|| = \sqrt{\frac{4}{5} (1)} = \sqrt{\frac{4}{5}}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{2}{\sqrt{5}}$

Usando la fórmula del vector unitario normal principal y sustituyendo, resulta que

$\displaystyle \mathbf{N} (t) = \frac{\mathbf{T} ' (t)}{|| \mathbf{T} ' (t) ||}$

$\displaystyle \mathbf{N} (t) = \frac{\frac{2}{\sqrt{5}} (-\cos{t} \mathbf{i} - \sin{t})}{\frac{2}{\sqrt{5}}}$

$\displaystyle \therefore \mathbf{N} (t) = -\cos{t} \mathbf{i} - \sin{t}$

Vector normal. Cálculo vectorial.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Vector normal. Cálculo vectorial.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta