Introducción
Si una curva suave C está dada por y
y
no se corta a sí misma en el intervalo
(excepto quizá en los puntos terminales), entonces la longitud de arco de
en ese intervalo está dada por:
Problemas resueltos
Problema 1. Hallar la longitud de arco mediante las ecuaciones paramétricas:
y
para
Solución. Para poder utilizar la fórmula de la longitud de arco, primero se va derivando la ecuación paramétrica con respecto a
, se tiene lo siguiente
Se aplica el paso anterior para la ecuación paramétrica
Después, del intervalo , los límites inferior y superior de la integral proveniente de la fórmula de la longitud de arco son
y
Con estos cuatro datos, se realiza la sustitución
Esta integral se resuelve por medio de la sustitución. Así que
Aplicando la sustitución, se tiene que
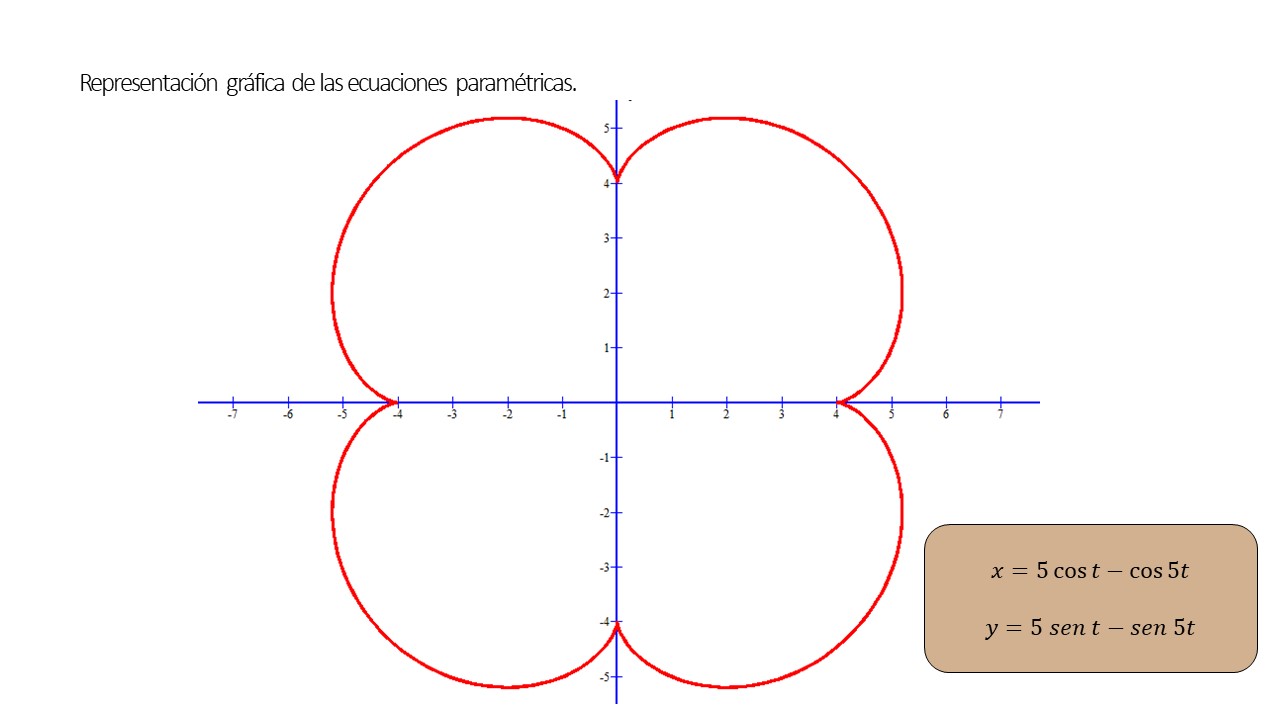
Problema 2. Hallar la longitud de arco mediante las ecuaciones paramétricas:
y
para
Solución. Para poder utilizar la fórmula de la longitud de arco, primero se va derivando la ecuación paramétrica con respecto a
, se tiene lo siguiente
Se aplica el paso anterior para la ecuación paramétrica
Después, del intervalo , los límites inferior y superior de la integral proveniente de la fórmula de la longitud de arco son
y
Con estos cuatro datos, se realiza la sustitución
Finalmente, la longitud de arco de las ecuaciones paramétricas y
para
es de 40 unidades.
Somebody necessarily lend a hand to make significantly posts I might state. This is the very first time I frequented your website page and thus far? I surprised with the analysis you made to make this actual publish incredible. Magnificent job! kdkakdddadde
Me gustaMe gusta
Nice post. I was checking constantly this blog and I am impressed! Extremely useful information specially the last part dedgbbdcbgce
Me gustaMe gusta
Wow, fantastic blog layout! How long have you been blogging for? you make blogging look easy. The overall look of your site is magnificent, as well as the content!
Me gustaMe gusta