Plano tangente y recta normal.
Sea «F» diferenciable en un punto de la superficie S dada por
tal que
.
- Al plano que pasa por P y es normal a
se le llama plano tangente a S a P.
- A la recta que pasa por P y tiene la dirección de
se le llama recta normal a S a P.
Ecuación del plano tangente.
Si F es diferenciable en entonces una ecuación del plano tangente a la superficie dada por
en
es
Problemas resueltos.
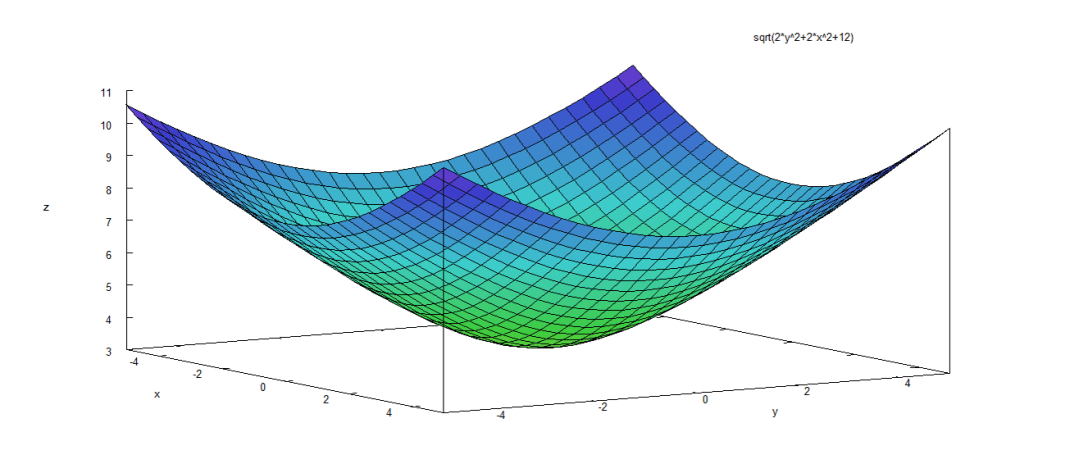
Problema 1. Hallar una ecuación de un plano tangente para
a) y
Solución.
De la función, se debe igualar a cero, así que
Derivando esta función parcialmente con respecto a “x”
con respecto a “y”
con respecto a “z”
Sabiendo que
Así que
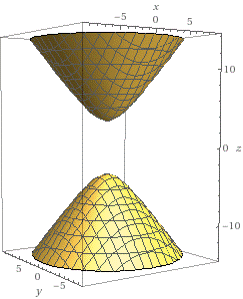
b) en
Solución.
De la función, se debe igualar a cero

Derivando esta función parcialmente con respecto a “x”
Con respecto a “y”
Y con respecto a “z”
Sabiendo que
Así que
Referencias bibliográficas.
- Colley, S. J. (2013). Cálculo vectorial. México: PEARSON EDUCACIÓN.
- Larson, R., & Edwards, B. (2017). Matemáticas 3. Cálculo de varias variables. México: CENGAGE Learning.
- R. Spiegel, M. (1967). Análisis vectorial. México: McGRAW – HILL.
primera vez que leo este proceso bien explicado
Me gustaMe gusta