Circuitos para la retención de datos

En un muestreador convencional, un interruptor se cierra cada período demuestreo T para admitir una señal de entrada. En la práctica, la duración del muestreo es muy corta en comparación con la constante de tiempo más significativa de la planta. Se debe recordar que un muestreador convierte una señal en tiempo continuo en un tren de pulsos que se presenta en los instantes de muestreo t=0, T, 2T, ... , donde T es el período de muestreo. También, si entre dos instantes de muestreo consecutivos el muestreador no transfiere información; dos señales cuyos respectivos valores en los instantes de muestreo son iguales darán como resultado la misma señal muestreada.

La retención de datos es un proceso de generación de una señal en tiempo continuo h(t) a partir de una secuencia en tiempo discreto x(kT). Un circuito de retención convierte la señal muestreada en una señal en tiempo continuo, que reproduce aproximadamente la señal aplicada al muestreador. La señal h(t) durante el intervalo de tiempo kT \le t \le (k+1)T se puede aproximar mediante un polinomio en \tau como sigue:

h(kT + \tau) = a_n {\tau}^n + a_{n-1} {\tau}^{n-1} + ... + a_1 \tau + a_0

donde 0 \le \tau < T. Si la señal h(kT) debe ser igual a x(kT), la ecuación anterior se puede escribir como

h(kT + \tau) = a_n {\tau}^n + a_{n-1} {\tau}^{n-1} + ... + a_1 \tau + x(kT)

Si el circuito de retención de datos es un extrapolador polinomial de n-ésimo orden, se conoce como retenedor de n-ésimo orden. El retenedor de n-ésimo orden emplea n+1 datos discretos anteriores x((k-n)T), x((k-n+1)T), … , x(kT) para generar una señal h(kT+\tau).

Debido a que un retenedor de alto orden utiliza muestras anteriores para extrapolar una señal en tiempo continuo en el instante de muestreo presente y el siguiente, la exactitud en la aproximación de la señal en tiempo continuo se mejora a medida que el número de muestras anteriores utilizadas se incrementa. Sin embargo, esta mejoría se obtiene a costa de un tiempo de retraso mayor. En sistemas de control de lazo cerrado, cualquier tiempo de retardo adicional en el lazo hará una inestabilidad del sistema.

Retenedor de orden cero

El retenedor más sencillo se obtiene cuando n=0, esto es, cuando

h(kT+t) = x(kT)

donde 0 \le \tau < T y k = 0, 1, 2, ... . Esta ecuación implica que el circuito retiene la amplitud de la muestra de un instante muestreo al siguiente. Dicho retenedor de datos se conoce como retenedor de orden cero, o sujetador, o generador de la señal de escalera. La salida del retenedor de orden cero es una función escalonada.

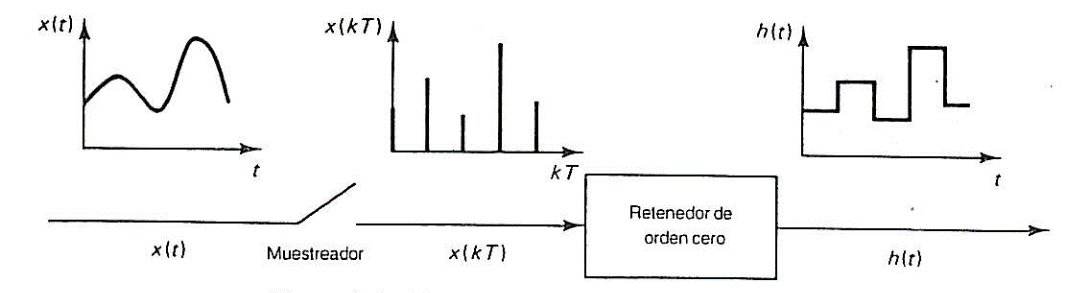
Muestreador y retenedor de orden cero
Figura 1. Muestreador y retenedor de orden cero.

La señal de entrada x(t) se muestrea en instantes discretos y la señal muestreada se pasa a través del retenedor de orden cero. El circuito retenedor de orden cero suaviza la señal muestreada para producir la señal h(t), la cual es constante desde el último valor muestreado hasta que se pueda disponer de la siguiente muestra.

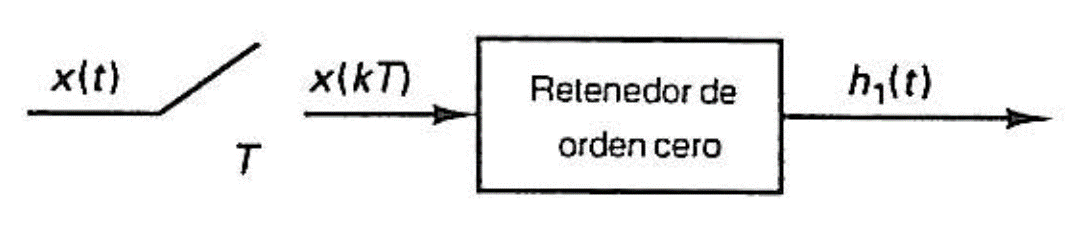
Muestreador real y retenedor de orden cero
Figura 2. Muestreador real y retenedor de orden cero.

Para obtener un modelo matemático de la combinación de un muestreador real y de un circuito de retención de orden cero, comienza a partir del hecho de que la integral de una función impulso es una constante, se puede suponer que el retenedor de orden cero es un integrador, y la entrada al circuito de retención de orden cero es un tren de impulsos. Así que, para el modelo matemático de un muestreador real y un retenedor de orden cero se puede construir de la siguiente manera.

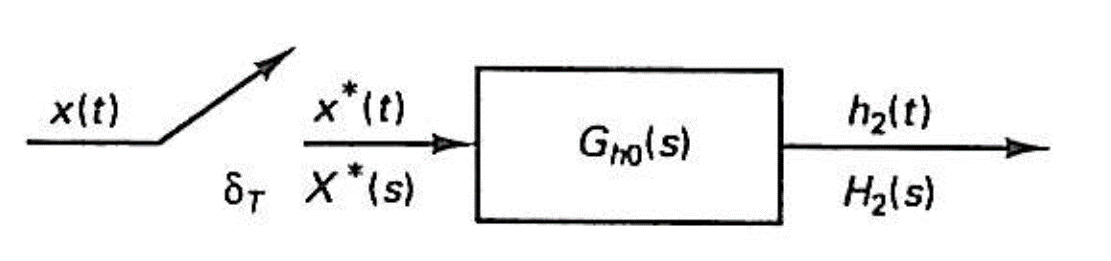
Modelo matemático de un muestreador mediante impulsos y una función de transferencia
Figura 3. Modelo matemático de un muestreador mediante impulsos y una función de transferencia.

El modelo de la figura 3, se observa que G_{h0}(s) representa la función de transferencia del retenedor de orden cero y x^*(t) es la señal muestreada mediante impulsos de x(t).

En base a la figura 2, se va a suponer que la señal x(t) es cero para t<0. Entonces, la salida h_1 (t) está relacionada con x(t) como sigue:

h_1(t) = x(0)[1(t) - 1(t - T)] + x(T)[1(t-T) - 1(t - 2T)] + x(2T)[1(t - 2T) - 1(t - 3T)] + ...

\displaystyle h_1 (t) = \sum_{k=0}^{\infty}{x(kT) \cdot [1(t - kT) - 1(t - (k+1)T]}

Si \displaystyle \mathcal{L} [1(t - kT)] = \frac{e^{-kTs}}{s}, entonces, h_1 (t) tiene la siguiente expresión aplicando transformada de Laplace en ambos miembros

\displaystyle \mathcal{L} [h_1 (t)] = \mathcal{L} \left[\sum_{k=0}^{\infty}{x(kT) \cdot [1(t - kT) - 1(t - (k+1)T]}\right]

\displaystyle \mathcal{L} [h_1 (t)] = \sum_{k=0}^{\infty}{x(kT) \cdot \mathcal{L}[1(t - kT) - 1(t - (k+1)T]}

\displaystyle H_1 (s) = \sum_{k=0}^{\infty}{x(kT) \cdot \left[\frac{e^{-kTs}}{s} - \frac{e^{-(k+1)Ts}}{s}\right]}

\displaystyle H_1 (s) = \left(\frac{1-e^{-Ts}}{s} \right) \sum_{k=0}^{\infty}{x(kT) \cdot e^{-kTs}}

Y en base al modelo matemático en la figura 3, la salida de este modelo debe ser la misma que la del retenedor de orden cero real. luego

\mathcal{L}[h_2(t)] = H_2 (s) = H_1 (s)

Entonces

\displaystyle H_2(s) = \left(\frac{1-e^{-Ts}}{s} \right) \sum_{k=0}^{\infty}{x(kT) \cdot e^{-kTs}}

Además, si las siguientes equivalencias

\displaystyle G_{h0} (s) = \left(\frac{1-e^{-Ts}}{s} \right)    y   \displaystyle X^*(s) = \sum_{k=0}^{\infty}{x(kT) \cdot e^{-kTs}}

se sustituyen en la ecuación H_2(s), se tiene la siguiente expresión

H_2(s) = G_{h0} (s) X^*(s)

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

2 comentarios sobre “Retención de datos y el retenedor de orden cero. Control digital”

Replica a Cesar Reyes Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.