Evaluación de los coeficientes de Fourier por diferenciación. Problemas resueltos. Fourier

Problemas resueltos

Problema 1. Encontrar la serie de Fourier para la forma de onda de la figura 1, hallando la primera derivada de $f(t)$ .

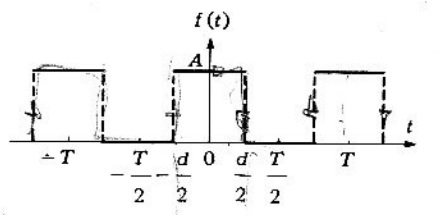
Figura 2.6.1 Forma de onda del problema 1 — *Figura 1. Forma de onda del problema 1.*

Solución. Empezando por la serie de Fourier

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

Se deriva una vez con respecto a $t$ en ambos miembros

$\displaystyle \frac{d}{dt} f(t) = \frac{d}{dt} \left[ \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})} \right]$

$\displaystyle f'(t) = \frac{1}{2} \frac{d}{dt} [a_0] + \sum_{n=1}^{\infty}{\left[\frac{d}{dt}(a_n \cos{n \omega_0 t}) + \frac{d}{dt}(b_n \sin{n \omega_0 t}) \right]}$

$\displaystyle f'(t) = \frac{1}{2} (0) + \sum_{n=1}^{\infty}{\left[ a_n \cdot (-n \omega_0 \sin{n \omega_0 t} ) + b_n \cdot (n \omega_0 \cos{n \omega_0 t}) \right]}$

$\displaystyle f'(t) = \sum_{n=1}^{\infty}{\left( - a_n n \omega_0 \sin{n \omega_0 t} + b_n n \omega_0 \cos{n \omega_0 t} \right)}$

Igualándolo con $\displaystyle f'(t) = \frac{1}{2} \alpha_0 + \sum_{n=1}^{\infty}{(\alpha_n \cos{n \omega_0 t} + \beta_n \sin{n \omega_0 t})}$ , resulta lo siguiente

$\displaystyle f'(t) = \sum_{n=1}^{\infty}{\left( - a_n n \omega_0 \sin{n \omega_0 t} + b_n n \omega_0 \cos{n \omega_0 t} \right)}$

$\displaystyle \frac{1}{2} \alpha_0 + \sum_{n=1}^{\infty}{(\alpha_n \cos{n \omega_0 t} + \beta_n \sin{n \omega_0 t})} = \sum_{n=1}^{\infty}{\left( - a_n n \omega_0 \sin{n \omega_0 t} + b_n n \omega_0 \cos{n \omega_0 t} \right)}$

$\displaystyle \frac{1}{2} \alpha_0 + \sum_{n=1}^{\infty}{(\alpha_n \cos{n \omega_0 t} + \beta_n \sin{n \omega_0 t})} = \sum_{n=1}^{\infty}{\left(b_n n \omega_0 \cos{n \omega_0 t} - a_n n \omega_0 \sin{n \omega_0 t} \right)}$

$\displaystyle \alpha_n \cos{n \omega_0 t} + \beta_n \sin{n \omega_0 t} = b_n n \omega_0 \cos{n \omega_0 t} - a_n n \omega_0 \sin{n \omega_0 t}$

Donde $\alpha_n = b_n n \omega_0$ y $\beta_n = - a_n n \omega_0$ .

Despejando $a_n$

$\displaystyle a_n = - \frac{\beta_n}{n \omega_0}$

Despejando $b_n$

$\displaystyle b_n = \frac{\alpha_n}{n \omega_0}$

Graficando la primera derivada de la forma de onda brindada por el problema 1, se tiene que

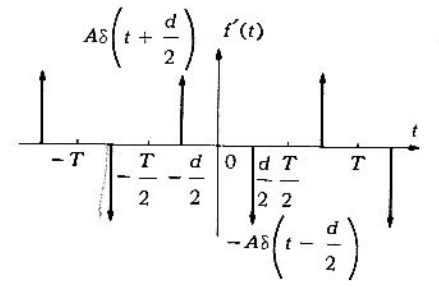
Figura 2.6.2 La primera derivada de la forma de onda del problema 1 — *Figura 2. La primera derivada de la forma de onda del problema 1.*

Y como $f'(t)$ es una función generalizada impar, el valor de $\alpha_n = 0$ para todo $n=1,2,3, \cdots$ mientras que el valor de $\beta_n$ es

$\displaystyle \beta_n = \frac{4}{T} \int_{0}^{T/2}{f'(t) \sin{n \omega_0 t} \, dt}$

$\displaystyle \beta_n = \frac{4}{T} \int_{0}^{T/2}{\left[- A \delta \left(t - \frac{d}{2} \right) \right] \sin{n \omega_0 t} \, dt}$

$\displaystyle \beta_n = - \frac{4A}{T} \int_{0}^{T/2}{\sin{n \omega_0 t} \cdot \delta \left(t - \frac{d}{2} \right) \, dt}$

$\displaystyle \beta_n = - \left. \frac{4A}{T} \sin{n \omega_0 t} \right|_{t=d/2} = - \frac{4A}{T} \sin{n \omega_0 \cdot \frac{d}{2}}$

$\displaystyle \beta_n = - \frac{4A}{T} \sin{\frac{n \omega_0 d}{2}}$

Sustituyendo con el valor de $a_n$ , resulta

$\displaystyle a_n = - \frac{\beta_n}{n \omega_0}$

$\displaystyle a_n = - \frac{\left(- \frac{4A}{T} \sin{\frac{n \omega_0 d}{2}} \right)}{n \omega_0}$

$\displaystyle a_n = \frac{\frac{4A}{T} \sin{\frac{n \omega_0 d}{2}}}{n \omega_0}$

$\displaystyle a_n = \frac{4A}{n T \omega_0} \sin{\frac{n \omega_0 d}{2}} = \frac{4A}{n T \omega_0} \cdot \frac{\frac{n\omega_0 d}{2}}{\frac{n\omega_0 d}{2}} \cdot \sin{\frac{n \omega_0 d}{2}}$

$\displaystyle a_n = \frac{4A}{n T \omega_0} \cdot \frac{n\omega_0 d}{2} \cdot \frac{\sin{\frac{n \omega_0 d}{2}}}{\frac{n\omega_0 d}{2}}$

$\displaystyle \therefore a_n = \frac{2Ad}{T} \cdot \frac{\sin{\frac{n \omega_0 d}{2}}}{\frac{n\omega_0 d}{2}}$

Sustituyendo con el valor de $b_n$ , resulta

$\displaystyle b_n = \frac{\alpha_n}{n \omega_0}$

$\displaystyle b_n = \frac{0}{n \omega_0}$

$\therefore b_n = 0$

En el caso de $a_0$ , fue eliminado durante la diferenciación, pero

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{-d/2}{(0) \, dt} + \frac{2}{T} \int_{-d/2}^{d/2}{A \, dt} + \frac{2}{T} \int_{d/2}^{T/2}{(0) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \int_{-d/2}^{d/2}{A \, dt} = \frac{2A}{T} \int_{-d/2}^{d/2}{dt}$

$\displaystyle a_0 = \frac{2A}{T} [t+C]_{-d/2}^{d/2} = \frac{2A}{T} \left[\frac{d}{2} - (-\frac{d}{2}) \right]$

$\displaystyle a_0 = \frac{2A}{T} \left(\frac{d}{2} + \frac{d}{2} \right) = \frac{2A}{T} \left(d \right)$

$\displaystyle \therefore a_0 = \frac{2Ad}{T}$

Y la serie de Fourier es

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

$\displaystyle f(t) = \frac{1}{2} \cdot \frac{2Ad}{T} + \sum_{n=1}^{\infty}{\left(\frac{2Ad}{T} \cdot \frac{\sin{\frac{n \omega_0 d}{2}}}{\frac{n\omega_0 d}{2}} \cdot \cos{n \omega_0 t} + (0) \sin{n \omega_0 t}\right)}$

$\displaystyle f(t) = \frac{Ad}{T} + \sum_{n=1}^{\infty}{\left(\frac{2Ad}{T} \cdot \frac{\sin{\frac{n \omega_0 d}{2}}}{\frac{n\omega_0 d}{2}} \cdot \cos{n \omega_0 t} \right)}$

$\displaystyle \therefore f(t) = \frac{Ad}{T} + \frac{2Ad}{T} \sum_{n=1}^{\infty}{\left(\frac{\sin{\frac{n \omega_0 d}{2}}}{\frac{n\omega_0 d}{2}} \cdot \cos{n \omega_0 t} \right)}$

Problema 2. Encontrar la serie de Fourier para la forma de onda de la siguiente figura por diferenciación.

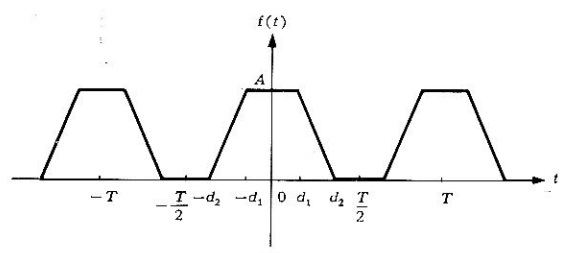
Figura 2.6.3 Forma de onda del problema 2 — *Figura 3. Forma de onda del problema 2.*

Solución. Si $f(t)$ se desarrolla en una serie de Fourier

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

Se puede determinar su primera derivada

$\displaystyle \frac{d}{dt} f(t) = \frac{d}{dt} \left[ \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})} \right]$

$\displaystyle f'(t) = \frac{1}{2} \frac{d}{dt} [a_0] + \sum_{n=1}^{\infty}{\left[\frac{d}{dt}(a_n \cos{n \omega_0 t}) + \frac{d}{dt}(b_n \sin{n \omega_0 t}) \right]}$

$\displaystyle f'(t) = \frac{1}{2} (0) + \sum_{n=1}^{\infty}{\left[ a_n \cdot (-n \omega_0 \sin{n \omega_0 t} ) + b_n \cdot (n \omega_0 \cos{n \omega_0 t}) \right]}$

$\displaystyle f'(t) = \sum_{n=1}^{\infty}{\left( - a_n n \omega_0 \sin{n \omega_0 t} + b_n n \omega_0 \cos{n \omega_0 t} \right)}$

En base a este resultado, se muestra en la siguiente gráfica (figura 4)

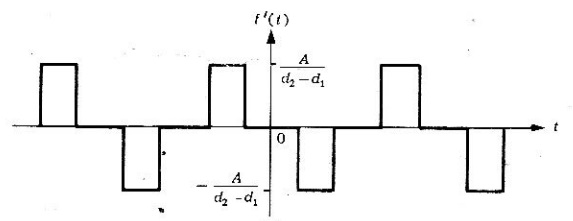
Figura 2.6.4 Primera derivada de la forma de onda del problema 2 — *Figura 4. Primera derivada de la forma de onda del problema 2.*

Determinado su segunda derivada

$\displaystyle \frac{d}{dt} [f'(t)] = \frac{d}{dt} \left[ \sum_{n=1}^{\infty}{\left( - a_n n \omega_0 \sin{n \omega_0 t} + b_n n \omega_0 \cos{n \omega_0 t} \right)} \right]$

$\displaystyle f''(t) = \sum_{n=1}^{\infty}{\left[ \frac{d}{dt} \left( - a_n n \omega_0 \sin{n \omega_0 t} \right) + \frac{d}{dt} \left(b_n n \omega_0 \cos{n \omega_0 t} \right) \right]}$

$\displaystyle f''(t) = \sum_{n=1}^{\infty}{\left[- a_n (n \omega_0)^2 \cos{n \omega_0 t} - b_n (n \omega_0)^2 \sin{n \omega_0 t} \right]}$

Y de este resultado, se muestra la siguiente gráfica (figura 5)

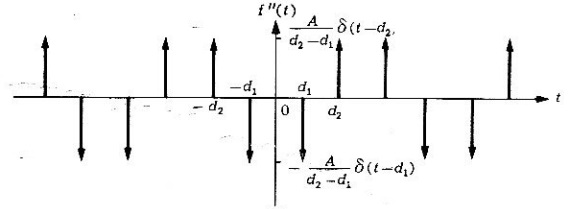
Figura 2.6.5 Una función par generalizada f''(t) de f(t) — *Figura 5. Una función par generalizada f»(t) de f(t).*

Al igualarlo con $\displaystyle f''(t) = \frac{1}{2} \alpha_0 + \sum_{n=1}^{\infty}{(\alpha_n \cos{n \omega_0 t} + \beta_n \sin{n \omega_0 t})}$ , se tiene lo siguiente

$\displaystyle f''(t) = \sum_{n=1}^{\infty}{\left[- a_n (n \omega_0)^2 \cos{n \omega_0 t} - b_n (n \omega_0)^2 \sin{n \omega_0 t} \right]}$

$\displaystyle \frac{1}{2} \alpha_0 + \sum_{n=1}^{\infty}{(\alpha_n \cos{n \omega_0 t} + \beta_n \sin{n \omega_0 t})} = \sum_{n=1}^{\infty}{\left[- a_n (n \omega_0)^2 \cos{n \omega_0 t} - b_n (n \omega_0)^2 \sin{n \omega_0 t} \right]}$

Observando que $\alpha = 0$ , $\alpha_n = - a_n (n \omega_0)^2$ y $\beta_n = - b_n (n \omega_0)^2$ . Despejando $a_n$ , resulta

$\displaystyle \alpha_n = - a_n (n \omega_0)^2$

$\displaystyle - \frac{\alpha_n}{(n \omega_0)^2} = a_n$

$\displaystyle a_n = - \frac{\alpha_n}{(n \omega_0)^2}$

Despejando $b_n$ , resulta

$\displaystyle \beta_n = - b_n (n \omega_0)^2$

$\displaystyle - \frac{\beta_n}{(n \omega_0)^2} = b_n$

$\displaystyle b_n = - \frac{\beta_n}{(n \omega_0)^2}$

Por medio de la figura 5, $f''(t)$ es una función par generalizada

$\displaystyle f''(t) = \frac{A}{d_2 - d_1} [- \delta (t- d_1) + \delta (t - d_2)]$

en $\displaystyle 0 < t < \frac{T}{2}$ .

Calculando $\alpha_n$

$\displaystyle \alpha_n = \frac{4}{T} \int_{0}^{T/2}{f''(t) \cos{n \omega_0 t} \, dt}$

$\displaystyle \alpha_n = \frac{4A}{T(d_2 - d_1)} \int_{0}^{T/2}{[- \delta (t- d_1) + \delta (t - d_2)] \cos{n \omega_0 t} \, dt}$

$\displaystyle \alpha_n = - \frac{4A}{T(d_2 - d_1)} \int_{0}^{T/2}{\delta (t- d_1) \cos{n \omega_0 t} \, dt} + \frac{4A}{T(d_2 - d_1)} \int_{0}^{T/2}{\delta (t - d_2) \cos{n \omega_0 t} \, dt}$

$\displaystyle \alpha_n = - \frac{4A}{T(d_2 - d_1)} \cos{n \omega_0 d_1} + \frac{4A}{T(d_2 - d_1)} \cos{n \omega_0 d_2}$

$\displaystyle \alpha_n = \frac{4A}{T(d_2 - d_1)} (- \cos{n \omega_0 d_1} + \cos{n \omega_0 d_2})$

Y el valor de $\beta_n$

$\beta_n = 0$

debido a que la función es par.

Entonces, el valor de $a_n$ es

$\displaystyle a_n = - \frac{\alpha_n}{(n \omega_0)^2}$

$\displaystyle a_n = - \frac{\frac{4A}{T(d_2 - d_1)} (- \cos{n \omega_0 d_1} + \cos{n \omega_0 d_2})}{(n \omega_0)^2}$

$\displaystyle a_n = - \frac{4A}{(n \omega_0)^2 T (d_2 - d_1)} (- \cos{n \omega_0 d_1} + \cos{n \omega_0 d_2})$

$\displaystyle a_n = - \frac{4A}{n^2 \omega_0^2 T (d_2 - d_1)} (- \cos{n \omega_0 d_1} + \cos{n \omega_0 d_2})$

$\displaystyle a_n = - \frac{4A}{n^2 \cdot \frac{4\pi^2}{T^2} T (d_2 - d_1)} (- \cos{n \omega_0 d_1} + \cos{n \omega_0 d_2})$

$\displaystyle a_n = - \frac{A T}{n^2 \pi^2 (d_2 - d_1)} (- \cos{n \omega_0 d_1} + \cos{n \omega_0 d_2})$

$\displaystyle a_n = \frac{A T}{n^2 \pi^2 (d_2 - d_1)} (\cos{n \omega_0 d_1} - \cos{n \omega_0 d_2})$

El valor de $b_n$ es

$\displaystyle b_n = - \frac{\beta_n}{(n \omega_0)^2}$

$\displaystyle b_n = - \frac{0}{(n \omega_0)^2}$

$\displaystyle b_n = 0$

Y el valor de $a_0$ es

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{T/2}{f(t) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \int_{-T/2}^{-d_2}{(0) \, dt} + \frac{2}{T} \int_{-d_2}^{-d_1}{\frac{A}{-d_1 + d_2} (t + d_2) \, dt} + \frac{2}{T} \int_{-d_1}^{d_1}{A \, dt}$

$\displaystyle + \frac{2}{T} \int_{d_1}^{d_2}{[A - \frac{A}{d_2 - d_1} (t - d_1)] \, dt} + \frac{2}{T} \int_{d_2}^{T/2}{(0) \, dt}$

$\displaystyle a_0 = \frac{2}{T} \int_{-d_2}^{-d_1}{\frac{A}{-d_1 + d_2} (t + d_2) \, dt} + \frac{2}{T} \int_{-d_1}^{d_1}{A \, dt} + \frac{2}{T} \int_{d_1}^{d_2}{[A - \frac{A}{d_2 - d_1} (t - d_1)] \, dt}$

$\displaystyle a_0 = \frac{2A}{T(-d_1 + d_2)} \int_{-d_2}^{-d_1}{(t + d_2) \, dt} + \frac{2A}{T} \int_{-d_1}^{d_1}{dt} + \frac{2A}{T} \int_{d_1}^{d_2}{dt} - \frac{2A}{T(d_2 - d_1)} \int_{d_1}^{d_2}{(t - d_1) \, dt}$

$\displaystyle a_0 = \frac{2A}{T(d_2 - d_1)} \int_{-d_2}^{-d_1}{(t + d_2) \, dt} + \frac{2A}{T} \int_{-d_1}^{d_2}{dt} - \frac{2A}{T(d_2 - d_1)} \int_{d_1}^{d_2}{(t - d_1) \, dt}$

$\displaystyle a_0 = \frac{2A}{T(d_2 - d_1)} \left[\frac{1}{2} t^2 + d_2 t +C \right]_{-d_2}^{- d_1} + \frac{2A}{T} \left[t + C \right]_{-d_1}^{d_2} - \frac{2A}{T(d_2 - d_1)} \left[\frac{1}{2} t^2 - d_1 t +C \right]_{d_1}^{d_2}$

$\displaystyle a_0 = \frac{2A}{T(d_2 - d_1)} \left(\frac{1}{2} d_1^2 - d_1 d_2 - \frac{1}{2} d_2^2 + d_2^2 \right) + \frac{2A}{T} \left(d_2 + d_1 \right) - \frac{2A}{T(d_2 - d_1)} \left(\frac{1}{2} d_2^2 - d_1 d_2 - \frac{1}{2} d_1^2 + d_1^2 \right)$

$\displaystyle a_0 = \frac{2A}{T(d_2 - d_1)} \left(\frac{1}{2} d_1^2 - d_1 d_2 - \frac{1}{2} d_2^2 + d_2^2 - \frac{1}{2} d_2^2 + d_1 d_2 + \frac{1}{2} d_1^2 - d_1^2 \right) + \frac{2A}{T} \left(d_2 + d_1 \right)$

$\displaystyle a_0 = \frac{2A}{T} \left(d_2 + d_1 \right)$

Sustituyendo en la serie de Fourier, se obtiene el resultado final

$\displaystyle f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}{(a_n \cos{n \omega_0 t} + b_n \sin{n \omega_0 t})}$

$\displaystyle f(t) = \frac{1}{2} \cdot \frac{2A}{T} (d_2 + d_1) + \sum_{n=1}^{\infty}{\left[\frac{A T}{n^2 \pi^2 (d_2 - d_1)} (\cos{n \omega_0 d_1} - \cos{n \omega_0 d_2}) \cdot \cos{n \omega_0 t} + (0) \sin{n \omega_0 t} \right]}$

$\displaystyle \therefore f(t) = \frac{A}{T} (d_2 + d_1) + \frac{A T}{\pi^2 (d_2 - d_1)} \sum_{n=1}^{\infty}{\frac{1}{n^2} (\cos{n \omega_0 d_1} - \cos{n \omega_0 d_2}) \cos{n \omega_0 t} }$

Un comentario sobre “Evaluación de los coeficientes de Fourier por diferenciación. Problemas resueltos. Fourier”

Angelilie dice:

18 agosto, 2018 a las 10:06 am

J’aime beaucoup votre blog. Un plaisir de venir flâner sur vos pages. Une belle découverte et blog très intéressant. Je reviendrai m’y poser. N’hésitez pas à visiter mon univers. Au plaisir

Me gustaMe gusta

Responder

Replica a Angelilie Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.

Evaluación de los coeficientes de Fourier por diferenciación. Problemas resueltos. Fourier

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Un comentario sobre “Evaluación de los coeficientes de Fourier por diferenciación. Problemas resueltos. Fourier”

Replica a Angelilie Cancelar la respuesta