Espectros de frecuencia compleja. Fourier.

Introducción

La gráfica de la magnitud de los coeficientes complejos $c_n$ en la serie

$f(t) = \sum_{n=-\infty}^{\infty}{c_n e^{j n \omega_0 t}}$ ,

versus la frecuencia $\omega$ (frecuencia angular), se denomina espectro de amplitud de la función periódica $f(t)$ . La gráfica del ángulo de fase $\phi_n$ de $c_n$ versus $\omega$ ( $\displaystyle c_n = |c_n| e^{j \phi n}$ y $\displaystyle c_{-n} = c_{n}^* = |c_n| e^{-j \phi_n}$ ), se denomina espectro de fase de $f(t)$ . Puesto que índice $n$ toma solamente valores enteros, los espectros de amplitud y fase no son curvas continuas sino que aparece en la variable discreta $n\omega_0$ ; por consiguiente, se les denomina como espectros de frecuencia discreta o espectros de línea. La representación de los coeficientes complejos $c_n$ versus la variable discreta $n\omega_0$ , especifica la función periódica $f(t)$ en el dominio la frecuencia, así como $f(t)$ versus $t$ especifica la función en el dominio del tiempo.

Problemas resueltos

Problema 1. Encontrar los espectros de frecuencia para la función periódica $f(t)$ , que se muestra en la figura 1, la cual consta de un tren de pulsos rectangulares idénticos de magnitud $A$ y duración $d$ .

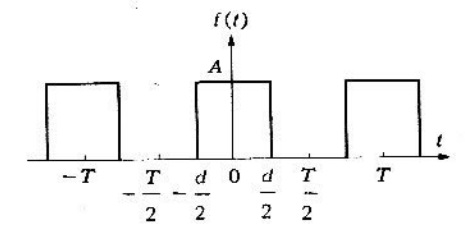
Figura 3.3.1 Tren de pulsos rectangulares idénticos — *Figura 1. Tren de pulsos rectángulares idénticos.*

Solución. En un período, la función $f(t)$ se puede expresar de la siguiente manera

$\displaystyle f(t) = \left\{ \begin{matrix} A \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad -d/2 < t < d/2\\0 \quad \quad -T/2 < t < -d/2, \quad \quad d/2 < t < T/2 \end{matrix} \right.$

Calculando el coeficiente $c_n$ , resulta

$\displaystyle c_n = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{1}{T} \int_{-T/2}^{-d/2}{(0) e^{-jn\omega_0 t} \, dt} + \frac{1}{T} \int_{-d/2}^{d/2}{(A) e^{-jn\omega_0 t} \, dt} + \frac{1}{T} \int_{d/2}^{T/2}{(0) e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{A}{T} \int_{-d/2}^{d/2}{e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{A}{T} \left[-\frac{1}{jn\omega_0} e^{-jn\omega_0 t} \right]_{-d/2}^{d/2}$

$\displaystyle c_n = \frac{A}{T} \left[-\frac{1}{jn\omega_0} e^{-jn\omega_0 \left( \frac{d}{2} \right)} + \frac{1}{jn\omega_0} e^{-jn\omega_0 \left(- \frac{d}{2} \right)} \right]$

$\displaystyle c_n = \frac{A}{jn \omega_0 T} \left[-e^{-jn\omega_0 \left( \frac{d}{2} \right)} + e^{-jn\omega_0 \left(- \frac{d}{2} \right)} \right]$

$\displaystyle c_n = \frac{A}{jn \omega_0 T} \left[-e^{-jn\omega_0 \left( \frac{d}{2} \right)} + e^{jn\omega_0 \left(\frac{d}{2} \right)} \right]$

$\displaystyle c_n = \frac{A}{jn \omega_0 T} \cdot \frac{2}{2} \left[-e^{-jn\omega_0 \left( \frac{d}{2} \right)} + e^{jn\omega_0 \left(\frac{d}{2} \right)} \right]$

$\displaystyle c_n = \frac{2A}{n \omega_0 T} \left[\frac{-e^{-jn\omega_0 \left( \frac{d}{2} \right)} + e^{jn\omega_0 \left(\frac{d}{2} \right)}}{j2} \right]$

$\displaystyle c_n = \frac{2A}{n \omega_0 T} \left[\frac{e^{jn\omega_0 \left(\frac{d}{2} \right)} -e^{-jn\omega_0 \left( \frac{d}{2} \right)}}{j2} \right]$

$\displaystyle c_n = \frac{2A}{n \omega_0 T} \left[ \sin{\left( \frac{n \omega_0 d}{2} \right)} \right] = \frac{2A}{n \omega_0 T} \cdot \frac{\frac{d}{2}}{\frac{d}{2}} \left[ \sin{\left( \frac{n \omega_0 d}{2} \right)} \right]$

$\displaystyle c_n = \frac{2A \frac{d}{2}}{n \omega_0 T \frac{d}{2}} \left[ \sin{\left( \frac{n \omega_0 d}{2} \right)} \right] = \frac{Ad}{T \frac{n \omega_0 d}{2}} \left[ \sin{\left( \frac{n \omega_0 d}{2} \right)} \right]$

$\displaystyle c_n = \frac{Ad}{T} \left[ \frac{\sin{\left( \frac{n \omega_0 d}{2} \right)}}{\frac{n \omega_0 d}{2}} \right] = \frac{Ad}{T} \left[ \frac{\sin{\left( \frac{n \frac{2\pi}{T} d}{2} \right)}}{\frac{n \frac{2\pi}{T} d}{2}} \right]$

$\displaystyle c_n = \frac{Ad}{T} \left[ \frac{\sin{\left( \frac{n \pi d}{T} \right)}}{\frac{n \pi d}{T}} \right]$

El resultado $c_n$ solo tiene parte real, por tanto, el espectro de frecuencia de fase es cero. El espectro de amplitud se obtiene dibujando con el resultado de $c_n$ versus la variable discreta $n \omega_0$ . El resultado de $c_n$ tiene valores solamente para la frecuencia discreta $n\omega_0$ ; es decir, el espectro de frecuencia es una función discreta y existe solamente cuando

$\displaystyle \omega = 0, \, \frac{\pm 2 \pi}{T}, \, \frac{\pm 4 \pi}{T}, \, \cdots$

Se debe considerar el espectro para algunos valores específicos de $d \, t \, T$ ; para $d=1/20$ y $T=1/4$ de segundo,

$\displaystyle \omega = \frac{2\pi}{T} = \frac{2\pi}{\frac{1}{4}} = 8 \pi$

Luego, el espectro de amplitud existe cuando

$\displaystyle \omega = 0, \, \pm 8\pi, \, \pm 16 \pi. \, \pm 32 \pi, \, \cdots$

y se muestra en la gráfica 2.

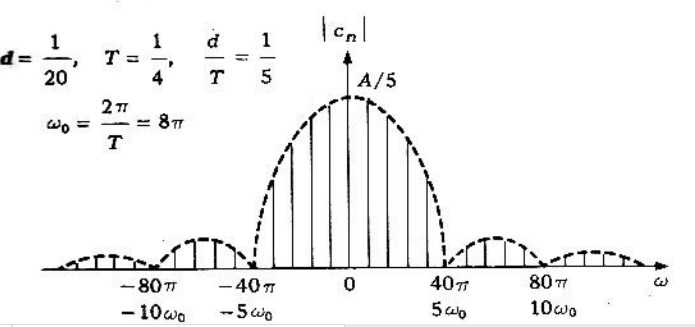
Figura 3.3.2 Espectros de amplitud — *Figura 2. Espectros de amplitud para d=1/20 y T=1/4.*

Como $d/T = (1/20)/(1/4) = 1/5$ , el espectro de amplitud se hace cero en el valor de $n \omega_0$ , para el cual

$\displaystyle n \omega_0 \frac{d}{2} = m \pi$

$\displaystyle n \frac{2\pi}{T} \frac{d}{2} = m \pi$

$\displaystyle n \frac{2\pi}{2} \frac{d}{T} = m \pi$

$\displaystyle n \pi \frac{1}{5} = m \pi$

donde $m = \pm 1, \, \pm 2, \, \cdots$ , es decir, cuando $\omega = \pm 5 \omega_0 = \pm 40 \pi, \, \pm 10 \omega_0 = \pm 80 \pi, \, \pm 15 \omega_0 = \pm 120 \pi, \, \cdots$ . Ahora, se considerará $d=1/20$ y $T=1/2$ de segundo, y

$\displaystyle \omega = \frac{2\pi}{T} = \frac{2\pi}{1/2} = 4\pi$

$\displaystyle \frac{d}{T} =\frac{(1/20)}{(1/2)} = \frac{1}{10}$

Después, el espectro de magnitud existe cuando

$\displaystyle \omega = 0, \, \pm 4 \pi, \, \pm 8 \pi, \, \cdots$

y se hace cero en el valor de $n \omega_0$ para el cual

$\displaystyle n \omega_0 \frac{d}{2} = m \pi$

$\displaystyle n \frac{2\pi}{T} \frac{d}{2} = m \pi$

$\displaystyle n \frac{2\pi}{2} \frac{d}{T} = m \pi$

$\displaystyle n \pi \frac{1}{10} = m \pi$

para $m=\pm 1, \pm 2, \pm 3, \cdots$ , es decir, cuando $\omega = \pm 10 \omega_0 = \pm 40 \pi, \, \pm 20 \omega_0 = \pm 80 \pi, \, \pm 30 \omega_0 = \pm 120 \pi, \, \cdots$ . El espectro de amplitud para este caso se muestra en el figura 3.

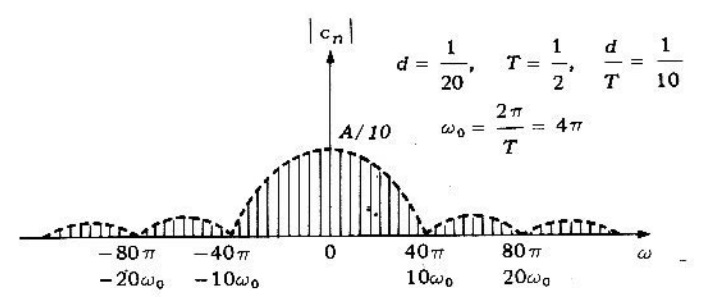
Figura 3.3.3 Espectros de amplitud — *Figura 3. Espectro de amplitud para d=1/20, T=1/2.*

Problema 2. Encontrar los espectros de frecuencia de la función periódica que se muestra en la siguiente figura

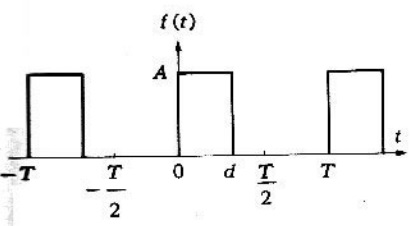
Figura 3.3.4. Función f(t) del problema P2 — *Figura 4. Función f(t) del problema P2.*

Solución. La función está definida

$\displaystyle f(t) = \left\{ \begin{matrix} A, \quad 0 < t < d\\0, \quad d < t < T \end{matrix} \right.$

Calculando el coeficiente $c_n$ (observando que en la figura 3.3.4 el período es $T$ )

$\displaystyle c_n = \frac{1}{T} \int_{0}^{T}{f(t) e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{1}{T} \int_{0}^{d}{(A) e^{-jn\omega_0 t} \, dt} + \frac{1}{T} \int_{d}^{T}{(0) e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{1}{T} \int_{0}^{d}{(A) e^{-jn\omega_0 t} \, dt} = \frac{A}{T} \int_{0}^{d}{e^{-jn\omega_0 t} \, dt}$

$\displaystyle c_n = \frac{A}{T} \left[\left(- \frac{1}{j n \omega_0} \right) e^{-jn\omega_0 t} \right]_{0}^{d}$

$\displaystyle c_n = \frac{A}{T} \left[\left(- \frac{1}{j n \omega_0} \right) e^{-jn\omega_0 (d)} - \left(- \frac{1}{j n \omega_0} \right) e^{-jn\omega_0 (0)} \right]$

$\displaystyle c_n = \frac{A}{T} \left[\left(- \frac{1}{j n \omega_0} \right) e^{-jn\omega_0 d} - \left(- \frac{1}{j n \omega_0} \right) \right]$

$\displaystyle c_n = \frac{A}{T} \left[- \left(\frac{1}{j n \omega_0} \right) e^{-jn\omega_0 d} + \left(\frac{1}{j n \omega_0} \right) \right]$

$\displaystyle c_n = \frac{A}{j n \omega_0 T} \left(- e^{-jn\omega_0 d} + 1 \right) = \frac{A}{j n \omega_0 T} \left(1 - e^{-jn\omega_0 d}\right)$

$\displaystyle c_n = \frac{A}{j n \omega_0 T} \cdot \frac{e^{j n \omega_0 d/2}}{e^{j n \omega_0 d/2}} \left(1 - e^{-jn\omega_0 d}\right)$

$\displaystyle c_n = \frac{A}{j n \omega_0 T} \cdot \frac{1}{e^{j n \omega_0 d/2}} \left(e^{j n \omega_0 d/2} - e^{-jn\omega_0 d/2}\right)$

$\displaystyle c_n = \frac{A}{j n \omega_0 T} \cdot \frac{1}{e^{j n \omega_0 d/2}} \cdot \frac{j2}{j2} \left(e^{j n \omega_0 d/2} - e^{-jn\omega_0 d/2}\right)$

$\displaystyle c_n = \frac{A}{j n \omega_0 T} \cdot \frac{j2}{e^{j n \omega_0 d/2}} \left( \frac{e^{j n \omega_0 d/2} - e^{-jn\omega_0 d/2}}{j2} \right)$

$\displaystyle c_n = \frac{2A}{n \omega_0 T} \cdot \frac{1}{e^{j n \omega_0 d/2}} \sin{\frac{n \omega_0 d}{2}}$

$\displaystyle c_n = \frac{2A}{n \omega_0 T} e^{-j n \omega_0 d/2} \sin{\frac{n \omega_0 d}{2}}$

$\displaystyle c_n = \frac{2A}{n \omega_0 T} \sin{\frac{n \omega_0 d}{2}} \cdot e^{-j n \omega_0 d/2}$

$\displaystyle c_n = \frac{2A}{n \omega_0 T} \sin{\frac{n \omega_0 d}{2}} \cdot \frac{\frac{n \omega_0 d}{2}}{\frac{n \omega_0 d}{2}} \cdot e^{-j n \omega_0 d/2}$

$\displaystyle c_n = \frac{2A \cdot \frac{n \omega_0 d}{2}}{n \omega_0 T} \cdot \frac{ \sin{\frac{n \omega_0 d}{2}} }{\frac{n \omega_0 d}{2}} \cdot e^{-j n \omega_0 d/2}$

$\displaystyle c_n = \frac{Ad}{T} \cdot \frac{ \sin{\frac{n \omega_0 d}{2}} }{\frac{n \omega_0 d}{2}} \cdot e^{-j n \omega_0 d/2}$

Recordando que $c_n = |c_n| e^{j \phi_n}$ , se tiene que

$\displaystyle \therefore |c_n| = \frac{Ad}{T} \cdot \frac{ \sin{\frac{n \omega_0 d}{2}} }{\frac{n \omega_0 d}{2}}$

$\displaystyle \therefore \phi_n = - \frac{n \omega_0 d}{2}$

El espectro de amplitud no se ve afectado por el cambio de origen, pero el espectro de fase es, ahora, igual a $-n\omega_0 d/2 = - n\pi d/T$ radianes.

Problema 3. Demostrar que el desplazamiento en el tiempo de una función periódica no tiene efecto sobre el espectro de magnitud, pero modifica el espectro de fase en una cantidad de $-n \omega_0 \tau$ radianes para la componente de frecuencia $n \omega_0$ si el desplazamiento en el tiempo es $\tau$ .

Solución. Sea $f(t)$ una función periódica con período $T$ , y sea su serie de Fourier dada por

$\displaystyle f(t) = \sum_{n=- \infty}^{\infty}{c_n e^{jn \omega_0 t}}$

Después

$\displaystyle f(t - \tau) = \sum_{n=- \infty}^{\infty}{c_n e^{jn \omega_0 (t - \tau)}}$

$\displaystyle f(t - \tau) = \sum_{n=- \infty}^{\infty}{c_n e^{jn \omega_0 t} e^{- j n \omega_0 \tau}}$

$\displaystyle f(t - \tau) = \sum_{n=- \infty}^{\infty}{c_n e^{- j n \omega_0 \tau} e^{jn \omega_0 t}}$

$\displaystyle f(t - \tau) = \sum_{n=- \infty}^{\infty}{c_n^{'} e^{jn \omega_0 t}}$

donde $c_n^{'} = c_n e^{- j n \omega_0 \tau}$ . Luego, si

$c_n = |c_n| e^{j \phi_n}$

– – – – – (1)

Entonces

$c_n = |c_n| e^{j \phi_n} e^{- j n \omega_0 \tau}$

$c_n = |c_n| e^{j \phi_n - j n \omega_0 \tau}$

$\therefore c_n = |c_n| e^{j n (\phi_n - \omega_0 \tau)}$

– – – – – (2)

Las ecuaciones (1) y (2), se observan que el espectro de magnitud de $f(t)$ y $f(t-\tau)$ es el mismo; sin embargo, las fases son diferentes. El desplazamiento en un tiempo $\tau$ produce un atraso de $n \omega_0 t$ radianes en la componente de frecuencia $n \omega_0$ .

Del resultado $c_n$ del problema 1, $\displaystyle c_n = \frac{Ad}{T} \left[ \frac{\sin{\left( \frac{n \pi d}{T} \right)}}{\frac{n \pi d}{T}} \right]$ , si

$\displaystyle \frac{n \omega_0 d}{2} = \frac{n \pi d}{2} = \frac{n \pi d}{T} = x_n$

entonces

$\displaystyle c_n = \frac{Ad}{T} \left( \frac{\sin{x_n}}{x_n} \right)$

La envolvente de $c_n$ es una función continua, la cual se encuentra reemplazando $n\omega_0$ por $\omega$ , o reemplazando $x_n$ por $x$ . En análisis frecuencial, la función

$\displaystyle Sa (x) = \frac{\sin{x}}{x}$

desempeña un papel importante y se conoce como la función de muestro, cuya gráfica se ilustra en la figura 5. Se debe notar que la función tiene ceros cuando $x = \pm n \pi$ , cuando $n =1,2,3, \cdots$ , etc.