Evaluación de los coeficientes complejos de Fourier por medio de la función δ. Fourier.

Problemas resueltos

Problema 1. Deducir la serie compleja de Fourier, de tren periódico de impulsos unitarios de la figura 3.4.1.

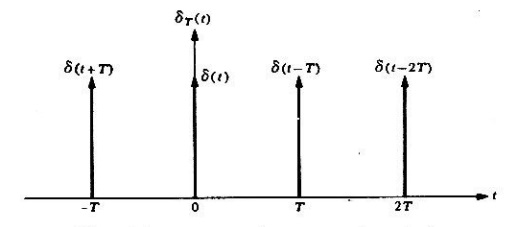
*Figura 3.4.1 Tren periódico de impulsos unitarios.*

Solución. Un tren periódico $\displaystyle \delta_T (t)$ de implusos unitarios se puede expresar como

$\displaystyle \large \delta_T (t) = \left\{ \begin{matrix} \sum_{n=- \infty}^{\infty}{\delta_T (t - nT)} & , & -T/2 < t < T/2 \\ \\ \delta (t) & , & -T/2 < t < T/2 \end{matrix} \right.$

Después, con $\omega_0 = 2\pi/T$ , se tiene lo siguiente

$\displaystyle c_n = \frac{1}{T} \int_{-T/2}^{T/2}{\delta_T (t) e^{-j n \omega_0 t} \, dt}$

$\displaystyle c_n = \frac{1}{T} \int_{-T/2}^{T/2}{\delta (t) e^{-j n \omega_0 t} \, dt} = \frac{1}{T} \left. e^{-j n \omega_0 t}\right|_{t=0}$

$\displaystyle c_n = \frac{1}{T} e^{-j n \omega_0 (0)} = \frac{1}{T}(1)$

$\displaystyle c_n = \frac{1}{T}$

Finalmente

$\displaystyle f(t) = \sum_{n=-\infty}^{\infty}{c_n e^{-j n \omega_0 t}}$

$\displaystyle \delta_T (t) = \sum_{n=-\infty}^{\infty}{c_n e^{-j n \omega_0 t}}$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \sum_{n=-\infty}^{\infty}{c_n e^{-j n \omega_0 t}}$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \sum_{n=-\infty}^{\infty}{\frac{1}{T} e^{-j n \omega_0 t}}$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \sum_{n=-\infty}^{\infty}{e^{-j n \omega_0 t}}$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \sum_{n=-\infty}^{\infty}{e^{-j n \frac{2\pi}{T} t}}$

Problema 2. Demostrar que

$\displaystyle \sum_{n=-\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} + \frac{2}{T} \sum_{1}^{\infty}{\cos{n \omega_0 t}}$

donde $\omega_0 = 2\pi/t$ .

Solución. Un tren periódico $\displaystyle \delta_T (t)$ de implusos unitarios se puede expresar como

$\displaystyle \large \delta_T (t) = \left\{ \begin{matrix} \sum_{n=- \infty}^{\infty}{\delta_T (t - nT)} & , & -T/2 < t < T/2 \\ \\ \delta (t) & , & -T/2 < t < T/2 \end{matrix} \right.$

Como el valor de $c_n$ es $1/T$ (ver Problema 1), lo anterior fue

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \sum_{n=-\infty}^{\infty}{e^{-j n \frac{2\pi}{T} t}}$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \sum_{n=-\infty}^{\infty}{e^{-j n \omega_0 t}}$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \left(\sum_{n=-\infty}^{-1}{e^{-j n \omega_0 t}} + e^{j0} + \sum_{n=1}^{\infty}{e^{-j n \omega_0 t}} \right)$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \left(\sum_{n=-\infty}^{-1}{e^{-j n \omega_0 t}} + 1 + \sum_{n=1}^{\infty}{e^{-j n \omega_0 t}} \right)$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \left(1 + \sum_{n=-\infty}^{-1}{e^{-j n \omega_0 t}} + \sum_{n=1}^{\infty}{e^{-j n \omega_0 t}} \right)$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \left[1 + \sum_{n=1}^{\infty}{\left(e^{j n \omega_0 t} + e^{-j n \omega_0 t}\right)} \right]$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \left[1 + \frac{2}{2} \sum_{n=1}^{\infty}{\left(e^{j n \omega_0 t} + e^{-j n \omega_0 t}\right)} \right]$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \left[1 + 2 \sum_{n=1}^{\infty}{\left(\frac{e^{j n \omega_0 t} + e^{-j n \omega_0 t}}{2} \right)} \right]$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \left(1 + 2 \sum_{n=1}^{\infty}{\cos{n \omega_0 t}} \right)$

$\displaystyle \therefore \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} + \frac{2}{T} \sum_{n=1}^{\infty}{\cos{n \omega_0 t}} = \frac{1}{T} + \frac{2}{T} \sum_{n=1}^{\infty}{\cos{\left(\frac{2 n \pi t}{T} \right)}}$

Y esto queda demostrado.

Problema 3. Hallar los coeficientes complejos de Fourier de la función $f(t)$ que se muestra en la figura 3.4.2.

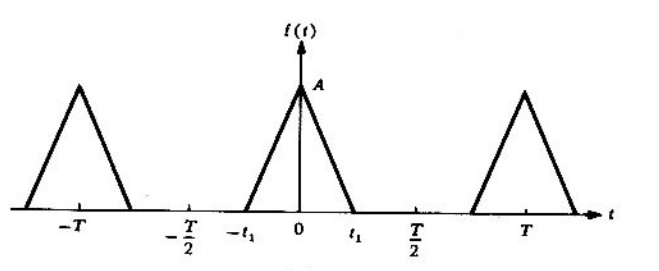
Figura 3.4.2 Función f(t) del problema 3. — *Figura 3.4.2 Función «f(t)» del problema 3.*

Solución. Suponiendo que

$\displaystyle f(t) = \sum_{n = -\infty}^{\infty}{c_n e^{jn \omega_0 t}}$

donde $\omega_0 = 2\pi/T$ . Diferenciando en ambos miembros

$\displaystyle \frac{d}{dt} [f(t)] = \frac{d}{dt} \left[\sum_{n = -\infty}^{\infty}{c_n e^{jn \omega_0 t}} \right]$

$\displaystyle f'(t) = \sum_{n = -\infty}^{\infty}{c_n (j n \omega_0) e^{jn \omega_0 t}}$

$\displaystyle f'(t) = \sum_{n = -\infty}^{\infty}{(j n \omega_0) c_n e^{jn \omega_0 t}}$

El resultado de la primera derivada se muestra en la figura 3.4.3.

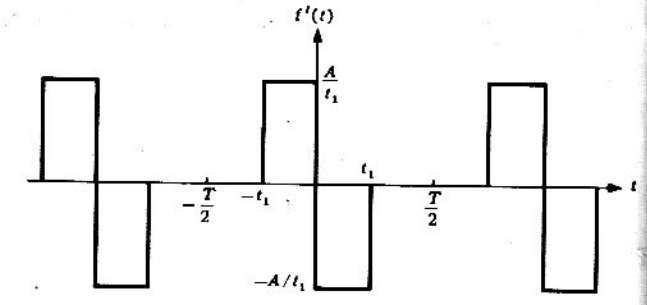
*Figura 3.4.3 Primera derivada de la función f(t) del problema 3.*

Diferenciando nuevamente en ambos miembros

$\displaystyle \frac{d}{dt} [f'(t)] = \frac{d}{dt} \left[\sum_{n = -\infty}^{\infty}{(j n \omega_0) c_n e^{jn \omega_0 t}} \right]$

$\displaystyle f''(t) = \sum_{n = -\infty}^{\infty}{(j n \omega_0) c_n (jn\omega_0) e^{jn \omega_0 t}}$

$\displaystyle f''(t) = \sum_{n = -\infty}^{\infty}{(j n \omega_0)^2 c_n e^{jn \omega_0 t}}$

El resultado de la segunda derivada se muestra en la figura 3.4.4.

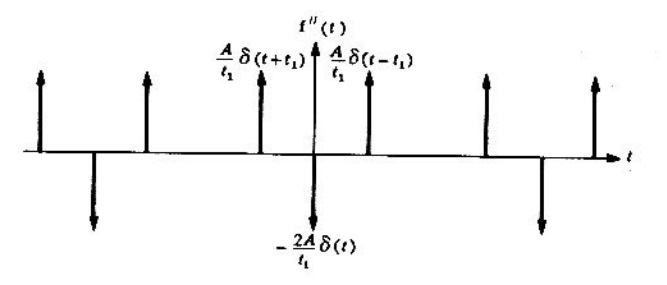
*Figura 3.4.4 Segunda derivada de la función f(t) del problema 3.*

Al igualar el resultado de $f''(t)$ con

$\displaystyle f''(t) = \sum_{n = - \infty}^{\infty}{\gamma_n e^{j n \omega_0 t}}$

Resulta lo siguiente

$\displaystyle f''(t) = \sum_{n = -\infty}^{\infty}{(j n \omega_0)^2 c_n e^{jn \omega_0 t}}$

$\displaystyle \sum_{n = - \infty}^{\infty}{\gamma_n e^{j n \omega_0 t}} = \sum_{n = -\infty}^{\infty}{(j n \omega_0)^2 c_n e^{jn \omega_0 t}}$

observando que

$\displaystyle \gamma_n = (j n \omega_0)^2 c_n$

De la figura 3.4.4, la segunda derivada de $f(t)$ en el intervalo $-T/2 < t < T/2$ es

$\displaystyle f''(t) = \frac{A}{t_1} \delta (t + t_1) - \frac{2A}{t_1} \delta (t) + \frac{A}{t_1} \delta (t - t_1)$

Por lo que, al determinar $\gamma_n$

$\displaystyle \gamma_n = \frac{1}{T} \int_{-T/2}^{T/2}{f''(t) e^{- j n \omega_0 t} \, dt}$

$\displaystyle \gamma_n = \frac{1}{T} \int_{-T/2}^{T/2}{\left[\frac{A}{t_1} \delta (t + t_1) - \frac{2A}{t_1} \delta (t) + \frac{A}{t_1} \delta (t - t_1) \right] e^{- j n \omega_0 t} \, dt}$

$\displaystyle \gamma_n = \frac{1}{T} \int_{-T/2}^{T/2}{\frac{A}{t_1} \delta (t + t_1) e^{- j n \omega_0 t} \, dt} - \frac{1}{T} \int_{-T/2}^{T/2}{\frac{2A}{t_1} \delta (t) e^{- j n \omega_0 t} \, dt} + \frac{1}{T} \int_{-T/2}^{T/2}{\frac{A}{t_1} \delta (t - t_1) e^{- j n \omega_0 t} \, dt}$

$\displaystyle \gamma_n = \frac{A}{t_1 T} \int_{-T/2}^{T/2}{\delta (t + t_1) e^{- j n \omega_0 t} \, dt} - \frac{2A}{t_1 T} \int_{-T/2}^{T/2}{\delta (t) e^{- j n \omega_0 t} \, dt} + \frac{A}{t_1 T} \int_{-T/2}^{T/2}{\delta (t - t_1) e^{- j n \omega_0 t} \, dt}$

$\displaystyle \gamma_n = \frac{A}{t_1 T} \cdot \left. e^{- j n \omega_0 t} \right|_{t = - t_1} - \frac{2A}{t_1 T} \cdot \left. e^{- j n \omega_0 t} \right|_{t = 0} + \frac{A}{t_1 T} \cdot \left. e^{- j n \omega_0 t} \right|_{t = t_1}$

$\displaystyle \gamma_n = \frac{A}{t_1 T} e^{- j n \omega_0 (- t_1)} - \frac{2A}{t_1 T} e^{- j n \omega_0 (0)} + \frac{A}{t_1 T} e^{- j n \omega_0 (t_1)}$

$\displaystyle \gamma_n = \frac{A}{t_1 T} e^{j n \omega_0 t_1} - \frac{2A}{t_1 T} (1) + \frac{A}{t_1 T} e^{- j n \omega_0 t_1}$

$\displaystyle \gamma_n = \frac{A}{t_1 T} e^{j n \omega_0 t_1} - \frac{2A}{t_1 T} + \frac{A}{t_1 T} e^{- j n \omega_0 t_1}$

$\displaystyle \gamma_n = \frac{2A}{2 t_1 T} e^{j n \omega_0 t_1} - \frac{2A}{t_1 T} + \frac{2A}{2 t_1 T} e^{- j n \omega_0 t_1}$

$\displaystyle \gamma_n = \frac{2A}{t_1 T} \left(\frac{1}{2} e^{j n \omega_0 t_1} - 1 + \frac{1}{2} e^{- j n \omega_0 t_1} \right)$

$\displaystyle \gamma_n = \frac{2A}{t_1 T} \left(\frac{1}{2} e^{j n \omega_0 t_1} + \frac{1}{2} e^{- j n \omega_0 t_1} - 1 \right)$

$\displaystyle \gamma_n = \frac{2A}{t_1 T} \left(\frac{e^{j n \omega_0 t_1} + e^{- j n \omega_0 t_1}}{2} - 1 \right)$

$\displaystyle \gamma_n = \frac{2A}{t_1 T} \left(\cos{n \omega_0 t_1} - 1 \right)$

$\displaystyle \gamma_n = \frac{2A}{t_1 T} \left(-1 + \cos{n \omega_0 t_1} \right)$

$\displaystyle \gamma_n = \frac{2A}{t_1 T} (-1) \left(1 - \cos{n \omega_0 t_1} \right)$

$\displaystyle \gamma_n = - \frac{2A}{t_1 T} \left(1 - \cos{n \omega_0 t_1} \right)$

$\displaystyle \gamma_n = - \frac{2A}{t_1 T} \cdot 2 \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2$

$\displaystyle \gamma_n = - \frac{4A}{t_1 T} \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2$

Luego, despejando $c_n$ de la ecuación $\gamma_n$

$\displaystyle \gamma_n = {(j n \omega_0)}^2 c_n$

$\displaystyle (j n \omega_0)^2 c_n = \gamma_n$

$\displaystyle c_n = \frac{\gamma_n}{(j n \omega_0)^2}$

Sustituyendo el valor de $\gamma_n$

$\displaystyle c_n = \frac{- \frac{4A}{t_1 T} \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2}{(j n \omega_0)^2}$

$\displaystyle c_n = - \frac{4A}{t_1 T} \cdot \frac{ \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2}{(j n \omega_0)^2}$

$\displaystyle c_n = - \frac{4A}{t_1 T} \cdot \frac{ \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2}{(j)^2 (n \omega_0)^2}$

$\displaystyle c_n = - \frac{4A}{t_1 T} \cdot \frac{ \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2}{(-1) (n \omega_0)^2}$

$\displaystyle c_n = \frac{4A}{t_1 T} \cdot \frac{ \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2}{(n \omega_0)^2}$

$\displaystyle c_n = \frac{4A}{t_1 T} \left(\frac{\sin{\frac{n \omega_0 t_1}{2}} }{n \omega_0} \right)^2$

$\displaystyle c_n = \frac{4A}{t_1 T} \left(\frac{\sin{\frac{n \omega_0 t_1}{2}} }{n \omega_0 \cdot \frac{2t_1}{2t_1}} \right)^2$

$\displaystyle c_n = \frac{4A}{t_1 T (\frac{2}{t_1})^2} \left(\frac{\sin{\frac{n \omega_0 t_1}{2}} }{\frac{n \omega_0 t_1}{2} }\right)^2$

$\displaystyle c_n = \frac{4A t_1^2}{4 t_1 T} \left(\frac{\sin{\frac{n \omega_0 t_1}{2}} }{\frac{n \omega_0 t_1}{2} }\right)^2$

$\displaystyle \therefore c_n = \frac{A t_1}{T} \left(\frac{\sin{\frac{n \omega_0 t_1}{2}} }{\frac{n \omega_0 t_1}{2} }\right)^2$

El valor de $c_0$ es

$\displaystyle c_0 = \frac{1}{T} \int_{-T/2}^{T/2}{f(t) \, dt}$

$\displaystyle c_0 = \frac{1}{T} \int_{-T/2}^{-t_1}{0 \, dt} + \frac{1}{T} \int_{-t_1}^{0}{\left(\frac{A}{t_1} t + A \right) \, dt} + \frac{1}{T} \int_{0}^{t_1}{\left(A - \frac{A}{t_1} t \right) \, dt} + \frac{1}{T} \int_{t_1}^{T/2}{0 \, dt}$

$\displaystyle c_0 = \frac{1}{T} \int_{-t_1}^{0}{\left(\frac{A}{t_1}t + A \right) \, dt} + \frac{1}{T} \int_{0}^{t_1}{\left(A - \frac{A}{t_1} t \right) \, dt}$

$\displaystyle c_0 = \frac{A}{t_1 T} \int_{-t_1}^{0}{t \, dt}+ \frac{A}{T} \int_{-t_1}^{0}{dt} + \frac{A}{T} \int_{0}^{t_1}{dt} - \frac{A}{t_1 T} \int_{0}^{t_1}{t \, dt}$

$\displaystyle c_0 = \frac{A}{t_1 T} \int_{-t_1}^{0}{t \, dt}+ \frac{A}{T} \int_{-t_1}^{t_1}{dt} - \frac{A}{t_1 T} \int_{0}^{t_1}{t \, dt}$

$\displaystyle c_0 = \frac{A}{t_1 T} \left[\frac{1}{2} t^2 + C \right]_{-t_1}^{0} + \frac{A}{T} \left[ t + C \right]_{-t_1}^{t_1} - \frac{A}{t_1 T} \left[\frac{1}{2} t^2 + C \right]_{0}^{t_1}$

$\displaystyle c_0 = \frac{A}{t_1 T} \left[\frac{1}{2} (0) - \frac{1}{2} t^2_1 \right] + \frac{A}{T} \left[ t_1 - (-t_1) \right] - \frac{A}{t_1 T} \left[\frac{1}{2} t_1^2 - \frac{1}{2} (0)^2 \right]$

$\displaystyle c_0 = \frac{A}{t_1 T} \left(- \frac{1}{2} t^2_1 \right) + \frac{A}{T} \left( 2 t_1 \right) - \frac{A}{t_1 T} \left(\frac{1}{2} t_1^2 \right)$

$\displaystyle c_0 = - \frac{At_1}{2T} + \frac{2At_1}{T} - \frac{At_1}{2T}$

$\displaystyle \therefore c_0 = \frac{At_1}{T}$

Como se esperaba.

Problema 4. Hallar los coeficientes complejos de Fourier de la función $f(t)$ que se muestra en la figura 3.4.5, mediante la serie compleja de Fourier de un tren periódico de impulsos unitarios.

Solución. Suponiendo que

$\displaystyle f(t) = \sum_{n = -\infty}^{\infty}{c_n e^{jn \omega_0 t}}$

donde $\omega_0 = 2\pi/T$ . Diferenciando en ambos miembros

$\displaystyle \frac{d}{dt} [f(t)] = \frac{d}{dt} \left[\sum_{n = -\infty}^{\infty}{c_n e^{jn \omega_0 t}} \right]$

$\displaystyle f'(t) = \sum_{n = -\infty}^{\infty}{c_n (j n \omega_0) e^{jn \omega_0 t}}$

$\displaystyle f'(t) = \sum_{n = -\infty}^{\infty}{(j n \omega_0) c_n e^{jn \omega_0 t}}$

El resultado de la primera derivada se muestra en la figura 3.4.6.

Diferenciando nuevamente en ambos miembros

$\displaystyle \frac{d}{dt} [f'(t)] = \frac{d}{dt} \left[\sum_{n = -\infty}^{\infty}{(j n \omega_0) c_n e^{jn \omega_0 t}} \right]$

$\displaystyle f''(t) = \sum_{n = -\infty}^{\infty}{(j n \omega_0) c_n (jn\omega_0) e^{jn \omega_0 t}}$

$\displaystyle f''(t) = \sum_{n = -\infty}^{\infty}{(j n \omega_0)^2 c_n e^{jn \omega_0 t}}$

El resultado de la segunda derivada se muestra en la figura 3.4.7.

De la figura 3.4.7, la segunda derivada de $f(t)$ en el intervalo $-\infty < t < \infty$ es

$\displaystyle f''(t) = \frac{A}{t_1} \sum_{n = -\infty}^{\infty}{\delta (t + t_1 - nT)} - \frac{2A}{t_1} \sum_{n = -\infty}^{\infty}{\delta (t - nT)} + \frac{A}{t_1} \sum_{n=-\infty}^{\infty}{\delta (t - t_1 - nT)}$

Después, la serie compleja de Fourier de un tren periódico de impulsos unitarios es

\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - nT)} = \frac{1}{T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 t}}

donde $\omega_0 = 2\pi/T$ . De la ecuación (1), agregando $t_1$ dentro de cada función delta, resulta

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t + t_1 - nT)} = \frac{1}{T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 (t + t_1)}}$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t + t_1 - nT)} = \frac{1}{T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 t}e^{jn\omega_0 t_1}}$

De la ecuación (1), agregando $- t_1$ dentro de cada función delta, resulta

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - t_1 - nT)} = \frac{1}{T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 (t - t_1)}}$

$\displaystyle \sum_{n = -\infty}^{\infty}{\delta (t - t_1 - nT)} = \frac{1}{T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 t}e^{-jn\omega_0 t_1}}$

Reemplazando estos dos últimos resultados y la ecuación (1) con la función $f''(t)$

$\displaystyle f''(t) = \frac{A}{t_1} \cdot \frac{1}{T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 t}e^{jn\omega_0 t_1}} - \frac{2A}{t_1} \cdot \frac{1}{T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 t}} + \frac{A}{t_1} \cdot\frac{1}{T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 t}e^{-jn\omega_0 t_1}}$

$\displaystyle f''(t) = \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 t}e^{jn\omega_0 t_1}} - \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{2e^{jn\omega_0 t}} + \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{e^{jn\omega_0 t}e^{-jn\omega_0 t_1}}$

$\displaystyle f''(t) = \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{(e^{jn\omega_0 t}e^{jn\omega_0 t_1} - 2e^{jn\omega_0 t} + e^{jn\omega_0 t}e^{-jn\omega_0 t_1})}$

$\displaystyle f''(t) = \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{(e^{jn\omega_0 t_1} - 2 + e^{-jn\omega_0 t_1}) e^{jn\omega_0 t}}$

$\displaystyle f''(t) = \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{(e^{jn\omega_0 t_1} + e^{-jn\omega_0 t_1} - 2) e^{jn\omega_0 t}}$

$\displaystyle f''(t) = \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{\left[\frac{2}{2} (e^{jn\omega_0 t_1} + e^{-jn\omega_0 t_1}) - 2 \right] e^{jn\omega_0 t}}$

$\displaystyle f''(t) = \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{\left[2 \cdot \left( \frac{e^{jn\omega_0 t_1} + e^{-jn\omega_0 t_1}}{2} \right) - 2 \right] e^{jn\omega_0 t}}$

$\displaystyle f''(t) = \frac{A}{t_1 T} \sum_{n = -\infty}^{\infty}{\left(2 \cos{n \omega_0 t_1} - 2 \right) e^{jn\omega_0 t}}$

$\displaystyle f''(t) = \frac{2A}{t_1 T} \sum_{n = -\infty}^{\infty}{\left( \cos{n \omega_0 t_1} - 1 \right) e^{jn\omega_0 t}}$

$\displaystyle f''(t) = - \frac{2A}{t_1 T} \sum_{n = -\infty}^{\infty}{\left(1 - \cos{n \omega_0 t_1} \right) e^{jn\omega_0 t}}$

$\displaystyle f''(t) = - \frac{2A}{t_1 T} \sum_{n = -\infty}^{\infty}{2 \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2 e^{jn\omega_0 t}}$

$\displaystyle f''(t) = \sum_{n = -\infty}^{\infty}{\left( - \frac{4A}{t_1 T} \right) \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2 e^{jn\omega_0 t}}$

Al igualar el resultado de $f''(t)$ con

$\displaystyle f''(t) = \sum_{n = -\infty}^{\infty}{(j n \omega_0)^2 c_n e^{jn \omega_0 t}}$

(obtenido del problema 3) resulta lo siguiente

$\displaystyle \sum_{n = -\infty}^{\infty}{\left( - \frac{4A}{t_1 T} \right) \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2 e^{jn\omega_0 t}} = \sum_{n = -\infty}^{\infty}{(j n \omega_0)^2 c_n e^{jn \omega_0 t}}$

Por lo que

$\displaystyle \left( - \frac{4A}{t_1 T} \right) \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2 = (j n \omega_0)^2 c_n$

$\displaystyle (j n \omega_0)^2 c_n = \left( - \frac{4A}{t_1 T} \right) \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2$

$\displaystyle - n^2 \omega_0^2 c_n = - \frac{4A}{t_1 T} \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2$

$\displaystyle c_n = \frac{4A}{t_1 T n^2 \omega_0^2} \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2$

$\displaystyle c_n = \frac{4A}{t_1 T n^2 \omega_0^2 \cdot \frac{2^2 t_1^2}{2^2 t_1^2}} \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2$

$\displaystyle c_n = \frac{4A}{t_1 T \cdot \frac{2^2}{t_1^2} \cdot \frac{n^2 \omega_0^2 t_1^2}{2^2}} \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2$

$\displaystyle c_n = \frac{4At_1^2}{t_1 T \cdot 4 \cdot \left(\frac{n \omega_0 t_1}{2}\right)^2} \left(\sin{\frac{n \omega_0 t_1}{2}} \right)^2$

$\displaystyle \therefore c_n = \frac{At_1}{T} \left(\frac{\sin{\frac{n \omega_0 t_1}{2}}}{\frac{n \omega_0 t_1}{2}} \right)^2$

Y el valor de $c_0$ es

$\displaystyle \therefore c_0 = \frac{At_1}{T}$

Evaluación de los coeficientes complejos de Fourier por medio de la función δ. Fourier.

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Evaluación de los coeficientes complejos de Fourier por medio de la función δ. Fourier.

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta