Circuitos magnéticos. Problema 2. Máquinas eléctricas.

Problema 3. En la figura 1.1.3 muestra un núleo ferromagnético cuya permeabilidad relativa es de 1500. Las demás dimensiones del núcleo se pueden ver en el diagrama. La profundidad del núcleo es de 5 cm. Los entrehierros de las partes izquierda y derecha del núcleo tiene 0.050 cm y 0.070 cm, respectivamente. Debido a los efectos marginales, el área efectiva de los entrehierros se incrementa 5% respecto del área física. Si hay una bobina de 300 vueltas enrollada en la columna central del núcleo y por ella pasa una corriente de 1.0 A, ¿cuál es el flujo en las columnas izquierda, cental y derecha del núcleo? ¿Cuál es la densidad de flujo de cada entrehierro?

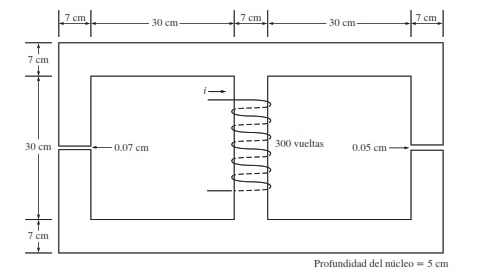
Figura P1.3 Núcleo ferromagnético del problema 3. — *Figura 1.1.3 Núcleo ferromagnético del problema 3.*

Solución. Tomando los datos del problema, se tiene que $\mu_r = 1500$ , profundidad del núcleo = 5 cm = 0.05 m y $N=500$ espiras.

Analizando el núcleo ferromagnético, se tienen las siguientes medidas asignadas:

Columna central del núcleo

$l_1 = 3.5 + 30 + 3.5 = 37 \ cm = 0.37 \ m$

Columna izquierda del núcleo

$l_2 = 3.5 + 30 + 3.5 + 3.5 + 30 + 3.5 + 3.5 + 30 + 3.5 = 111 \ cm = 1.11 \ m$

Entrehierro izquierdo del núcleo

$l_3 = 0.07 \ cm = 0.0007 \ m$

Columna derecha del núcleo

$l_4 = 3.5 + 30 + 3.5 + 3.5 + 30 + 3.5 + 3.5 + 30 + 3.5 = 111 \ cm = 1.11 \ m$

Entrehierro derecho del núcleo

$l_5 = 0.07 \ cm = 0.0007 \ m$

Ahora, determinando las áreas de cada sección del núcleo, resulta:

Sección transversal de la columna central

$A_1 = (0.07 \ m)(0.05 \ m) = 0.0035 \ m^2$

Sección transversal de la columna izquierda

$A_2 = (0.07 \ m)(0.05 \ m) = 0.0035 \ m^2$

Sección transversal del entrehierro izquierdo

$A_3 = (0.07 \ m)(0.05 \ m)(1.05) = 0.0037 \ m^2$

Sección transversal de la columna derecha

$A_4 = (0.07 \ m)(0.05 \ m) = 0.0035 \ m^2$

Sección transversal del entrehierro derecha

$A_5 = (0.07 \ m)(0.05 \ m)(1.05) = 0.0037 \ m^2$

Cálculo de las reluctancias de cada columna y entrehierro.

Columna central del núcleo

$\displaystyle \mathcal{R}_1 = \frac{l_1}{\mu \ A_1} = \frac{l_1}{\mu_r \mu_0 \ A_1}$

$\displaystyle \mathcal{R}_1 = \frac{0.37 \ m}{(1500)(4\pi \times 10^{-7} \ H/m)(0.0035 \ m^2)} = 56,083.04 \ A \cdot espiras / Wb$

$\mathcal{R}_1 = 56.08 \ (kA \cdot espiras / Wb)$

Columna izquierda del núcleo

$\displaystyle \mathcal{R}_2 = \frac{l_2}{\mu \ A_2} = \frac{l_2}{\mu_r \mu_0 \ A_2}$

$\displaystyle \mathcal{R}_2 = \frac{1.11 \ m}{(1500)(4\pi \times 10^{-7} \ H/m)(0.0035 \ m^2)} = 168,249 \ A \cdot espiras / Wb$

$\mathcal{R}_2 = 168.25 \ (kA \cdot espiras / Wb)$

Entrehierro de la columna izquierda del núcleo

$\displaystyle \mathcal{R}_3 = \frac{l_3}{\mu_0 \ A_3}$

$\displaystyle \mathcal{R}_3 = \frac{0.0007 \ m}{(4\pi \times 10^{-7} \ H/m)(0.0037 \ m^2)} = 150,551.62 \ A \cdot espiras / Wb$

$\mathcal{R}_3 = 150.55 \ (kA \cdot espiras / Wb)$

Columna derecha del núcleo

$\displaystyle \mathcal{R}_4 = \frac{l_4}{\mu \ A_4} = \frac{l_4}{\mu_0 \mu_r \ A_3}$

$\displaystyle \mathcal{R}_4 = \frac{1.11 \ m}{(1500)(4\pi \times 10^{-7} \ H/m)(0.0035 \ m^2)} = 168,249.12 \ A \cdot espiras / Wb$

$\mathcal{R}_4 = 168.25 \ (kA \cdot espiras / Wb)$

Entrehierro de la columna derecha del núcleo

$\displaystyle \mathcal{R}_5 = \frac{l_5}{\mu_0 \ A_5}$

$\displaystyle \mathcal{R}_5 = \frac{0.0005 \ m}{(4\pi \times 10^{-7} \ H/m)(0.0037 \ m^2)} = 107,536.87 \ A \cdot espiras / Wb$

$\mathcal{R}_5 = 107.54 \ (kA \cdot espiras / Wb)$

Para determinar la reluctancia total, el análisis del núcleo con sus respectivas longitudes asignadas, se tiene lo siguiente:

$\displaystyle \mathcal{R}_T = \mathcal{R}_1 + \frac{1}{\frac{1}{\mathcal{R}_2 + \mathcal{R}_3} + \frac{1}{\mathcal{R}_4 + \mathcal{R}_5}} = \mathcal{R}_1 + \frac{(\mathcal{R}_2 + \mathcal{R}_3)(\mathcal{R}_4 + \mathcal{R}_5)}{\mathcal{R}_2 + \mathcal{R}_3 + \mathcal{R}_4 + \mathcal{R}_5}$

$\displaystyle \mathcal{R}_T = 56.08 + \frac{(168.25 + 150.55)(168.25 + 107.54)}{168.25 + 150.55 + 168.25 + 107.54}$

$\mathcal{R}_T = 203.96 \ (kA \cdot espiras/ Wb)$

Cálculo del flujo total del núcleo.

$\mathcal{F} = \phi \ \mathcal{R}$

$\displaystyle \phi = \frac{\mathcal{F}}{\mathcal{R}} = \frac{N \ i}{\mathcal{R}}$

$\displaystyle \phi = \frac{(300 \ espiras)(1 \ A)}{203.96 \times 10^3 A\ espiras / Wb}$

$\phi = 1.47 \times 10^{-3} Wb = 1.47 \ mWb$

El flujo central es

$\phi_{central} = \phi$

$\mathbf{\phi_{central} = 1.47 \ mWb}$

El flujo de la columna izquierda es

$\displaystyle \phi_{izq} = \phi \ \left( \frac{\mathcal{R}_4 + \mathcal{R}_5}{\mathcal{R}_2 + \mathcal{R}_3 + \mathcal{R}_4 + \mathcal{R}_5} \right)$

$\displaystyle \phi_{izq} = (1.47 \times 10^{-3}) \ \left(\frac{168.25 + 107.54}{168.25 + 150.55 + 168.25 + 107.54} \right)$

$\mathbf{\phi_{izq} = 0.68 \times 10^{-3} \ Wb = 0.68 \ mWb}$

El flujo de la columna derecha es

$\displaystyle \phi_{der} = \phi \ \left( \frac{\mathcal{R}_2 + \mathcal{R}_3}{\mathcal{R}_2 + \mathcal{R}_3 + \mathcal{R}_4 + \mathcal{R}_5} \right)$

$\displaystyle \phi_{der} = (1.47 \times 10^{-3}) \ \left(\frac{168.25 + 150.55}{168.25 + 150.55 + 168.25 + 107.54} \right)$

$\mathbf{\phi_{der} = 0.79 \times 10^{-3} \ Wb = 0.79 \ mWb}$

Cálculo de la densidad de flujo del entrehierro izquierdo

$\phi_{izq} = B_{izq} \ A_3$

$\displaystyle B_{izq} = \frac{\phi_{izq}}{A_3}$

$\displaystyle B_{izq} = \frac{0.68 \times 10^{-3} \ Wb}{0.0037 \ m^2}$

$\mathbf{B_{izq} = 0.184 \ T}$

Cálculo de la densidad de flujo del entrehierro derecho

$\phi_{der} = B_{der} \ A_5$

$\displaystyle B_{der} = \frac{\phi_{der}}{A_5}$

$\displaystyle B_{der} = \frac{0.79 \times 10^{-3} \ Wb}{0.0037 \ m^2}$

$\mathbf{B_{der} = 0.214 \ T}$

8 comentarios sobre “Circuitos magnéticos. Problema 2. Máquinas eléctricas.”

Jacob Ruiz dice:

13 agosto, 2020 a las 8:42 am

Me podria aclarar de donde sale la expresión de la reluctancia total?

Me gustaMe gusta

Responder
Cesar Augusto dice:

24 agosto, 2020 a las 2:59 pm

Hola Jacob. Te comento que la reluctancia total se obtiene a partir de un conjunto de reluctancias similares a las resistencias en serie y en paralelo; recuerda que cada reluctancia fue obtenida en cada columna y la FMM es como la fuente de voltaje. Saludos…

Me gustaMe gusta

Responder
Miguel Angel dice:

26 agosto, 2020 a las 11:38 am

Hola me podrías explicar como sacaste la sección transversal del entrehierro

Me gustaMe gusta

Responder
JUAN CAMILO JIMENEZ LOPEZ dice:

30 noviembre, 2020 a las 4:06 pm

hola, por que en la densidad de flujo en el entrehierro no utiliza el área del entrehierro?

Me gustaMe gusta

Responder
1. Cesar Augusto dice:
  
  30 noviembre, 2020 a las 6:41 pm
  
  Hola Juan. Lo siento, había considerado el proceso de tomar en cuenta los lados 7 cm y 5 cm pero no el efecto marginal. Ya está corregido ese detalle. Se te agradece mucho. Saludos…
  
  Me gustaMe gusta
  
  Responder
Karla May dice:

10 abril, 2021 a las 11:56 pm

Hola, disculpa de donde sale el 1.05 del área del entrehierro?

Me gustaMe gusta

Responder
ZAPATA SANTILLAN JESUS ANGEL dice:

30 septiembre, 2021 a las 5:20 pm

de donde salió el 1.05 de la sección transversal del hierro izquierdo

Me gustaMe gusta

Responder
1. Cesar Reyes dice:
  
  30 septiembre, 2021 a las 10:59 pm
  
  Hola Jesús. El enunciado del problema menciona «Debido a los efectos marginales, el área efectiva de los entrehierros se incrementa 5% respecto del área física» eso significa que del 100% del área al haber un incremento del 5% esto conlleva a un total del 105%, que al realizar los cálculos correspondientes, el valor toma 1.05.
  
  Me gustaMe gusta
  
  Responder