Transformadores. Problema 2. Máquinas eléctricas.

Problema 2. En la figura 2.2.1 se muestra un sistema de potencia monofásico. La fuente de potencia alimenta a un transformador de 100 (kVA) y 14/24 (kV) a través de un alimentador con una impedancia de 38.2 + j140 (Ω). La impedancia en serie equivalente del transformador referida a su lado de bajo voltaje es 0.10 + j0.40 (Ω). La carga en el transformador es de 90 (kW) con un F.P. = 0.80 en retraso y 2300 (V).

Figura 2.2.1 Sistema de potencia monofásico.

a) ¿Cuál es el voltaje en la fuente de potencia del sistema?

b) ¿Cuál es la regulación de voltaje del transformador?

c) En general, ¿qué tan eficiente es el sistema de potencia?

Solución. El sistema de potencia monofásico se puede representar mediante un circuito equivalente, como se muestra a continuación

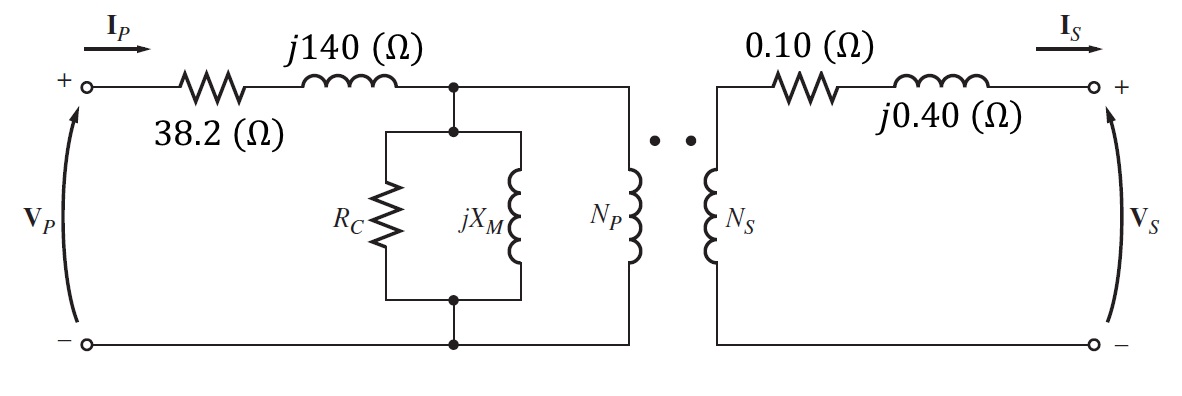
Figura 2.2.2 Circuito eléctrico del sistema de potencia monofasico

Para poder resolver este problema, el circuito se puede referir al lado de bajo voltaje (lado secundario). Así que los datos que en algunos se toman directamente y otros se han calculado son:

Relación de vueltas del transformador

$\displaystyle a = \frac{14 \ (kV)}{2.4 \ (kV)} = \frac{14 \times 10^3 (V)}{2.4 \times 10^3 (V)} = 5.833$

Impedancia del alimentador

$\displaystyle \frac{R_P}{a^2} = \frac{38.2}{(5.833)^2} = 1.123 \ (\Omega)$

$\displaystyle \frac{X_P}{a^2} = \frac{140}{(5.833)^2} = 4.115 \ (\Omega)$

$\displaystyle \frac{Z_{linea}}{a^2} = \frac{R_P}{a^2} + j\frac{X_P}{a^2} = 1.1.23 + j4.115 \ (\Omega)$

Impedancia en serie

$Z_{SE} = 0.10 + j0.40 \ (\Omega)$

Factor de potencia

$F.P. = \cos{\theta} = 0.80$

Ángulo θ

$\theta = \arccos{(0.80)} = 36.87$ °

Corriente en el lado secundario

$P_S = V_S I_S \cos{\theta}$

$\displaystyle I_S = \frac{P_S}{V_S \cos{\theta}}$

$\displaystyle I_S = \frac{90 \ (kW)}{(2300 \ V)(0.80)} = \frac{90 \times 10^3 (W)}{(2300 \ V)(0.80)}$

$\displaystyle I_S = 48.913 \ (A)$

Fasor de la corriente en el lado secundario

$\boldsymbol{I_S} = I_S \angle -\theta = 48.913 \angle - 36.87$ °

Fasor del voltaje en el lado secundario

$\displaystyle \boldsymbol{V_S} = 2300 \angle 0$ °

Todos estos datos se han plasmado en la siguiente figura.

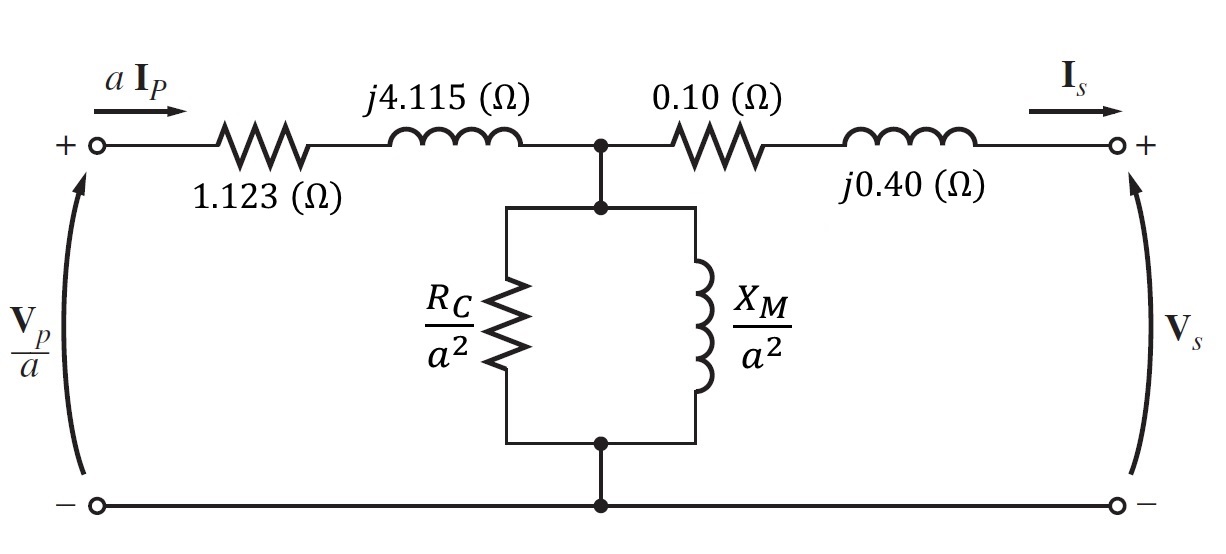
Figura 2.2.3 Modelo del sistema para el transformador referido al lado de bajo voltaje (lado secundario).

Como no hay datos en la rama de excitación, ésta se puede ignorar teniendo un nuevo circuito.

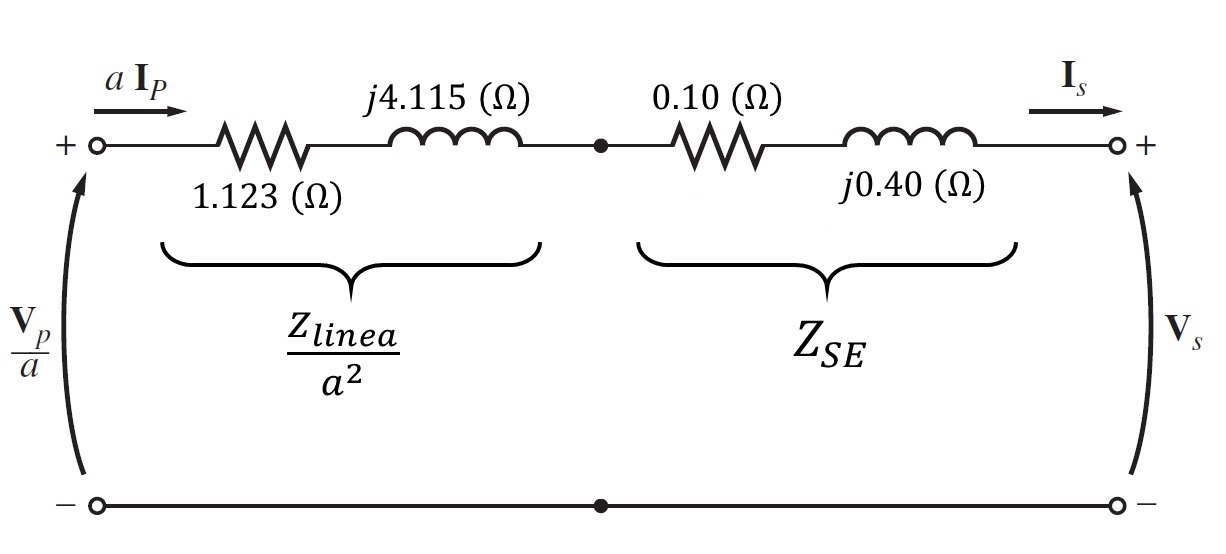
Figura 2.2.4 Modelo del sistema para el transformador referido al lado de bajo voltaje sin rama de excitación.

Tomando la figura 2.2.4, la fórmula para calcular el voltaje de la fuente (voltaje primario) de potencia de este sistema (referido al lado secundario) es

$\displaystyle \frac{\boldsymbol{V_P}}{a} = \boldsymbol{V_S} + \frac{Z_{linea}}{a^2} \cdot \boldsymbol{I_S} + Z_{SE} \cdot \boldsymbol{I_S}$

Sustituyendo los datos calculados

$\displaystyle \frac{\boldsymbol{V_P}}{a} = 2300 \angle 0 + (1.123 + j4.115)(48.913 \angle -36.87) + (0.10 + j0.40)(48.913 \angle -36.87)$

$\displaystyle \frac{\boldsymbol{V_P}}{a} = 2300 \angle 0 + (4.265 \angle 74.74)(48.913 \angle -36.87) + (0.412 \angle 75.96)(48.913 \angle -36.87)$

$\displaystyle \frac{\boldsymbol{V_P}}{a} = 2300 \angle 0 + 208.614 \angle 37.87 + 20.152 \angle 39.09$

$\displaystyle \frac{\boldsymbol{V_P}}{a} = 2300 + j0 + 164.681 + j128.062 + 15.641 + j12.707 = 2480.322 + j140.769$

$\displaystyle \frac{\boldsymbol{V_P}}{a} = 2484.313 \angle 3.25$ ° (V)

Despejando la variable $\boldsymbol{V_P}$ , se tiene el siguiente resultado

$\displaystyle \boldsymbol{V_P} = a \cdot (2482.313 \angle 3.25)$

$\displaystyle \boldsymbol{V_P} = (5.833) \cdot (2482.313 \angle 3.25)$

$\displaystyle \boldsymbol{V_P} = 14479.332 \angle 3.25 (V)$

Por lo tanto,

$\displaystyle \therefore \boldsymbol{V_{fuente}} = \boldsymbol{V_P} = 14479.332 \angle 3.25 (V) \approx 14.5 \angle 3.25 \ (kV)$

Solución b). Para determinar la regulación de voltaje del transformador, primero se debe calcular el voltaje que pertenece al devanado primario (ya referido al lado secundario) tomando como base la figura 2.2.4.

$\displaystyle \frac{\boldsymbol{V_P}}{a} = \boldsymbol{V_S} + \boldsymbol{I_S} \cdot Z_{SE}$

$\displaystyle \frac{\boldsymbol{V_P}}{a} = 2300 \angle 0 + (48.913 \angle -36.87)(0.10 + j0.40) = 2300 \angle 0 + (48.913 \angle -36.87)(0.412 \angle 75.96)$

$\displaystyle \frac{\boldsymbol{V_P}}{a} = 2300 \angle 0 + 20.152 \angle 39.09 = 2300 + j0 = 15.641 + j12.707= 2315.641 + j12.707$

$\displaystyle \frac{\boldsymbol{V_P}}{a} = 2315.676 \angle 0.31$

Calculando la regulación de voltaje,

$\displaystyle RV = \frac{\frac{V_P}{a} - V_S}{V_S} \times 100$ %

$\displaystyle RV = \frac{2315.676 - 2300}{2300} \times 100$ %

$\therefore RV = 0.682$ %

Solución c). En general, la eficiencia del sistema de potencia será la razón desde la potencia de salida hasta la potencia de entrada. La potencia de salida es 90 (kW) y la potencia de entrada es

$\displaystyle P_{ent} = \left( \frac{V_P}{a} \right) I_S \cos{\theta}$

$\displaystyle P_{ent} = (2484.313)(48.913) \cos{(36.87+3.25)}$

$\displaystyle P_{ent} = 92922.25 \ W = 92.92 \ (kW)$

Por tanto, la eficiencia del sistema de potencia es

$\displaystyle \eta = \frac{P_{sal}}{P_{ent}} \times 100$

$\displaystyle \eta = \frac{90 \ kW}{92.92} \times 100$ %

$\therefore \eta = 96.86$ %

8 comentarios sobre “Transformadores. Problema 2. Máquinas eléctricas.”

Jesus dice:

19 enero, 2021 a las 11:44 pm

Cordiales saludos amigo, le agradezco su gran colaboracion a todos nosotros los estudiantes de ingenieria, su aporte me ha sacado de una gran duda, espero siga motivado a seguir compartiendo sus conocimientos con nosotros, le deseo salud a usted y a toda su familia. Saludos desde Mexico

Me gustaMe gusta

Responder
1. Cesar Augusto dice:
  
  20 enero, 2021 a las 7:48 am
  
  Muchas gracias Jesus. Claro que es un placer seguir compartiendo más información. Después de todo, es para todos.
  
  Me gustaMe gusta
  
  Responder
MANUEL RINCON GONZALEZ dice:

21 marzo, 2021 a las 12:13 am

una pregunta cuando dices «Como no hay datos en la rama de excitación, ésta se puede ignorar teniendo un nuevo circuito.»¿ te refieres a la rama superior donde se encuentra la impedancia 38.2 + j140 (Ω)?,y si es asi por que se remplaza por el valor de Impedancia del alimentador?

Me gustaMe gusta

Responder
1. Cesar Reyes dice:
  
  21 marzo, 2021 a las 8:02 pm
  
  Hola Manuel. No significa que se haya reemplazado los valores de la rama de excitacion por los de la impedancia del lado primario. Más bien, al no haber datos en la rama de excitación (Rc y Xm), estos no se toman en cuenta. Durante esta solución, se observa que utiliza solo Rp, Xp, Rs y Xs (dependiendo del lado que se esté referido en el transformador) y no se considera primordial los de la rama de excitación para obtener corriente, voltaje, potencia a menos que el problema lo haya mencionado. Lo que si es importante son los valores de Rp, Xp, Rs y Xs y que lado se esté referido el transformador (lo que describa el problema); los valores de Rc y Xm solo te pueden servir para representarlos en un circuito o diagrama y conocer sus valores. Saludos…
  
  Me gustaMe gusta
  
  Responder
julio dice:

11 abril, 2021 a las 9:19 pm

cuando despejaste vp, porque la a no estaba ala cuadrado

Me gustaMe gusta

Responder
1. Cesar Reyes dice:
  
  11 abril, 2021 a las 9:32 pm
  
  Hola Julio, gracias por la observación. En realidad la redacción debe ser V_P / a. Saludos…
  
  Me gustaMe gusta
  
  Responder
henry lopez dice:

8 septiembre, 2021 a las 2:48 pm

si nos dan valor de impedancia como lo podemos hacer como lo remplazamos le agradezco la ayuda

Me gustaMe gusta

Responder
1. henry lopez dice:
  
  8 septiembre, 2021 a las 2:49 pm
  
  perdon no de impedancia sino de excitacion
  
  Me gustaMe gusta
  
  Responder