Aplicaciones de las ecuaciones de primer grado y grado superior. Ecuaciones diferenciales.

Problemas resueltos.

Problema 1. Hallar la curva para la que:

a) La suma de los segmentos interceptados por la recta tangente en los ejes coordenados es igual a $k$ .

b) El producto de los segmentos interceptados por la recta tangente en los ejes coordenados es igual a $k$ .

c) La porción de recta tangente interceptada por los ejes coordenados es de longitud constante $k$ .

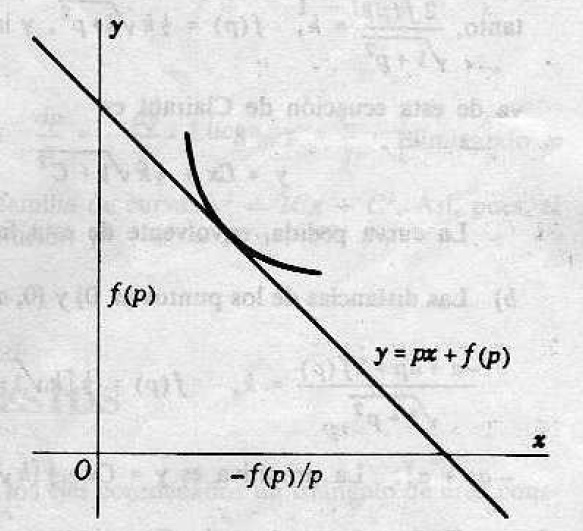
Solución. Sea la ecuación diferencial que representa la ecuación de la recta tangente

$y = px + f(p)$

donde los segmentos interceptados en el eje $x$ y en el eje $y$ son $-f(p)/p$ y $f(p)$ , la cual tiene la forma de la ecuación de Clairaut; esto se puede representar en la siguiente figura

Solución a). Según del enunciado del inciso a)

$\displaystyle f(p) - \frac{f(p)}{p} = k$

Despejando $f(p)$ resulta que

$\displaystyle \left(1 - \frac{1}{p} \right) f(p) = k$

$\displaystyle \left(\frac{p -1}{p} \right) f(p) = k$

$\displaystyle f(p) = \frac{kp}{(p-1)}$

$\displaystyle f(p) = - \frac{kp}{(1-p)}$

Tomando la ecuación de la recta tangente

$\displaystyle y = px + f(p)$

$\displaystyle y = px - \frac{kp}{(1-p)}$

Entonces, su primitiva es

$\displaystyle y = Cx - \frac{Ck}{(1-C)}$

Es decir

$\displaystyle y - Cx + \frac{Ck}{(1-C)} = 0$

$(1-C)(y - Cx) + Ck = 0$

$y - Cx - Cy + C^2 x + Ck = 0$

$C^2 x - C(x+y-k) + y = 0$

La curva pedida, envolvente de la familia, se determina de la siguiente manera (hallando el discriminante)

$\displaystyle b^2 -4ac =0$

$(x+y-k)^2 - 4(x)(y) = 0$

$(x+y-k)^2 - 4xy = 0$

$(x+y-k)^2 = 4xy$

Es decir,

$\displaystyle x^{1/2} \pm y^{1/2} = k^{1/2}$

Se observa que esta curva es una envolvente (solución singular) ya que satisface la ecuación diferencial y no se puede obtener de la primitiva y no se puede obtener de la primitiva dando un valor a C.

Solución b). Según el enunciado del inciso b)

$\displaystyle f(p) \left[- \frac{f(p)}{p} \right] = k$

Despejando $f(p)$ , resulta que

$\displaystyle - \frac{[f(p)]^2}{p} = k$

$\displaystyle [f(p)]^2 = -kp$

$\displaystyle f(p) = \pm \sqrt{-kp}$

Sustituyendo en la ecuación de la recta tangente

$\displaystyle y = xp \pm \sqrt{-kp}$

Por lo que su primitiva es

$\displaystyle y = Cx \pm \sqrt{-Ck}$

o también

$x^2 C^2 + (k-2xy) C + y^2 = 0$

La curva pedida, envolvente de la familia, se determina de la siguiente manera (hallando el discriminante)

$\displaystyle b^2 - 4ac = 0$

$(k-2xy)^2 - 4(x^2)(y^2) = 0$

$k^2 - 4kxy + 4x^2 y^2- 4x^2 y^2 = 0$

$4xy = k$

Solución c). Según del enunciado del inciso c)

$\displaystyle \sqrt{[f(p)]^2 + \left[\frac{f(p)}{p} \right]^2} = k$

Despejando $f(p)$

$\displaystyle [f(p)]^2 + \left[\frac{f(p)}{p} \right]^2 = k^2$

$\displaystyle [f(p)]^2 (1 + \frac{1}{p^2}) = k^2$

$\displaystyle [f(p)]^2 (\frac{p^2 + 1}{p^2}) = k^2$

$\displaystyle [f(p)]^2 = \frac{k^2 p^2}{(p^2 + 1)}$

$\displaystyle f(p) = \pm \sqrt{\frac{k^2 p^2}{(p^2 + 1)}}$

$\displaystyle f(p) = \pm \frac{k p}{\sqrt{p^2 + 1}}$

Sustituyendo en la ecuación de la recta tangente

$\displaystyle y = xp \pm \frac{k p}{\sqrt{p^2+1}}$

Y su primitiva es

$\displaystyle y = Cx \pm \frac{C k}{\sqrt{C^2+1}}$

Para determinar su ecuación envolvente, primero se deriva este último resultado con respecto a $C$ .

$\displaystyle 0 = x \pm \frac{k}{(C^2+1)^{3/2}}$

Al despejar $x$

$\displaystyle x = \mp \frac{k}{(C^2+1)^{3/2}}$

Sustituyendo esto último en la ecuación primitiva, se tiene que

$\displaystyle y = \mp \frac{k}{(C^2+1)^{3/2}} \pm \frac{C k}{\sqrt{C^2+1}}$

$\displaystyle y = \pm \frac{kC^3}{(C^2+1)^{3/2}}$

Así que, la ecuación envolvente es

$\displaystyle x^{2/3} + y^{2/3} = \frac{k^{2/3}}{(C^2+1)} + \frac{k^{2/3}C^2}{(C^2+1)}$

$\displaystyle x^{2/3} + y^{2/3} = k^{2/3}$

Problema 2. Hallar la curva para la que:

a) La suma de las distancias de los puntos $(a,0)$ y $(-a,0)$ a la recta tangente es igual a $k$ .

b) La suma de las distancias de los puntos $(a,0)$ y $(0,a)$ a la recta tangente es igual a $k$ .

Solución a). Según del enunciado, se tiene la siguiente figura analizada

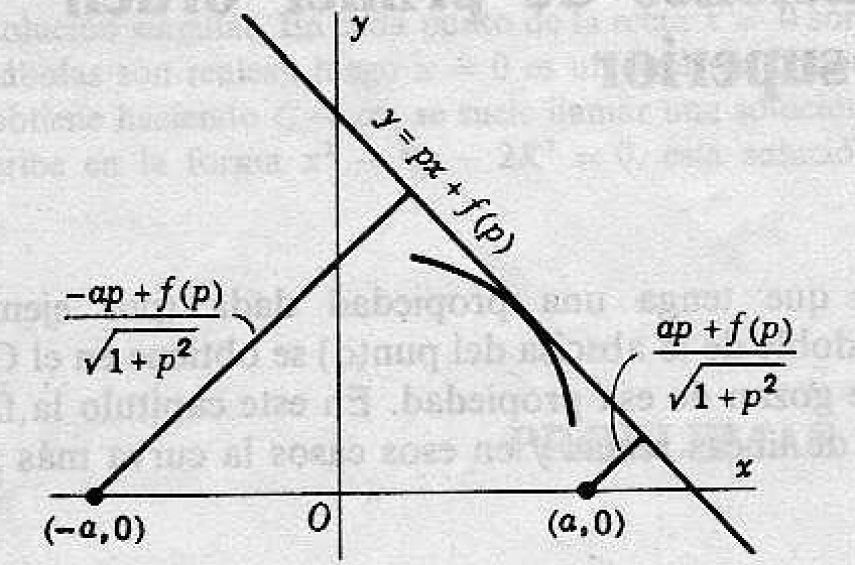
Del punto $(a,0)$ , la primera distancia es

$\displaystyle d_1 = \frac{ap + f(p)}{\sqrt{1+p^2}}$

Y del punto $(-a,0)$ , la segunda distancia es

$\displaystyle d_2 = \frac{-ap + f(p)}{\sqrt{1+p^2}}$

Sumando las distancias (de acuerdo con el enunciado del inciso a))

$\displaystyle d_1 + d_2 = k$

$\displaystyle \frac{ap + f(p)}{\sqrt{1+p^2}} + \frac{-ap + f(p)}{\sqrt{1+p^2}} = k$

$\displaystyle \frac{2 f(p)}{\sqrt{1+p^2}} = k$

Despejando $f(p)$

$\displaystyle f(p) = \frac{1}{2} k\sqrt{1+p^2}$

Sustituyendo en la ecuación de la recta tangente

$\displaystyle y = xp + \frac{1}{2} k \sqrt{1 + p^2}$

Su primitiva es

$\displaystyle y = Cx + \frac{1}{2} k \sqrt{1 + C^2}$

O bien

$(4x^2-k^2)C^2 - 8xyC + 4y^2 - k^2=0$

Determinando la curva (por medio del discriminante)

$b^2 - 4ac=0$

$(-8xy)^2 - 4(4x^2-k^2)(4y^2-k^2) = 0$

$64x^2 y^2 - 4(16x^2 y^2- 4k^2 x^2 - 4k^2 y^2 + k^4) = 0$

$64x^2 y^2 - 64x^2 y^2 + 16k^2 x^2 + 16 k^2 y^2 - 4 k^4 = 0$

$16k^2 x^2 + 16 k^2 y^2 - 4 k^4 = 0$

$x^2 + y^2 = \frac{1}{4} k^2$

Solución b). Según el enunciado, se tiene la siguiente figura analizada

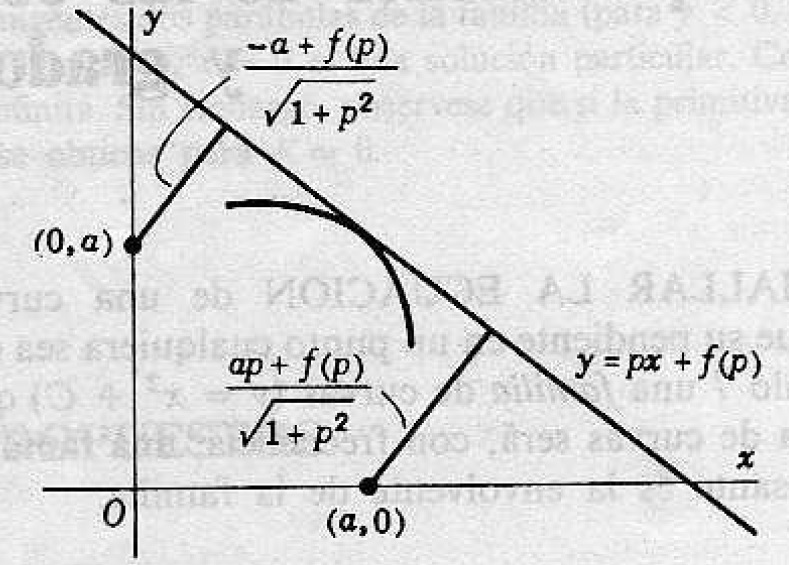
Del punto $(a,0)$ , la primera distancia es

$\displaystyle d_1 = \frac{ap + f(p)}{\sqrt{1+p^2}}$

Y del punto $(0,a)$ , la segunda distancia es

$\displaystyle d_2 = \frac{-a + f(p)}{\sqrt{1+p^2}}$

Sumando las distancias (de acuerdo con el inciso b))

$\displaystyle d_1 + d_2 = k$

$\displaystyle \frac{ap + f(p)}{\sqrt{1+p^2}} + \frac{-a + f(p)}{\sqrt{1+p^2}} = k$

$\displaystyle \frac{ap - a + 2f(p)}{\sqrt{1+p^2}} = k$

Despejando $f(p)$

$\displaystyle f(p) = \frac{1}{2} (a - ap + k \sqrt{1+p^2})$

Sustituyendo en la ecuación de la recta tangente

$\displaystyle y = xp + \frac{1}{2} (a-ap+k \sqrt{1+p^2})$

Determinando su primitiva

$\displaystyle y = Cx + \frac{1}{2} (a-aC+k \sqrt{1+C^2})$

Para obtener la curva, primero se deriva con respecto a $C$ el resultado anterior

$\displaystyle 0 = C + \frac{1}{2} (-a + \frac{Ck}{\sqrt{1+C^2}})$

Despejando $x$

$\displaystyle x= -\frac{1}{2}[-a + \frac{Ck}{(1+C^2)}]$

Sustituyendo en la ecuación primitiva

$\displaystyle y = - \frac{1}{2} C[-a + \frac{Ck}{(1+C^2)}] + \frac{1}{2} (a-aC+k \sqrt{1+C^2})$

$\displaystyle y = \frac{1}{2} (a+ \frac{k}{\sqrt{1+C^2}})$

$(1+C^2)(2y-a)^2 = k^2$

La envolvente es

$b^2 - 4ac = 0$

$\displaystyle x^2 + y^2 - ax - ay = \frac{1}{4} (k^2-2a^2)$

Problema 3. Hallar una curva tal que la tangente en cualquiera de sus puntos $P$ sea la bisectriz del ángulo determinado por la ordenada que pasa por $P$ y la recta que une $P$ con el origen.

Solución. Por medio del enunciado, se tiene la siguiente figura (figura 1.12.4)

Sea $\theta$ el ángulo de inclinación de una tangente y $\phi$ el ángulo de inclinación de $OP$ . Entonces, si $M$ es el pie de la ordenada que pasa por $P$ , en ángulo OPM