Transformadores. Problema 3. Máquinas eléctricas.

Problema. El devanado secundario de un transformador real tiene un voltaje terminal de $v_s (t) = 282.8 \sin{377t} \ (V)$ . La relación de vueltas del transformador es de $100:200 \ (a=0.50)$ . Si la corriente secundaria del transformador es de $i_s (t) = 7.07 \sin{(377t - 36.87)} \ (A)$ , ¿cual es la corriente primaria de este transformador? ¿cual es su regulación de voltaje y su eficiencia? Las impedancias de este transformador referidas al lado primario son

$R_{eq}=0.20 \ (\Omega)$ , $X_eq = 0.80 \ (\Omega)$ , $R_c = 300 \ (\Omega)$ , $X_M = 100 \ (\Omega)$ .

Solución. A continuación, se presenta el circuito equivalente del transformador ideal

Figura 2.3.1 Circuito equivalente de un transformador ideal.

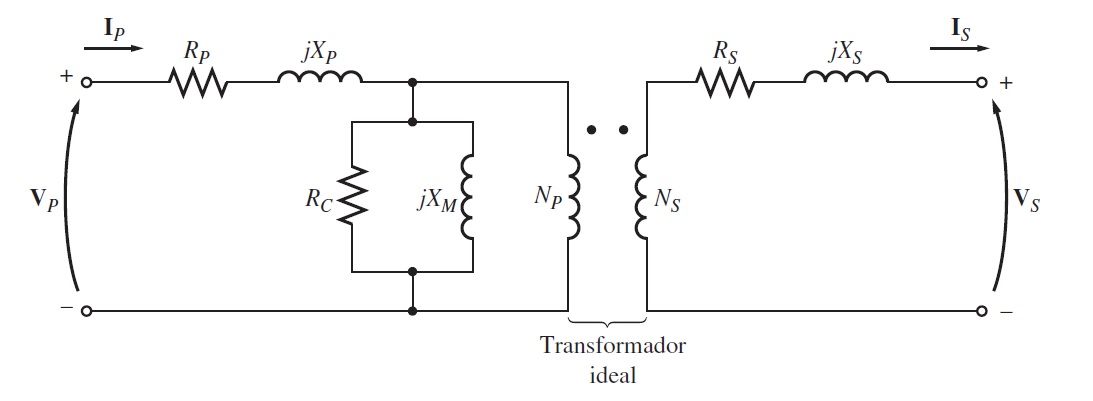
El voltaje terminal se convierte al dominio de la frecuencia

$v_s (t) = 282.8 \sin{377t}$

$\displaystyle \boldsymbol{V_s} = \frac{282.2}{\sqrt{2}} \angle 0 \ (V)$

Y la corriente secundaria también se convierte al dominio de la frecuencia

$i_s (t) = 7.07 \sin{(377t - 36.87)}$

$\displaystyle \boldsymbol{I_s} = \frac{7.07}{\sqrt{2}} \angle (-36.87) \ (A)$

El problema menciona que las impedancias de este transformador referidas al lado primario, por lo que, en la figura 2.3.1, se necesita referir al lado primario, quedando de la siguiente manera

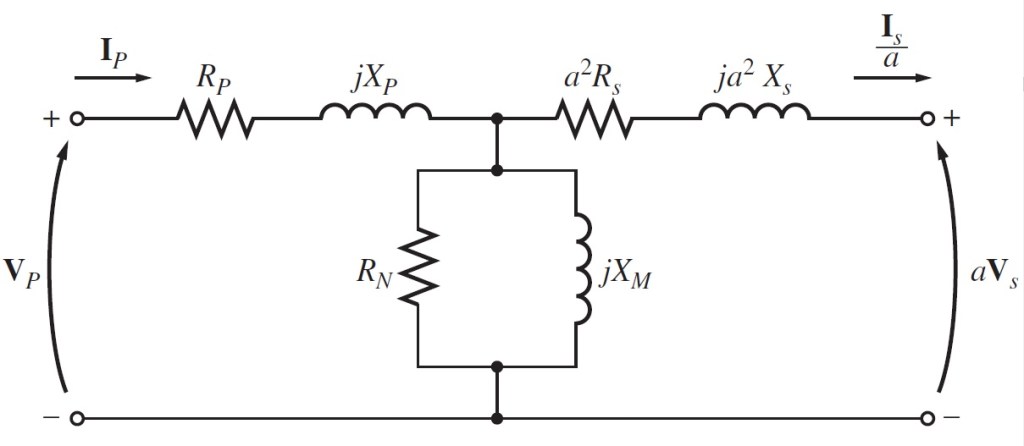
Figura 2.3.2 Circuito equivalente de un transformador referido al lado primario.

Reduciendo un poco más

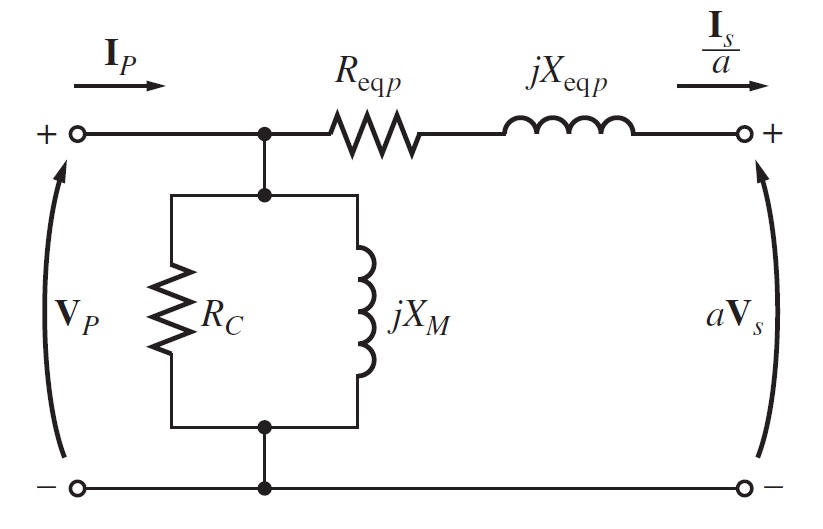
Figura 2.3.3 Modelo aproximado para el transformador referido al lado primario.

Donde, los datos calculados para el último circuito (figura 2.3.3) son:

Resistencia equivalente del lado primario

$\displaystyle R_{eq,P} = R_P + a^2 R_S = R_{eq}$

$R_{eq,P} = 0.20 \ (\Omega)$ R

Reactancia equivalente del lado primario

$\displaystyle X_{eq,P} = X_P + a^2 X_S = X_{eq}$

$\displaystyle X_{eq,P} = 0.80 \ (\Omega)$

Voltaje del lado secundario del transformador referido al lado primario

$\displaystyle a \boldsymbol{V_S} = (0.50) (\frac{282.8}{\sqrt{2}} \angle 0) = \frac{141.4}{\sqrt{2}} \angle 0$

Corriente del lado secundario del transformador referido al lado primario

$\displaystyle \frac{\boldsymbol{I_S}}{a} = \frac{\frac{7.07}{\sqrt{2}} \angle (-36.87)}{0.5} = \frac{14.14}{\sqrt{2}} \angle (-36.87) \ (A)$

Impendancia equivalente del transformador equivalente referido al lado primario

$\displaystyle Z_{eq,P} = R_{eq, P} + j X_{eq,P}$

$\displaystyle X_{eq,P} = 0.20 + j0.80 \ (\Omega)$

Voltaje primario del transformador

$\displaystyle \boldsymbol{V_P} = a \boldsymbol{V_S} + \frac{\boldsymbol{I_S}}{a} R_{eq,P} + j\frac{\boldsymbol{I_S}}{a} X_{eq,P}$

$\displaystyle \boldsymbol{V_P} = \frac{141.4}{\sqrt{2}} \angle 0 + (\frac{14.14}{\sqrt{2}} \angle (-36.87))(0.20) + j(\frac{14.14}{\sqrt{2}} \angle (-36.87))(0.80)$

$\displaystyle \boldsymbol{V_P} = 99.985 \angle 0 + 2 \angle (-36.87) + (1 \angle 90)(7.999 \angle (-36.87)$

$\displaystyle \boldsymbol{V_P} = 99.985 \angle 0 + 2 \angle (-36.87) + (7.999 \angle (53.13)$

$\displaystyle \boldsymbol{V_P} = 99.985 + j0 + 1.6 - j1.2 + 4.799 + j6.399 = 106.384 + j5.199$

$\displaystyle \boldsymbol{V_P} = 106.511 \angle 2.8 \ (V)$

Corriente por pérdidas en el núcleo

$\displaystyle \boldsymbol{I_C} = \boldsymbol{I_{h+e}}$

$\displaystyle \boldsymbol{I_C} = \frac{\boldsymbol{V_P}}{R_C} = \frac{106.511 \angle 2.8 \ (V)}{300 \ (\Omega)}$

$\boldsymbol{I_C} = 0.355 \angle 2.8 \ (A)$

Corriente de magnetización

$\displaystyle \boldsymbol{I_m} = \frac{V_P}{jX_M}$

$\displaystyle \boldsymbol{I_m} = \frac{106.511 \angle 2.8 \ (V)}{j100 \ (\Omega)} = \frac{106.511 \angle 2.8 \ (V)}{100 \angle 90 \ (\Omega)}$

$\displaystyle \boldsymbol{I_m} = 1.065 \angle (-87.2) \ (A)$

Corriente de excitación

$\displaystyle \boldsymbol{I_{Ex}} = \boldsymbol{I_{h+e}} + \boldsymbol{I_m}$

$\displaystyle \boldsymbol{I_{Ex}} = 0.355 \angle 2.8 + 1.065 \angle (-87.2)$

$\displaystyle \boldsymbol{I_{Ex}} = 0.355 + j0.017 + 0.052 -j1.064 = 0.407 - j1.047$

$\displaystyle \boldsymbol{I_{Ex}} = 1.123 \angle (-68.76) \ (A)$

Respondiendo la primera pregunta, la corriente primaria total del transformador es

$\displaystyle \boldsymbol{I_P} = \frac{\boldsymbol{I_S}}{a} + \boldsymbol{I_{Ex}}$

$\displaystyle \boldsymbol{I_P} = \frac{14.14}{\sqrt{2}} \angle (-36.87) + 1.123 \angle (-68.76) = 9.998 \angle (-36.87) + 1.123 \angle (-68.76)$

$\displaystyle \boldsymbol{I_P} = 7.998 - j5.999 + 0.407 - j1.047 = 8.405 - j7.046$

$\displaystyle \therefore \boldsymbol{I_P} = 10.968 \angle (-39.97) \ (A)$

La regulación de voltaje de este transformador es

$\displaystyle RV = \frac{V_P - a V_S}{a V_S} \times 100$ %

$\displaystyle RV = \frac{106.511 - \frac{141.4}{\sqrt{2}}}{\frac{141.4}{\sqrt{2}}} \times 100$ %

$\therefore RV = 6.53$ %

Y la eficiencia de este transformador se calcula determinando la potencia de entrada

$P_{ent} = V_P I_P \cos{\theta_P}$

$P_{ent} = (106.303)(10.968) \cos{(2.8+39.97)}$

$P_{ent} = 855.893 \ (W)$

Y la potencia de salida

$P_{sal} = V_S I_S \cos{\theta_S}$

$P_{sal} = (\frac{282.8}{\sqrt{2}})(\frac{7.07}{\sqrt{2}}) \cos{36.87}$

$P_{sal} = 799.757 \ (W)$

Entonces

$\displaystyle \eta = \frac{P_{sal}}{P_{ent}} \times 100$

$\displaystyle \eta = \frac{799.757}{855.893} \times 100$

$\displaystyle \therefore \eta = 93.44$ %

Transformadores. Problema 3. Máquinas eléctricas.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Transformadores. Problema 3. Máquinas eléctricas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta