Transformadores. Problema 13. Máquinas eléctricas.

Problema. Un generador monofásico de 13.8 (kV) suministra potencia a una carga a través de una línea de transmisión. La impedancia de la carga es $Z_{carga} = 500 \angle 36.87 \ (\Omega)$ y la impedancia de la línea de transmisión es $Z_{linea} = 60 \angle 60 \ (\Omega)$ .

a) Si se conecta el generador directamente a la carga (figura 2.13.1), ¿cuál es la razón entre el voltaje de la carga y el voltaje generado? ¿Cuáles son las pérdidas de transmisión del sistema?

b) ¿Qué porcentaje de la potencia suministrada por la fuente alcanza la carga? (¿cuál es la eficiencia del sistema de transmisión?)

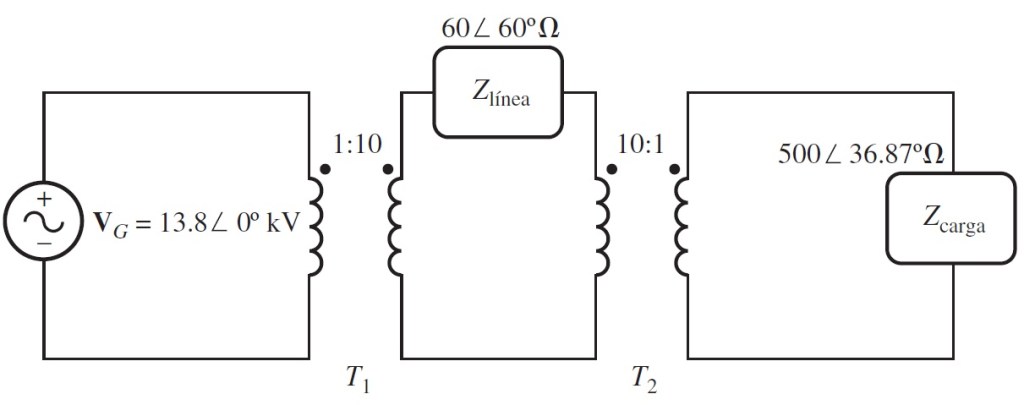
c) Si se coloca un transformador 1:10 a la salida del generador y un transformador 10:1 en el extremo de la línea de transmisión donde está la carga, ¿cuál es la nueva relación entre el voltaje de la carga y el voltaje generado? ¿Ahora cuáles son las pérdidas de transmisión del sistema? (Nota: Se puede suponer que los transformadores son ideales).

d) ¿Qué porcentaje de la potencia suministrada por la fuente alcanza ahora la carga?

e) Compare las eficiencias del sistema de transmisión con o sin transformadores.

Figura 2.13.1 Circuito sin transformadores.

Figura 2.13.2 Circuito con transformadores.

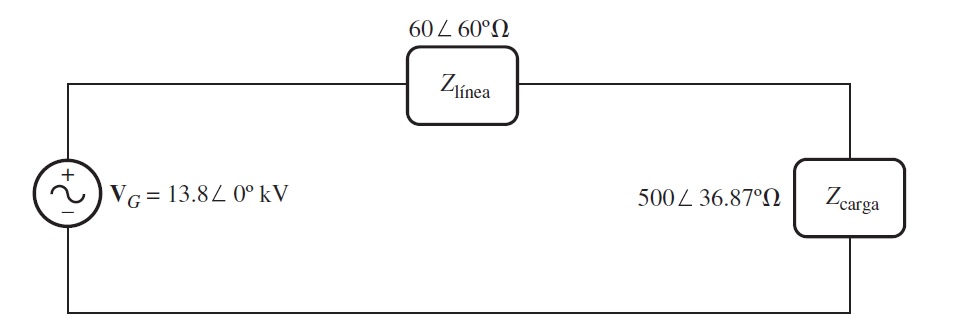
Solución a). Se calcula la corriente de linea

$\displaystyle \boldsymbol{I_{linea}} = \boldsymbol{I_{carga}} = \boldsymbol{I_{G}}$

$\displaystyle \boldsymbol{I_{linea}} = \frac{\boldsymbol{V}}{Z_{linea} + Z_{carga}}$

$\displaystyle \boldsymbol{I_{linea}} = \frac{13800 \angle 0}{60 \angle 60 + 500 \angle 36.87} = \frac{13800 \angle 0}{30+j51.9615+400+j300}$

$\displaystyle \boldsymbol{I_{linea}} = \frac{13800 \angle 0}{430 + j351.9615} = \frac{13800}{555.6700 \angle 39.9}$

$\displaystyle \boldsymbol{I_{linea}} =24.8346 \angle (-39.3) \ (A)$

Después, el voltaje de carga es

$\displaystyle \boldsymbol{V_{carga}} = \boldsymbol{I_{carga}} Z_{carga}$

$\displaystyle \boldsymbol{V_{carga}} = (24.8346 \angle (-39.6))(500 \angle 36.87)$

$\displaystyle \boldsymbol{V_{carga}} = 12417.3 \angle (-2.43) \ (V)$

Por tanto, la regulación de voltaje es

$\displaystyle a = \frac{V_{carga}}{V} = \frac{12417.3}{13800}$

$\displaystyle \therefore a = 0.9$

Para conocer las pérdidas de transmisión del sistema, se sabe que la resistencia en la transmisión de línea es

$R_{linea} = |Z_{linea}| \cos{\theta}$

$R_{linea} = (60) \cos{60}$

$R_{linea} = 30 \ (\Omega)$

Así

$\displaystyle P_{perdida} = (I_{linea})^2 R_{linea}$

$\displaystyle P_{perdida} = (24.8346)^2 (30)$

$\displaystyle \therefore P_{perdida} = 18502.7207 \ (W) = 18.503 \ (kW)$

Solución b). Para calcular el porcentaje, se debe tener en cuenta la potencia perdida en la transmisión del sistema y la potencia de salida

$P_{sal} = V_S I_S \cos{\theta} = V_{carga} I_{carga} \cos{\theta}$

$P_{sal} = (12417.3)(24.8346) \cos{39.3}$

$P_{sal} = 238,635.8 = 238.636 \ (kW)$

Entonces

$\displaystyle \eta = \frac{P_{sal}}{P_{sal} + P_{perdida}} \times 100$ %

$\displaystyle \eta = \frac{238.636 \times 10^3}{238.636 \times 10^3 + 18.503 \times 10^3} \times 100$ %

$\displaystyle \eta = 92.80$ %

Solución c). Para responder las preguntas de este inciso, se realiza lo siguiente:

Eliminación del transformador $T_2$ referido la carga al nivel de voltaje en la línea de transmisión.

*Figura 2.13.3 Eliminando un transformador referido la carga al nivel de voltaje de la línea de transmisión.*

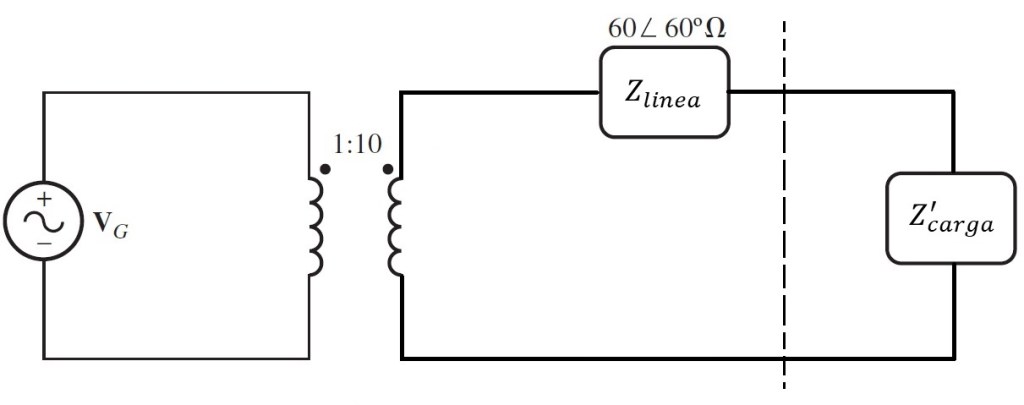
Cálculo de la impedancia de carga

$\displaystyle Z_{carga}' = a^2 Z_{carga}$

$\displaystyle Z_{carga}' = (\frac{10}{1})^2 (500 \angle 36.87)$

$\displaystyle Z_{carga}' = 50000 \angle 36.87 \ (\Omega)$

La impedancia de linea permanece intacta por el momento.

Eliminación del transformador $T_1$ refiriendo los elementos de la línea de transmisión y carga equivalente al voltaje de la línea de transmisión del lado de la fuente.

*Figura 2.13.4 Eliminando el segundo transformador referido a los elementos de la línea de transmisión y carga equivalente al voltaje de la línea de transmisión del lado de la fuente.*

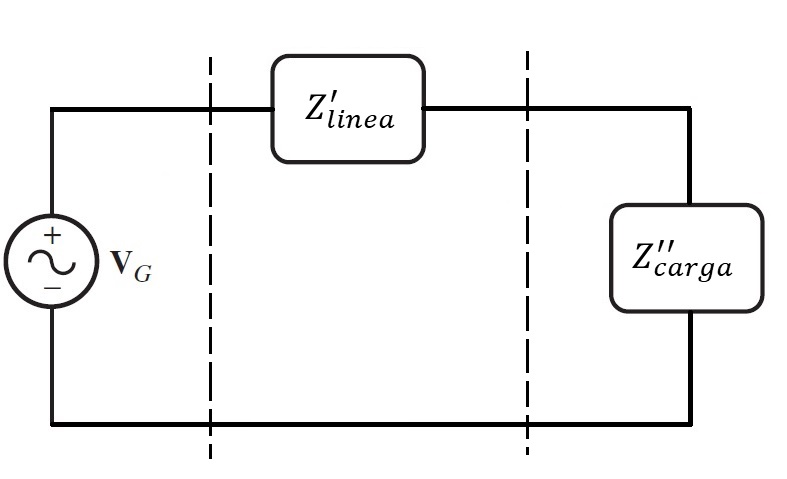
Para este paso, primero se calcula la nueva impedancia de linea

$\displaystyle Z_{linea}' = a^2 Z_{linea}$

$\displaystyle Z_{linea}' = (\frac{1}{10})^2 (60 \angle 60)$

$\displaystyle Z_{linea}' = 0.6 \angle 60 \ (\Omega)$

después, se calcula la impedancia de carga

$\displaystyle Z_{carga}'' = a^2 Z_{carga}'$

$\displaystyle Z_{carga}'' = (\frac{1}{10})^2 (50000 \angle 36.87)$

$\displaystyle Z_{carga}'' = 500 \angle 36.87$

Continuando con el problema, el fasor de la corriente del generador se determina de la siguiente manera

$\displaystyle \boldsymbol{I_{G}} = \frac{\boldsymbol{V_G}}{Z_{linea}' + Z_{carga}''}$

$\displaystyle \boldsymbol{I_{G}} = \frac{13800 \angle 0}{0.6 \angle 60 + 500 \angle 36.87}$

$\displaystyle \boldsymbol{I_{G}} = \frac{13800 \angle 0}{0.3 + j0.52 + 400 +j300}$

$\displaystyle \boldsymbol{I_{G}} = \frac{13800 \angle 0}{400.3 + j300.52} = \frac{13800 \angle 0}{500.552 \angle 36.9}$

$\displaystyle \boldsymbol{I_{G}} = 27.57 \angle (-36.9) \ (A)$

La corriente de línea se calcula como

$N_{P1} \boldsymbol{I_G} = N_{S1} \boldsymbol{I_{linea}}$

$\displaystyle \boldsymbol{I_{linea}} = \frac{N_{P1} \boldsymbol{I_G}}{N_{S1}}$

$\displaystyle \boldsymbol{I_{linea}} = \frac{(1)(27.57 \angle (-36.9))}{10}$

$\displaystyle \boldsymbol{I_{linea}} = 2.757 \angle (-36.9) \ (A)$

La corriente de carga es

$N_{P2} \boldsymbol{I_{linea}} = N_{S2} \boldsymbol{I_{carga}}$

$\displaystyle \boldsymbol{I_{carga}} = \frac{N_{P2} \boldsymbol{I_G}}{N_{S2}}$

$\displaystyle \boldsymbol{I_{carga}} = \frac{(10)(2.757 \angle (-36.9)}{1}$

$\displaystyle \boldsymbol{I_{carga}} = 27.57 \angle (-36.9) \ (A)$

Respondiendo la primera pregunta de este inciso, el voltaje de carga es

$\boldsymbol{V_{carga}} = \boldsymbol{I_{carga}} Z_{carga}$

$\boldsymbol{V_{carga}} = (27.57 \angle (-36.9))(500 \angle 36.87)$

$\displaystyle \therefore \boldsymbol{V_{carga}} = 13785 \angle (-0.03) \ (V)$

Y recordando que el voltaje generado es

$\displaystyle \boldsymbol{V_G} = 13.8 \angle 0 \ (kV) = 13800 \angle 0 \ (V)$

La relación de vueltas entre el voltaje de carga y el voltaje generado es

$\displaystyle a = \frac{V_{carga}}{V}$

$\displaystyle a = \frac{13785}{13800}$

$\displaystyle \therefore a = 0.9989$

Y contestando la segunda pregunta, la pérdida de transmisión en el sistema es

$P_{perdida} = (I_{linea})^2 R_{linea} = (I_{linea})^2 \cdot |Z_{linea}| \cos{\theta}$

$P_{perdida} = (2.757)^2 (60 \cos{60})$

$\therefore P_{perdida} = 228.032 \ (W)$

Solución d). Para conocer el porcentaje, se debe tomar en cuenta la potencia perdida y la potencia de salida

$P_{sal} = V_S I_S \cos{\theta} = V_{carga} I_{carga} \cos{\theta}$

$P_{sal} = (13785)(27.57) \cos{(-36.9)}$

$P_{sal} = 303922.114 \ (W)$

Finalmente

$\displaystyle \eta = \frac{P_{sal}}{P_{sal} + P_{perdida}} \times 100$ %

$\displaystyle \eta = \frac{303922.114}{303922.114+ 228.032} \times 100$ %

$\displaystyle \eta = 99.93$ %

Solución e). Elevando el voltaje de transmisión del sistema de potencia, se reducen las pérdidas de transmisión. El voltaje de carga cayó muy poco en el sistema con transformadores en comparación con el sistema sin transformadores. Esto se observa con los resultados de la eficiencia.

Transformadores. Problema 13. Máquinas eléctricas.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Transformadores. Problema 13. Máquinas eléctricas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta