Transformadores. Problema 18. Máquinas eléctricas.

Problema. Dos de las fases de una línea de distribución trifásica de 14.4 (kV) dan servicio a un camino rural remoto (también esta disponible el neutro). Un granjero tiene un alimentador de 480 (V) que suministra 200 (kW) a un $FP =0.85$ en retraso de estas cargas trifásicas, más 60 (kW) en un $FP = 0.90$ en retraso de las cargas monofásicas. Las cargas monofásicas se distribuyen uniformemente entre las tres fases. Suponiendo que se utiliza la conexión $Y$ abierta – $\Delta$ abierta suministrar potencia a su granja, encuentre los voltajes y corrientes en cada uno de los dos transformadores. También calcule la potencia real y reactiva suministradas por cada transformador. ¿Cuál es el valor nominal mínimo requerido (kVA) de cada transformador?

Solución. El sistema de potencia de la granja es ilustrado a continuación

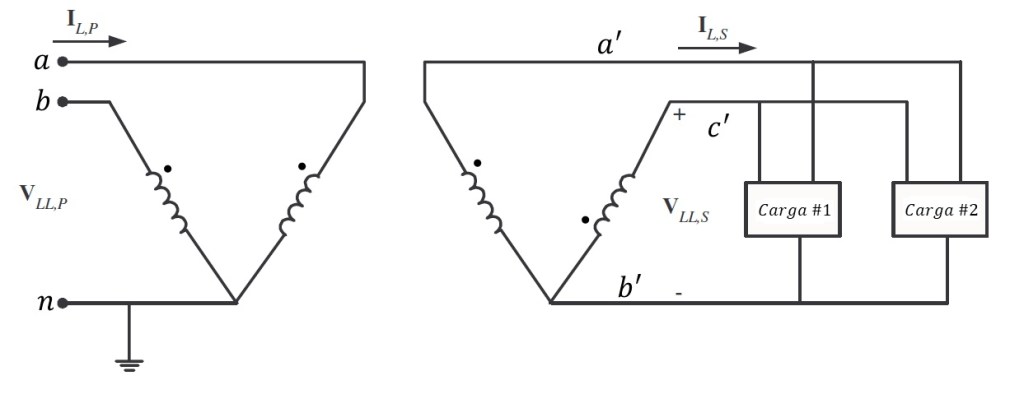
Después, las cargas en cada fase están balanceadas. En la carga #1

$P_1 = 200 \ (kW)$ y $\theta_1 = \cos^{-1}{(0.85)} = 31.79$ °

$Q_1 = P_1 \tan{\theta_1} = (200 \times 10^3)\tan{(31.79)}$

$\displaystyle Q_1 = 123.9569 \times 10^3 \ (var) = 123.9569 \ (kvar)$

$\displaystyle S_1 = \sqrt{P_1^2 + Q_1^2} = \sqrt{(200 \times 10^3)^2 + (123.9569)^2}$

$\displaystyle S_1 = 235.2983 \times 10^3 \ (VA) = 235.2983 \ (kVA)$

Y en la carga #2

$P_2 = 60 \ (kW)$ y $\theta_2 = \cos^{-1}{(0.9)} = 25.84$ °

$Q_2 = P_2 \tan{\theta_2} = (60 \times 10^3)\tan{(25.84)}$

$\displaystyle Q_2 = 29.0568 \times 10^3 \ (var) = 29.0568 \ (kvar)$

$\displaystyle S_2 = \sqrt{P_2^2 + Q_2^2} = \sqrt{(60 \times 10^3)^2 + (29.0568)^2}$

$\displaystyle S_2 = 66.6656 \times 10^3 \ (VA) = 66.6656 \ (kVA)$

La potencia total es

$P_T = P_1 + P_2$

$P_T = 200\times 10^3 + 60 \times 10^3$

$P_T = 260\times 10^3 \ (W) = 260 \ (kW)$

La potencia reactiva total es

$Q_T = Q_1 + Q_2$

$Q_T = 123.9569 \times 10^3 + 29.0568 \times 10^3$

$Q_T = 153.0137 \times 10^3 \ (var) = 153.0137 \ (kvar)$

La potencia aparente total es

$S_T = S_1 + S_2$

$S_T = 235.2983 \times 10^3 + 666.6656 \times 10^3$

$S_T = 301.9639 \times 10^3 \ (VA) = 301.9639 \ (kVA)$

Calculando el factor de potencia total

$\displaystyle FP = \cos{\theta} = \cos{\left[\arctan{\left(\frac{Q_T}{P_T} \right)} \right]}$

$\displaystyle FP = \cos{\left[\arctan{\left(\frac{153.0137\times 10^3}{260 \times 10^3} \right)} \right]}$

$\displaystyle FP = 0.862$ (en retraso)

Y el ángulo theta es

$\cos{\theta} = FP$

$\theta = \cos^{-1}{FP} = \cos^{-1}{(0.862)}$

$\theta = 30.46$ °

Ahora, la conexión $Y$ , el voltaje de fase es

$\displaystyle V_{\phi} = \frac{V_L}{\sqrt{3}}$

Y, la conexión en $\Delta$ , el voltaje de fase es

$V_{\phi} = V_L$

Así, se puede analizar los devanados del transformador en el lado primario y en el lado secundario. En el lado primario, se tiene la conexión $Y$ , por lo que sus datos a tomar en cuenta son los siguientes:

Voltaje de fase en el devanado primario

$\displaystyle V_{\phi P} = \frac{V_{LP}}{\sqrt{3}}$

$\displaystyle V_{\phi P} = \frac{14.4 \times 10^3}{\sqrt{3}}$

$\displaystyle V_{\phi P} = 8313.8439 \ \times 10^3 \ (V) = 8313.8439 \ (kV)$

Voltaje primario en la conexión A

$\displaystyle \boldsymbol{V}_A = V_{\phi P} \angle 0 \ (V)$

$\displaystyle \therefore \boldsymbol{V}_A = 8313.8439 \angle 0 \ (V)$

Voltaje primario en la conexión B

$\displaystyle \boldsymbol{V}_B = V_{\phi P} \angle (-120) \ (V)$

$\displaystyle \therefore \boldsymbol{V}_B = 8313.8439 \angle (-120) \ (V)$

Corriente de fase en el devanado primario

$\displaystyle I_{\phi P} = I_{LP} = \frac{S_T}{V_{LP}}$

$\displaystyle I_{\phi P} = \frac{301.9639 \times 10^3}{14.4\times 10^3}$

$\displaystyle I_{\phi P} = 20.9697 \ (A)$

Corriente primaria de la conexión A

$\displaystyle \boldsymbol{I}_{AP} = I_{\phi P} \angle (-\theta-30) \ (A)$

$\displaystyle \boldsymbol{I}_{AP} = 20.9697 \angle (-30.46-30) \ (A)$

$\displaystyle \therefore \boldsymbol{I}_{AP} = 20.9697 \angle (-60.46) \ (A)$

Corriente primaria de la conexión B

$\displaystyle \boldsymbol{I}_{BP} = I_{\phi P} \angle (-\theta-150) \ (A)$

$\displaystyle \boldsymbol{I}_{BP} = 20.9697 \angle (-30.46-150) \ (A)$

$\displaystyle \therefore \boldsymbol{I}_{BP} = 20.9697 \angle (-180.46) \ (A)$

Corriente primaria de la conexión neutro

$\displaystyle \boldsymbol{I}_n = I_{\phi P} \angle (-\theta+90) \ (A)$

$\displaystyle \boldsymbol{I}_n = 20.9697 \angle (-30.46+90) \ (A)$

$\displaystyle \therefore \boldsymbol{I}_n = 20.9697 \angle (59.54) \ (A)$

En el lado secundario, se tiene la conexión $\Delta$ , por lo que sus datos a tomar en cuenta son los siguientes:

Voltaje de fase en el devanado secundario

$\displaystyle V_{\phi S} = V_{LP}$

$\displaystyle V_{\phi S} = 480 \ (V)$

Voltaje secundario en la conexión A

$\displaystyle \boldsymbol{V}_{AS} = V_{\phi S} \angle 0 \ (V)$

$\displaystyle \therefore \boldsymbol{V}_{AS} = 480 \angle 0 \ (V)$

Voltaje primario en la conexión B

$\displaystyle \boldsymbol{V}_{BS} = V_{\phi S} \angle (-120) \ (V)$

$\displaystyle \therefore \boldsymbol{V}_{BS} = 480 \angle (-120) \ (V)$

Corriente de fase en el devanado secundario. Tomando la fórmula de la potencia en el lado secundario

$\displaystyle P_S = V_S I_S \cos{\theta} \rightarrow I_S = \frac{P_S}{V_S \cos{\theta}}$

Luego

$\displaystyle I_{\phi S} = \frac{P_{\phi S}}{V_{\phi S} \cos{\theta}}$

Convirtiéndolo a corriente de linea en el devanado secundario

$\displaystyle I_{LS} = \frac{\frac{P_{LS}}{3}}{\frac{V_{LS}}{\sqrt{3}} \cos{\theta}} \rightarrow I_{LS} = \frac{P_{LS}}{\sqrt{3} V_{LS} \cos{\theta}}$

$\displaystyle I_{LS} = \frac{260 \times 10^3}{\sqrt{3} \cdot (480) \cdot (0.862}$

$\displaystyle I_{LS} = 362.7974 \ (A)$

Por tanto,

$I_{\phi S} = I_{LS} = 362.7974 \ (A)$

Corriente secundaria de la conexión A

$\displaystyle \boldsymbol{I}_{AS} = I_{\phi S} \angle (-\theta-30) \ (A)$

$\displaystyle \boldsymbol{I}_{AS} = 362.7974 \angle (-30.46-30) \ (A)$

$\displaystyle \therefore \boldsymbol{I}_{AS} = 362.7974 \angle (-60.46) \ (A)$

Corriente secundaria de la conexión B

$\displaystyle \boldsymbol{I}_{BS} = I_{\phi S} \angle (-\theta-150) \ (A)$

$\displaystyle \boldsymbol{I}_{BS} = 362.7974 \angle (-30.46-150) \ (A)$

$\displaystyle \therefore \boldsymbol{I}_{BS} = 362.7974 \angle (-180.46) \ (A)$

Corriente secundaria de la conexión C

$\displaystyle \boldsymbol{I}_{CS} = I_{\phi S} \angle (-\theta+90) \ (A)$

$\displaystyle \boldsymbol{I}_{CS} = 362.7974 \angle (-30.46+90) \ (A)$

$\displaystyle \therefore \boldsymbol{I}_{CS} = 362.7974 \angle (59.54) \ (A)$

Con todos estos datos se tienen mostrados en la siguiente figura

Figura 2.18.2 Representando los valores de las corrientes y voltajes en cada conexión.

Por último, se calculará el valor nominal mínimo requerido kVA para cada transformador. Primero se determinan las potencias reales. En el primer transformador

$P_A = V_{AS} I_A \cos{\theta}$