22 mayo, 201930 abril, 2019 Cesar Reyes máquinas eléctricas

Transformadores. Problema 19. Máquinas eléctricas.

Problema. Pruebe que el sistema trifásico de voltajes en el secundario del transformador $Y-\Delta$ que se muestra en la siguiente figura retrasa 30° el sistema de voltaje trifásico en el primario del transformador.

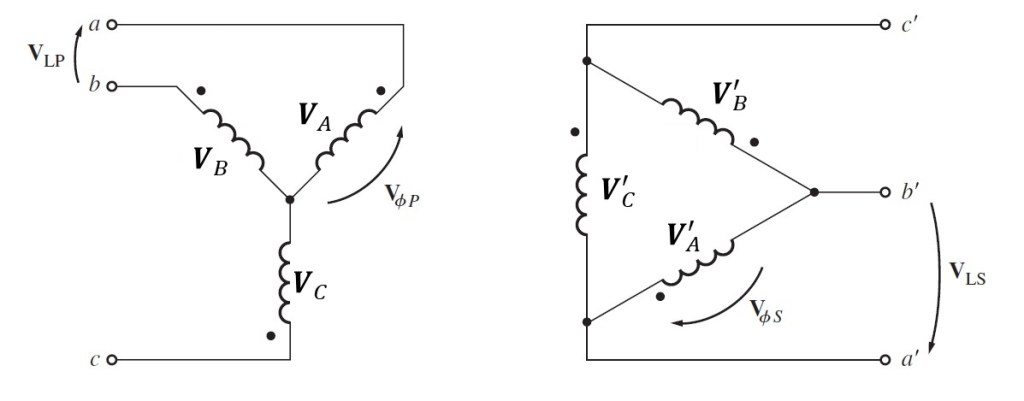
Figura 2.19.1 Conexión Y-Δ (ye-delta).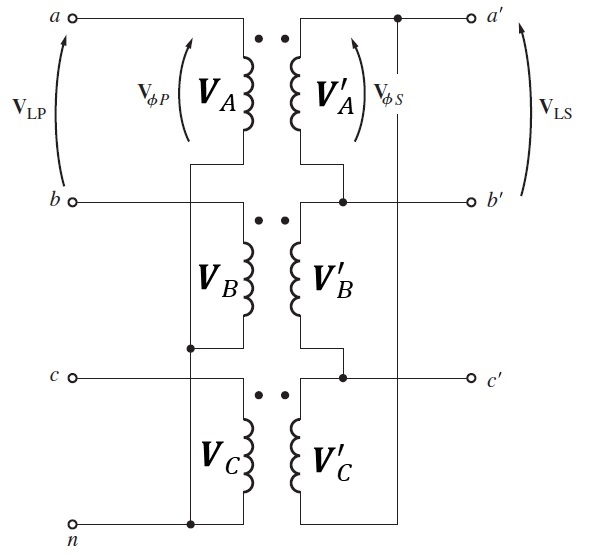
Figura 2.19.2 Conexión Y-Δ (ye-delta).

Solución. Suponiendo que los voltajes de fase en el lado primario son

$\boldsymbol{V}_A = V_{\phi P} \angle 0 \ (V)$

$\boldsymbol{V}_B = V_{\phi P} \angle (-120) \ (V)$

$\boldsymbol{V}_C = V_{\phi P} \angle (120) \ (V)$

Entonces, los voltajes de fase en el lado secundario son

$\boldsymbol{V}_A' = a \boldsymbol{V}_{A} = V_{\phi S} \angle 0 \ (V)$

$\boldsymbol{V}_B' = a \boldsymbol{V}_{B} = V_{\phi S} \angle (-120) \ (V)$

$\boldsymbol{V}_C' = a \boldsymbol{V}_{C} = V_{\phi S} \angle (120) \ (V)$

que también se puede expresar de la siguiente manera

$\displaystyle \boldsymbol{V}_A' = a \boldsymbol{V}_{A} = \frac{V_{\phi P}}{a} \angle 0 \ (V)$

$\displaystyle \boldsymbol{V}_B' = a \boldsymbol{V}_{B} = \frac{V_{\phi P}}{a} \angle (-120) \ (V)$

$\displaystyle \boldsymbol{V}_C' = a \boldsymbol{V}_{C} = \frac{V_{\phi P}}{a} \angle (120) \ (V)$

Si este es un banco de transformadores en $Y-\Delta$ , el voltaje de línea en el lado primario es

$\displaystyle \boldsymbol{V}_{ab} = \boldsymbol{V}_a - \boldsymbol{V}_b$

$\displaystyle \boldsymbol{V}_{ab} = V_{\phi P} \angle 0 - V_{\phi P} \angle (-120)$

$\displaystyle \boldsymbol{V}_{ab} = V_{\phi P} (1 \angle 0 - 1 \angle (-120))$

$\displaystyle \boldsymbol{V}_{ab} = V_{\phi P} (1 + j0 +0.5 +j\frac{\sqrt{3}}{2})$

$\displaystyle \boldsymbol{V}_{ab} = V_{\phi P} (1.5 +j\frac{\sqrt{3}}{2})$

$\displaystyle \boldsymbol{V}_{ab} = V_{\phi P} (\sqrt{3} \angle 30)$

$\displaystyle \therefore \boldsymbol{V}_{ab} = \sqrt{3} V_{\phi P} \angle 30$

Y el voltaje secundario es

$\displaystyle \boldsymbol{V}_{a'b'} = a \boldsymbol{V}_{A}$

$\displaystyle \boldsymbol{V}_{a'b'} = V_{\phi S} \angle 0 \ (V)$

$\displaystyle \therefore \boldsymbol{V}_{a'b'} = \frac{V_{\phi P}}{a} \angle 0 \ (V)$

Se observa que el voltaje de línea en el lado secundario retrasa el voltaje de línea en el lado primario por 30°.

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.