Transformadores. Problema 20. Máquinas eléctricas.

Problema. Demuestre que el sistema trifásico de voltajes en el secundario del transformador $\Delta - Y$ que se muestran en las siguientes figuras retrasa 30° el sistema de voltajes trifásico en el primario del transformador.

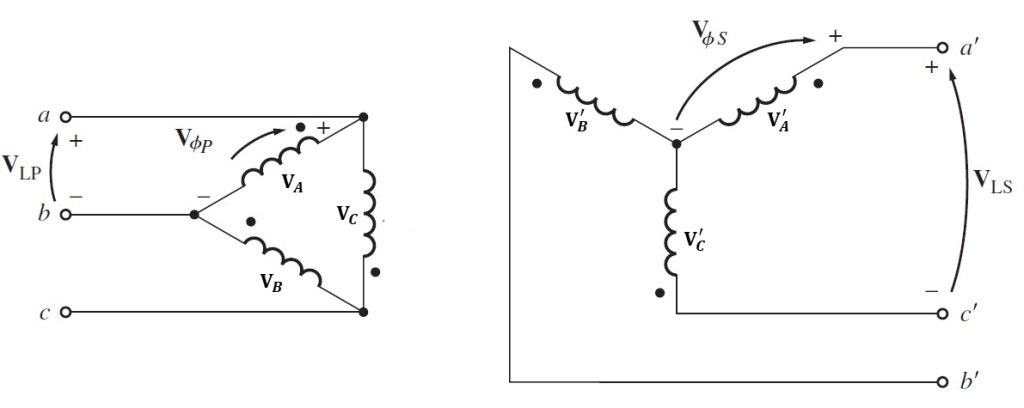
Figura 2.20.1 Conexión Δ-Y (delta – ye).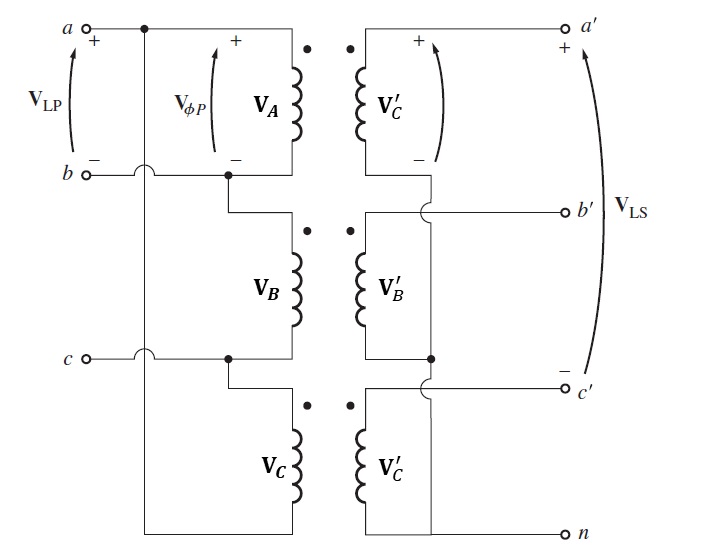
Figura 2.20.2 Conexión Δ-Y (delta – ye).

Solución. Suponiendo que los voltajes de fase en el lado primario son

$\displaystyle \boldsymbol{V}_A = V_{\phi P} \angle 0 \ (V)$

$\displaystyle \boldsymbol{V}_B = V_{\phi P} \angle (-120) \ (V)$

$\displaystyle \boldsymbol{V}_C = V_{\phi P} \angle (120) \ (V)$

Entonces, los voltajes de fase en el lado secundario son

$\displaystyle \boldsymbol{V}_{A}' = a \boldsymbol{V}_A = V_{\phi S} \angle 0 \ (V)$

$\displaystyle \boldsymbol{V}_{B}' = a \boldsymbol{V}_B = V_{\phi S} \angle (-120) \ (V)$

$\displaystyle \boldsymbol{V}_{C}' = a \boldsymbol{V}_C = V_{\phi S} \angle (120) \ (V)$

Dado que este banco de transformadores $\Delta - Y$ , el voltaje de línea $\boldsymbol{V}_{ab}$ en el lado primario es igual a

$\displaystyle \boldsymbol{V}_A = V_{\phi P} \angle 0 \ (V)$

El voltaje de línea en el lado secundario es

$\displaystyle \boldsymbol{V}_{a'b'} = \boldsymbol{V}_A - \boldsymbol{V}_C$

$\displaystyle \boldsymbol{V}_{a'b'} = V_{\phi P} \angle 0 - V_{\phi P} \angle 120$

$\displaystyle \boldsymbol{V}_{a'b'} = V_{\phi P}(1 \angle 0 - 1 \angle 120)$

$\displaystyle \boldsymbol{V}_{a'b'} = V_{\phi P}(1 + j0 + 0.5 - j \frac{\sqrt{3}}{2})$

$\displaystyle \boldsymbol{V}_{a'b'} = V_{\phi P}(1.5 - j \frac{\sqrt{3}}{2})$

$\displaystyle \boldsymbol{V}_{a'b'} = V_{\phi P}(\sqrt{3} \angle -30)$

$\displaystyle \boldsymbol{V}_{a'b'} = \sqrt{3} V_{\phi P} \angle -30$

Se observa que el voltaje de línea en el lado secundario retrasa el voltaje de línea en el lado primario 30°.

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.

Transformadores. Problema 20. Máquinas eléctricas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta