El rectángulo y la curva. Máximos y mínimos. Aplicaciones de cálculo diferencial.

Problema. Probar que el rectángulo de área máxima con base sobre el eje OX y dos vértices sobre la curva $y = e^{-x^2}$ , deberá tener estos dos vértices sobre los puntos de inflexión de la curva.

*Figura 4.12.1 Representación gráfica del problema.*

Solución. Analizando la curva y el rectángulo

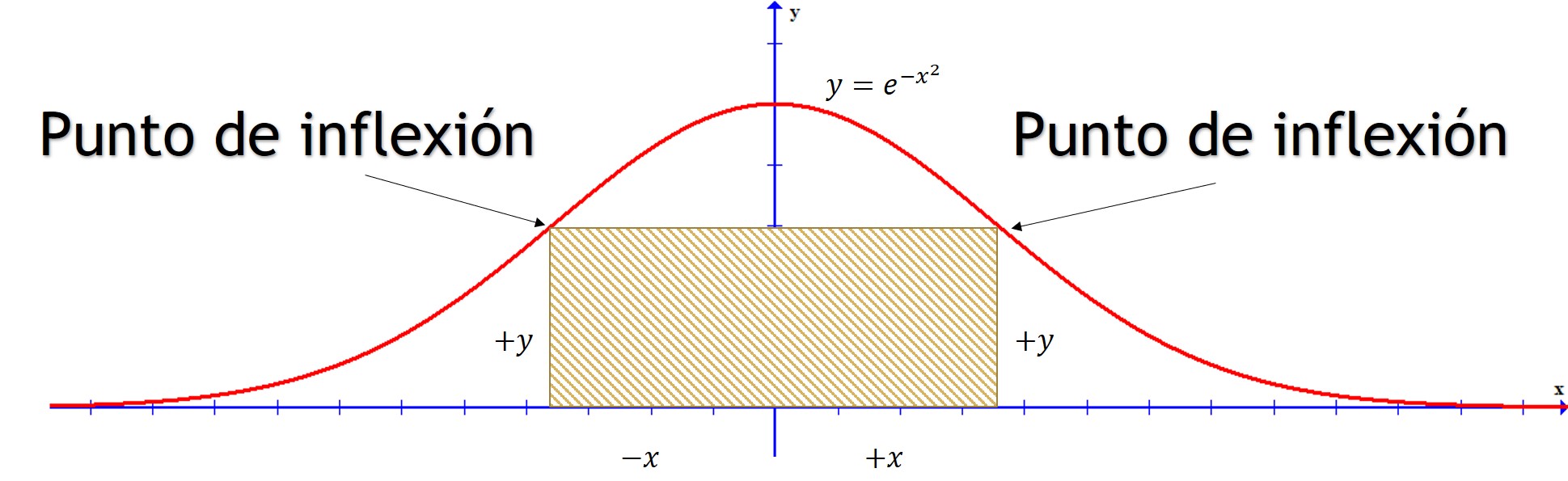
*Figura 4.12.2 Localizando los puntos de inflexión.*

Paso 1. El área del rectángulo es

$A = \text{base} \cdot \text{altura}$

$A=(2x)(y)$

$A=2xy$

Paso 2. La curva tiene la siguiente ecuación

$\displaystyle y = e^{-x^2}$

Paso 3. Sustituyendo la ecuación “ $y$ ” en la expresión del área, se tiene que

$A = 2xy$

$\displaystyle A = 2x(e^{-x^2})$

$\displaystyle A = 2xe^{-x^2}$

Paso 4. Derivando la ecuación “ $A$ ” con respecto a la variable independiente

$\displaystyle \frac{d}{dx} (A) = \frac{d}{dx} (2xe^{-x^2})$

$\displaystyle \frac{dA}{dx} = 2 \frac{d}{dx} (xe^{-x^2})$

$\displaystyle \frac{dA}{dx} = 2(e^{-x^2} - 2x^2 e^{-x^2})$

$\displaystyle \frac{dA}{dx} = 2e^{-x^2} - 4x^2 e^{-x^2}$

Paso 5. Si $\displaystyle \frac{dA}{dx} = 0$

$\displaystyle \frac{dA}{dx} = 2e^{-x^2} - 4x^2 e^{-x^2}$

$\displaystyle 0 = 2e^{-x^2} - 4x^2 e^{-x^2}$

$\displaystyle 4x^2 e^{-x^2} = 2e^{-x^2}$

$\displaystyle \frac{4}{2} x^2 = \frac{e^{-x^2}}{e^{-x^2}}$

$2x^2 = 1$

$\displaystyle x = \pm \sqrt{\frac{1}{2}}$

Sustituyendo el valor de “ $x$ ” en la ecuación de la curva (ecuación “ $y$ ”)

$\displaystyle y = e^{-x^2}$

$\displaystyle y = e^{- \left( \pm \frac{1}{\sqrt{2}} \right)^2}$

$\displaystyle y = e^{-\frac{1}{2}}$

$\displaystyle y = \frac{1}{\sqrt{e}}$

De los valores de “ $x$ ” y “ $y$ ” calculados, se determina el valor del área

$A = 2xy$

$\displaystyle A = 2 \left(\frac{1}{\sqrt{2}} \right) \left(\frac{1}{\sqrt{e}} \right)$

$\displaystyle A = \frac{\sqrt{2} e}{e} \approx 0.8578 \ (u^2)$

Paso 6. Determinando la segunda derivada (tomando el resultado de la primera derivada del área)

$\displaystyle \frac{d}{dx} \left(\frac{dA}{dx} \right) = \frac{d}{dx} \left(2e^{-x^2} - 4x^2 e^{-x^2} \right)$

$\displaystyle \frac{d^2 A}{dx^2} = 2 \frac{d}{dx} (e^{-x^2}) - 4 \frac{d}{dx} (x^2 e^{-x^2})$

$\displaystyle \frac{d^2 A}{dx^2} = 2(-2x e^{-x^2}) - 4(2xe^{-x^2} - 2x^3 e^{-x^2})$

$\displaystyle \frac{d^2 A}{dx^2} = -4xe^{-x^2} - 8xe^{-x^2} + 8x^3 e^{-x^2}$

$\displaystyle \frac{d^2 A}{dx^2} = -12x e^{-x^2} + 8x^3 e^{-x^2}$

Sustituyendo el valor de “ $x$ ” en el resultado de la segunda derivada

$\displaystyle \left. \frac{d^2 A}{dx^2} \right|_{x=\frac{1}{\sqrt{2}}} = -12 \left[\frac{1}{\sqrt{2}} e^{- \left( \frac{1}{\sqrt{2}} \right)^2} \right] + 8 \left( \frac{1}{\sqrt{2}} \right)^3 e^{- \left(\frac{1}{\sqrt{2}} \right)^2}$

$\displaystyle \frac{d^2 A}{dx^2} = -3.4311$

Como $\displaystyle \frac{d^2 A}{dx^2} < 0$ se trata de un máximo. El valor calculado del área del rectángulo es máximo.

Paso 7. Ahora se calculan los puntos de inflexión. Para ello, se toma la ecuación de la curva y se determina hasta su segunda derivada

$y = e^{-x^2}$

$\displaystyle \frac{d}{dx} (y) = \frac{d}{dx} (e^{-x^2})$

$\displaystyle \frac{dy}{dx} = -2xe^{-x^2}$

$\displaystyle \frac{d}{dx} \left( \frac{dy}{dx} \right) = \frac{d}{dx} (-2x e^{-x^2})$

$\displaystyle \frac{d^2 y}{dx^2} = -2e^{-x^2} + 4x^2 e^{-x^2}$

Los puntos de inflexión se cumplen cuando la segunda derivada es nula. Entonces, con $\displaystyle \frac{d^2 y}{dx^2} = 0$ , se tiene los siguiente

$\displaystyle \frac{d^2 y}{dx^2} = -2e^{-x^2} + 4x^2 e^{-x^2}$

$\displaystyle 0 = -2e^{-x^2} + 4x^2 e^{-x^2}$

$2e^{-x^2} = 4x^2 e^{-x^2}$

$1 = 2x^2$

$\displaystyle x = \pm \frac{1}{\sqrt{2}} = \pm \frac{\sqrt{2}}{2}$

Sustituyendo el valor de “ $x$ ” en la ecuación de la curva

$\displaystyle y = e^{- \left( \pm \frac{1}{\sqrt{2}} \right)^2}$

$\displaystyle y = e^{-1/2} = \frac{1}{\sqrt{e}}$

$\displaystyle y = \frac{\sqrt{e}}{e}$

Por lo tanto, los vértices del rectángulo con área máxima están en los puntos de inflexión, $\displaystyle \left(\frac{2}{\sqrt{2}}, \frac{\sqrt{e}}{e} \right)$ y $\displaystyle \left(- \frac{2}{\sqrt{2}}, \frac{\sqrt{e}}{e} \right)$ , de la curva. El área máxima del rectángulo será de $\displaystyle \frac{\sqrt{2}e}{e} \approx 0.8578 \ (u^2)$ .