División de voltaje para dos resistencias o resistores. Circuitos eléctricos.

Introducción

El enfoque consistirá con un circuito simple. Este circuito consiste en una fuente de voltaje independiente que está en serie con dos resistores. Se ilustra un flujo de corriente que va en el sentido de las manecillas del reloj (sentido horario). Si este supuesto es correcto, la solución de las ecuaciones que terminan la corriente dará un valor positivo. Si la corriente fluye en realidad en sentido opuesto, el valor de la variable correspondiente simplemente es negativo, indicando que la dirección del flujo es contraria a la supuesta. También se observan las asignaciones de polaridad de voltaje para $v_{R_1}$ y $v_{R_2}$ .

Figura 1. Circuito para el desarrollo de la fórmula de la división de voltaje para 2 resistencias.

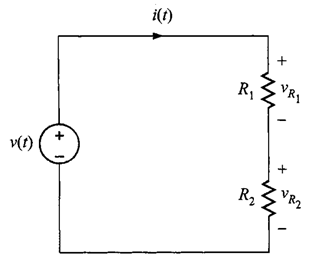
Al aplicar la ley de Kirchhoff de voltaje se obtiene

$\displaystyle \sum_{j=1}^{N}{v_j}=0$

$-v(t) + v_{R_1} + v_{R_2} = 0$

$v(t) = v_{R_1} + v_{R_2}$

Por la ley de Ohm se sabe que

$v_{R_1} = i(t) R_1$ y $v_{R_2} = i(t) R_2$

Entonces

$v(t) = i(t) R_1 + i(t) R_2$

$v(t) = (R_1+R_2 )i(t)$

Resolviendo la ecuación para $i(t)$

$\displaystyle i(t) = \frac{v(t)}{R_1+R_2}$

Una vez que se conoce la corriente, al aplicar la ley de Ohm se puede determinar el voltaje para cada resistor

$\displaystyle v_{R_1} = i(t) R_1 = \frac{v(t)}{R_1+R_2} R_1 = \frac{R_1}{R_1+R_2} v(t)$

$\displaystyle v_{R_2} = i(t) R_2 = \frac{v(t)}{R_1+R_2} R_2 = \frac{R_2}{R_1+R_2} v(t)$

Problema resuelto

Problema 1. Considere el circuito de la figura 2. Se tiene que $V_S=9 \ \text{V}$ , $R_1=90 \ \text{k} \Omega$ y $R_2 = 30 \ \text{k} \Omega$ .

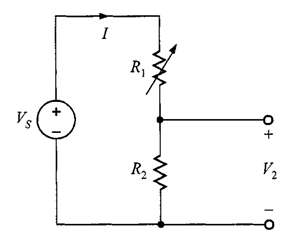
Examinar cuál es el cambio tanto en el voltaje en $R_2$ como en la potencia que absorbe dicho resistor cuando $R_1$ cambie de 90 kΩ a 15 kΩ.

Solución. Esto se trata de un circuito divisor de voltaje, el voltaje $V_2$ se puede obtener directamente como

$\displaystyle V_2 = \left( \frac{R_2}{R_1+R_2} \right) V_S$

$\displaystyle V_2 = \left( \frac{30 \ \text{k} \Omega}{90 \ \text{k} \Omega + 30 \ \text{k} \Omega} \right) (9 \ \text{V})$

$\displaystyle V_2 = \left( \frac{30 \times 10^3 \ \Omega}{90 \times 10^3 \ \Omega + 30 \times 10^3 \ \Omega} \right) (9 \ \text{V})$

$\therefore V_2 = 2.25 \ \text{V}$

Y determinando la potencia que absorbe el resistor $R_2$

$\displaystyle P_2 = I^2 R_2 = \left( \frac{V_S}{R_1+R_2} \right)^2 R_2$

$\displaystyle P_2 = {\left( \frac{9 \ \text{V}}{90 \ \text{k} \Omega + 30 \ \text{k} \Omega} \right)}^2 (30 \ \text{k} \Omega) = {\left( \frac{9 V}{90 \times 10^3 \ \Omega + 30 \times 10^3 \Omega} \right)}^2 (30 \times 10^3 \Omega)$

$\therefore P_2 = 0.169 \ \text{mW}$

Cuando $R_1 = 90 \ \text{k} \Omega$ , $R_2$ tiene tiene un voltaje de $V_2=2.25 \ \text{V}$ y con una potencia que absorbe de $P_2 = 0.169 \ \text{mW}$ .

Ahora, suponiendo que el resistor variable cambia de 90 kΩ a 15 kΩ, se tiene lo siguiente

$\displaystyle V_2 = \left( \frac{R_2}{R_1+R_2} \right) V_S$

$\displaystyle V_2 = \left( \frac{30 \ \text{k} \Omega}{15 \ \text{k} \Omega + 30 \ \text{k} \Omega} \right) (9 \ \text{V})$

$\displaystyle V_2 = \left( \frac{30 \times 10^3 \ \Omega}{15 \times 10^3 \ \Omega + 30 \times 10^3 \ \Omega} \right) (9 \ \text{V})$

$\therefore V_2 = 6 \ \text{V}$

Y la potencia absorbida por el resistor $R_2$ es

$\displaystyle P_2 = I^2 R_2 = {\left(\frac{V_S}{R_1+R_2} \right)}^2 R_2$

$\displaystyle P_2 = {\left( \frac{9 \ \text{V}}{15 \ \text{k} \Omega + 30 \ \text{k} \Omega }\right)}^2 (30 \ \text{k} \Omega) = {\left( \frac{9 \ \text{V}}{15 \times 10^3 \ \Omega + 30 \times 10^3 \ \Omega} \right)}^2 (30 \times 10^3 \ \Omega)$