Análisis de nodos para circuitos con fuentes de voltaje independientes. Circuitos eléctricos.

Problemas resueltos

Problema 1. Se considera el circuito de la figura 1. Determinar todos los voltajes de nodo y las corrientes de rama.

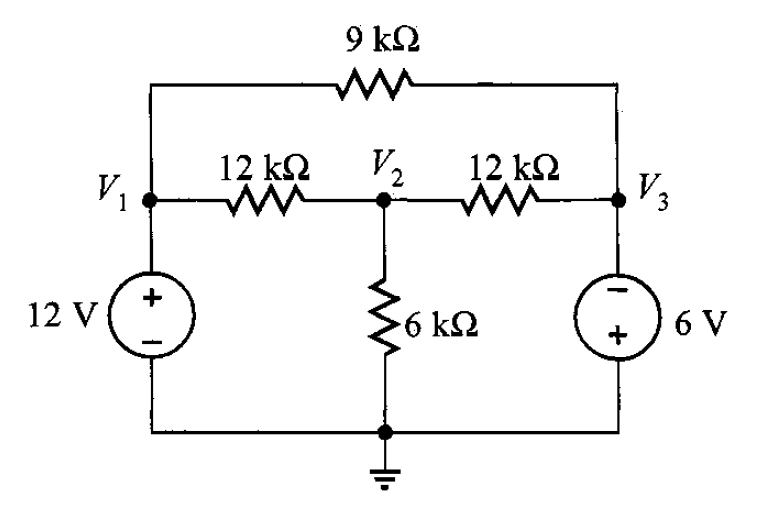
Solución. Esta red tiene tres nodos diferentes al de referencia con los voltajes de nodo $V_1$ , $V_2$ y $V_3$ . Para comenzar se debe utilizar la LKC para cada uno de los nodos que no son el de referencia a fin de hallar todos los voltajes de nodo. En este circuito hay cuatro nodos, de los cuales 3 son los voltajes a determinar; las ecuaciones resultantes son simultáneas linealmente independientes resultantes producirían los voltajes de nodos desconocidos. Sin embargo, se observa que $V_1$ y $V_3$ son magnitudes conocidas, ya que una fuente independiente conectada entre el nodo de referencia y cada uno de estos nodos. Los valores son $V_1 = 12 \ \text{V}$ y $V_3 = -6 \ \text{V}$ . Solo falta determinar el valor de $V_2$ . Para ello, utilizando LKC en el nodo central, resulta

$\displaystyle \sum_{j=1}^n{V_j} = 0$

$\displaystyle \frac{V_2 - V_1}{12 \ \text{k}} + \frac{V_2}{6 \ \text{k}} + \frac{V_2 - V_3}{12 \ \text{k}} = 0$

$\displaystyle \frac{V_2}{12 \ \text{k}} - \frac{V_1}{12 \ \text{k}} + \frac{V_2}{6 \ \text{k}} + \frac{V_2}{12 \ \text{k}} - \frac{V_3}{12 \ \text{k}} = 0$

$\displaystyle - \left(\frac{1}{12 \ \text{k}} \right) V_1 + \left(\frac{1}{12 \ \text{k}} + \frac{1}{6 \ \text{k}} + \frac{1}{12 \ \text{k}} \right) V_2 - \left(\frac{1}{12 \ \text{k}} \right) V_3 = 0$

$\displaystyle - \left(\frac{1}{12 \ \text{k}} \right) V_1 + \left(\frac{1}{3 \ \text{k}} \right) V_2 - \left(\frac{1}{12 \ \text{k}} \right) V_3 = 0$

Recordando que $V_1 = 12 \ \text{V}$ y $V_3 = -6 \ \text{V}$

$\displaystyle - \left(\frac{1}{12 \ \text{k}} \right) (12) + \left(\frac{1}{3 \ \text{k}} \right) V_2 - \left(\frac{1}{12 \ \text{k}} \right) (-6) = 0$

$\displaystyle - \frac{1}{1 \ \text{k}} + \left(\frac{1}{3 \ \text{k}} \right) V_2 + \frac{1}{2 \ \text{k}} = 0$

$\displaystyle \left(\frac{1}{3 \ \text{k}} \right) V_2 - \frac{1}{2 \ \text{k}} = 0$

$\displaystyle V_2 = \frac{3}{2} \ \text{V}$

Figura 2. Señalando el nodo central para el análisis de LKC.

Una vez determinado los voltajes de cada nodo, se puede determinar las corriente de rama. La primer corriente que circula por el resistor de $12 \ \text{k}$ es

$\displaystyle I_1 = \frac{V_1 - V_2}{12 \ \text{k}}$

$\displaystyle I_1 = \frac{12 - \frac{3}{2}}{12 \ \text{k}} = \frac{\frac{21}{2}}{12 \ \times 10^{3}} = \frac{21}{24} \ \times 10^{-3} = \frac{7}{8} \ \times 10^{-3}$

$\displaystyle \therefore I_1 = \frac{7}{8} \ \text{mA}$

La corriente $I_2$ que pasa por el resistor de $9 \ \text{k} \Omega$ es

$\displaystyle I_2 = \frac{V_1 - V_3}{9 \ \text{k}}$

$\displaystyle I_2 = \frac{12 - (-6)}{9 \ \text{k}} = \frac{12 + 6}{9 \ \times 10^{3}} = 2 \times 10^{-3}$

$\displaystyle \therefore I_2 = 2 \ \text{mA}$

que va de izquierda a derecha. Y en la corriente $I_3$ que circula por el segundo resistor $12 \ \text{k} \Omega$ (entre $V_2$ y $V_3$ )

$\displaystyle I_3 = \frac{V_2 - V_3}{12 \ \text{k}}$

$\displaystyle I_3 = \frac{\frac{3}{2} - (-6)}{12 \ \text{k}} = \frac{\frac{3}{2} + 6}{12 \ \text{k}} = \frac{\frac{15}{2}}{12 \ \times 10^{3}} = \frac{15}{24} \ \times 10^{-3} = \frac{5}{8} \ \times 10^{-3}$

$\displaystyle \therefore I_3 = \ \frac{5}{8} \text{mA}$

La corriente $I_4$ que circula por el resistor $6 \ \text{k} \Omega$ es

$\displaystyle I_4 = \frac{V_2}{6 \ \text{k}}$

$\displaystyle I_4 = \frac{\frac{3}{2}}{6 \ \text{k}} = \frac{\frac{3}{2}}{6 \times 10^{3}} = \frac{3}{12 \times 10^3} = \frac{1}{4} \times 10^{-3}$

$\displaystyle \therefore I_4 = \frac{1}{4} \ \text{mA}$

Todos los resultados obtenidos durante la solución del problema 1, se visualizan en la figura 3.

Figura 3. Circuito del problema 1 que muestra todos los voltajes de cada nodo y las corrientes de rama.

Problema 2. Se desea encontrar las corrientes en los dos resistores del circuito de la figura 4.

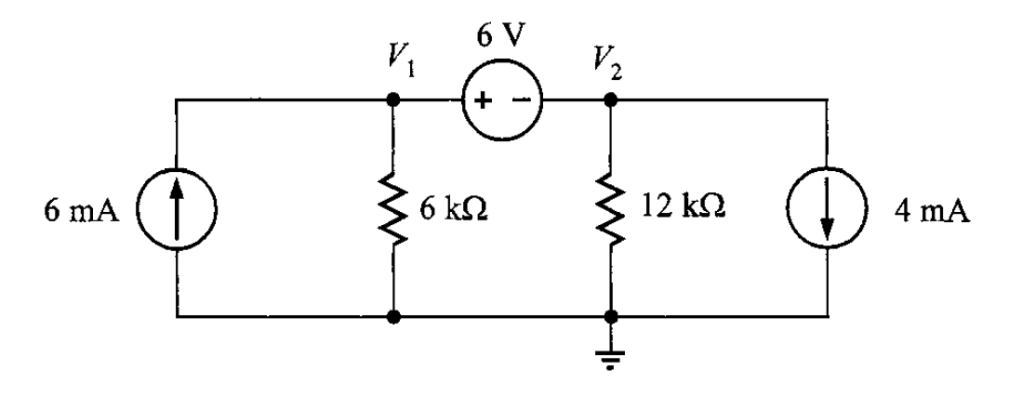
Solución. La corriente de rama que pasa por la fuente de 6 V es desconocida, y no puede expresarse directamente usando la ley de Ohm. Es posible asignarle una literal a esta corriente y escribir las ecuaciones de la LKC para los dos nodos distintos al de referencia en términos de esta corriente. No obstante, esto no sería una solución definitiva ya que esta técnica produce dos ecuaciones simultáneas linealmente independientes en términos de tres incógnitas; esto es, los dos voltajes de nodo y la corriente en la fuente de corriente.

Para resolver este dilema, se recuerda que en un circuito de $N$ nodos se requieren $N-1$ ecuaciones linealmente independientes para determinar $N-1$ voltajes de nodos distintos al de referencia. Se necesitas dos ecuaciones linealmente independientes ya que la red tiene tres nodos.

Entonces, la diferencia de potencias entres los dos nodos está restringida por la fuente de voltajes

$\displaystyle V_1 - V_2 = 6$

Esta ecuación de restricción es una de las dos ecuaciones linealmente independientes requeridas para determinar los voltajes de nodo.

Figura 5. Indicando los nodos V1 y V2 entre la fuente de voltaje de 6V.

La segunda ecuación se determina utilizando LKC a dicha superficie , la cual se denomina comúnmente supernodo. Entonces

$\displaystyle \sum_{j=1}^{n}{I_j} = 0$

$\displaystyle -6 \ \text{m} + I_1 + I_2 + 4 \ \text{m} = 0$

$\displaystyle I_1 + I_2 - 2 \ \text{m} = 0$

$\displaystyle I_1 + I_2 = 2 \ \text{m}$

Observando en la figura 5, se tiene que $\displaystyle I_1 = \frac{V_1}{6 \ \text{k}}$ y $\displaystyle I_2 = \frac{V_2}{12 \ \text{k}}$ , resulta que

$\displaystyle \frac{V_1}{6 \ \text{k}} + \frac{V_2}{12 \ \text{k}} = 2 \ \text{m}$

$\displaystyle \left(\frac{1}{6 \ \text{k}} \right) V_1 + \left(\frac{1}{12 \ \text{k}} \right) V_2 = 2 \ \text{m}$

Las ecuaciones son

\displaystyle \left(\frac{1}{6 \ \text{k}} \right) V_1 + \left(\frac{1}{12 \ \text{k}} \right) V_2 = 2 \ \text{m}

Expresándolo en forma matricial

$\displaystyle \left[\begin{matrix} 1 & -1 \\ \frac{1}{6 \ \text{k}} & \frac{1}{12 \ \text{k}} \end{matrix} \right] \left[\begin{matrix} V_1 \\ V_2 \end{matrix} \right] = \left[\begin{matrix} 6 \\ 2 \ \text{m} \end{matrix} \right]$

$\displaystyle \bold{H} \bold{V} = \bold{F}$

donde $\bold{H}$ representa los valores de los coeficientes que acompañan a cada voltaje de nodo y $\bold{F}$ representa los valores de cada ecuación del sistema.

Despejando $\bold{V}$

$\displaystyle \bold{V} = \bold{H}^{-1} \bold{F}$

La matriz del segundo miembro debe calcularse su inversa; primero se termina su determinante y después su matriz adjunta traspuesta. La determinante es

$\displaystyle \text{det} \ \bold{H} = \left|\begin{matrix} 1 & -1 \\ \frac{1}{6 \ \text{k}} & \frac{1}{12 \ \text{k}} \end{matrix} \right|$

$\displaystyle \text{det} \ \bold{H} = (1) \left( \frac{1}{12 \ \text{k}} \right) - (-1) \left( \frac{1}{6 \ \text{k}} \right)$

$\displaystyle \text{det} \ \bold{H} = \left( \frac{1}{12 \ \text{k}} \right) - \left( - \frac{1}{6 \ \text{k}} \right) = \frac{1}{12 \ \text{k}} + \frac{1}{6 \ \text{k}} = \frac{3}{12 \ \text{k}}$

$\displaystyle \text{det} \ \bold{H} = \frac{1}{4 \ \text{k}}$

La matriz adjunta es determinada por los cofactores y los menores. Entonces

\displaystyle C_{11} = {(-1)}^{1+1} \left(\frac{1}{12 \ \text{k}} \right) = \frac{1}{12 \ \text{k}}

\displaystyle C_{12} = {(-1)}^{1+2} \left(\frac{1}{6 \ \text{k}} \right) = - \frac{1}{6 \ \text{k}}

Después

$\displaystyle Adj \ \bold{H} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right] = \left[\begin{matrix} \frac{1}{12 \ \text{k}} &- \frac{1}{6 \ \text{k}} \\ 1 & 1 \end{matrix} \right]$

Y la matriz adjunta traspuesta es

$\displaystyle {(Adj \ \bold{H})}^T = \left[\begin{matrix} \frac{1}{12 \ \text{k}} & 1 \\ - \frac{1}{6 \ \text{k}} & 1 \end{matrix} \right]$

Calculando matriz inversa

$\displaystyle \bold{H}^{-1} = \frac{{\left(Adj \ \bold{H}\right)}^T}{\text{det} \ \bold{H}} = \left(\frac{1}{\text{det} \ \bold{H}} \right) {\left(Adj \ \bold{H}\right)}^T$

$\displaystyle \bold{H}^{-1} = \left(\frac{1}{\frac{1}{4 \ \text{k}}} \right) \left[\begin{matrix} \frac{1}{12 \ \text{k}} & 1 \\ - \frac{1}{6 \ \text{k}} & 1 \end{matrix} \right] = \left(4 \ \text{k} \right) \left[\begin{matrix} \frac{1}{12 \ \text{k}} & 1 \\ - \frac{1}{6 \ \text{k}} & 1 \end{matrix} \right]$

$\displaystyle \bold{H}^{-1} = \left[\begin{matrix} \frac{1}{12 \ \text{k}}\left(4 \ \text{k} \right) & 1 \left(4 \ \text{k} \right) \\ - \frac{1}{6 \ \text{k}} \left(4 \ \text{k} \right) & 1 \left(4 \ \text{k} \right) \end{matrix} \right] = \left[\begin{matrix} \frac{4}{12} & 4 \ \text{k} \\ - \frac{4}{6} & 4 \ \text{k} \end{matrix} \right]$

$\displaystyle \bold{H}^{-1} = \left[\begin{matrix} \frac{1}{3} & 4 \ \text{k} \\ - \frac{2}{3} & 4 \ \text{k} \end{matrix} \right]$

Regresando a la forma matricial

$\displaystyle \bold{V} = \bold{H}^{-1} \bold{F}$

$\displaystyle \bold{V} = \left[\begin{matrix} \frac{1}{3} & 4 \ \text{k} \\ - \frac{2}{3} & 4 \ \text{k} \end{matrix} \right] \left[\begin{matrix} 6 \\ 2 \ \text{m} \end{matrix} \right]$

Realizando la multiplicación matricial (sin olvidar que $\text{k} = 1 \times 10^{3}$ y $\text{m} = 1 \times 10^{-3}$ ), resulta

$\displaystyle \bold{V} = \left[\begin{matrix} \frac{1}{3} & 4 \times 10^{3} \\ - \frac{2}{3} & 4 \times 10^{3} \end{matrix} \right] \left[\begin{matrix} 6 \\ 2 \times 10^{-3} \end{matrix} \right]$

$\displaystyle \bold{V} = \left[\begin{matrix} \left(\frac{1}{3} \right)(6) + \left(4 \times 10^{3} \right) \left(2 \times 10^{-3} \right) \\ \left(- \frac{2}{3} \right)(6) + (4 \times 10^{3}) \left(2 \times 10^{-3} \right) \end{matrix} \right] = \left[\begin{matrix} 2 + 8 \\ -4 + 8 \end{matrix} \right]$

$\displaystyle \therefore \bold{V} = \left[\begin{matrix} 10 \\ 4 \end{matrix} \right]$

Así que $V_1 = 10 \ \text{V}$ y $V_2 = 4 \ \text{V}$ . Ahora solo falta calcular las corrientes de rama. La corriente $I_1$ que circula por el resistor de $6 \ \text{k}$ es

$\displaystyle I_1 = \frac{V_1}{6 \ \text{k}}$

$\displaystyle I_1 = \frac{10}{6 \times 10^3} = \frac{10}{6} \times 10^{-3} = \frac{5}{3} \times 10^{-3}$

$\displaystyle \therefore I_1 = \frac{5}{3} \ \text{mA}$

Y la corriente $I_2$ que circula por el resistor de $12 \ \text{k}$ es

$\displaystyle I_2 = \frac{V_2}{12 \ \text{k}}$

$\displaystyle I_2 = \frac{4}{12 \times 10^3} = \frac{4}{12} \times 10^{-3} = \frac{1}{3} \times 10^{-3}$

$\displaystyle \therefore I_2 = \frac{1}{3} \ \text{mA}$

Problema 3. Determine la corriente $I_o$ en la red de la figura 6.

Solución. Al analizar la red se observa que se conocen los voltajes de nodo $V_2$ y $V_3$ , y que los voltaje de nodo $V_1$ y $V_3$ están restringidos por la ecuación

$\displaystyle V_1 - V_3 = 12$

que al despejar $V_1$

$\displaystyle V_1 = V_3 + 12$

En la figura 7 se muestra nuevamente la red pero indicando el supernodo.

Figura 7. Circuito del problema 3 indicando el supernodo.

Para encontrar $I_o$ , es necesario hallar $V_3$ y para ello sólo basta con usar la LKC en el supernodo (mostrado en la figura 7). Entonces

$\displaystyle \sum_{j=1}^n{I_j} = 0$

$\displaystyle \frac{V_1 - (-6)}{2 \ \text{k}} + \frac{V_3 - (-6)}{1 \ \text{k}} + \frac{V_3}{2 \ \text{k}} + \frac{V_3 - 12}{1 \ \text{k}} + \frac{V_1 - 12}{2 \ \text{k}} = 0$

$\displaystyle \frac{V_1 + 6}{2 \ \text{k}} + \frac{V_3 + 6}{1 \ \text{k}} + \frac{V_3}{2 \ \text{k}} + \frac{V_3 - 12}{1 \ \text{k}} + \frac{V_1 - 12}{2 \ \text{k}} = 0$

Recordando que $\displaystyle V_1 = V_3 + 12$

$\displaystyle \frac{V_3 + 12 + 6}{2 \ \text{k}} + \frac{V_3 + 6}{1 \ \text{k}} + \frac{V_3}{2 \ \text{k}} + \frac{V_3 - 12}{1 \ \text{k}} + \frac{V_3 + 12 - 12}{2 \ \text{k}} = 0$

$\displaystyle \frac{V_3 + 18}{2 \ \text{k}} + \frac{V_3 + 6}{1 \ \text{k}} + \frac{V_3}{2 \ \text{k}} + \frac{V_3 - 12}{1 \ \text{k}} + \frac{V_3}{2 \ \text{k}} = 0$

$\displaystyle \left(\frac{1}{2 \ \text{k}} + \frac{1}{1 \ \text{k}} + \frac{1}{2 \ \text{k}} + \frac{1}{1 \ \text{k}} + \frac{1}{2 \ \text{k}} \right) V_3 + \frac{18}{2 \ \text{k}} + \frac{6}{1 \ \text{k}} - \frac{12}{1 \ \text{k}} = 0$

$\displaystyle \left(\frac{1}{2 \ \text{k}} + \frac{1}{1 \ \text{k}} + \frac{1}{2 \ \text{k}} + \frac{1}{1 \ \text{k}} + \frac{1}{2 \ \text{k}} \right) V_3 + \frac{9}{1 \ \text{k}} + \frac{6}{1 \ \text{k}} - \frac{12}{1 \ \text{k}} = 0$

$\displaystyle \left(\frac{7}{2 \ \text{k}} \right) V_3 + \frac{3}{1 \ \text{k}} = 0$

$\displaystyle V_3 = - \frac{6}{7} \ \text{V}$

Una vez calculado el valor de $V_3$ , por ley de Ohm, se despeja $I_o$ , se sustituye y se obtiene el resultado final

$\displaystyle V_3 = (2 \ \text{k}) I_o$

$\displaystyle I_o = \frac{V_3}{2 \ \text{k}} = \frac{- \frac{6}{7}}{2 \ \text{k}} = \frac{- \frac{6}{7}}{2 \times 10^3} = -\frac{6}{14} \times 10^{-3}$

$\displaystyle \therefore I_o = -\frac{3}{7} \ \text{mA}$

$\displaystyle C_{11} = {(-1)}^{1+1} \left(\frac{1}{12 \ \text{k}} \right) = \frac{1}{12 \ \text{k}}$	$\displaystyle C_{12} = {(-1)}^{1+2} \left(\frac{1}{6 \ \text{k}} \right) = - \frac{1}{6 \ \text{k}}$
$\displaystyle C_{21} = {(-1)}^{2+1} \left(- 1 \right) = 1$	$\displaystyle C_{22} = {(-1)}^{2+2} \left(1 \right) = 1$

Análisis de nodos para circuitos con fuentes de voltaje independientes. Circuitos eléctricos.

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Análisis de nodos para circuitos con fuentes de voltaje independientes. Circuitos eléctricos.

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta