Análisis de lazos para circuitos con fuentes dependientes. Circuitos eléctricos.

Problemas resueltos

Problema 1. Encontrar $V_o$ en el circuito de la figura 1, el cual contiene una fuente de voltaje controlada por voltaje.

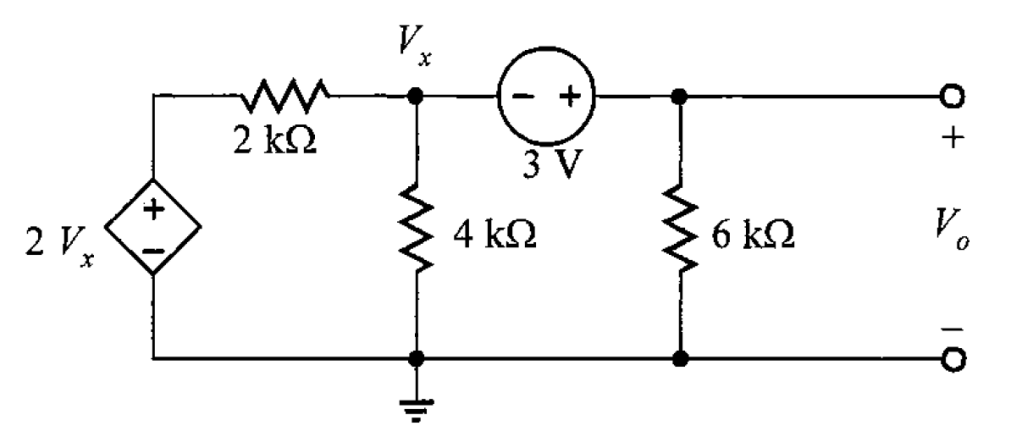
Solución. Se indican los lazos en el circuito para poder aplicar la LKV.

Figura 2. Señalando los lazos en el circuito del problema 1.

Después, del primer lazo, al aplicar LKV, su ecuación es

$\displaystyle \sum_{j=1}^n{V_j}=0$

$\displaystyle - 2V_x + (2 \ \text{k})(I_1 + I_2) + (4 \ \text{k}) I_2 = 0$

$\displaystyle - 2V_x + (2 \ \text{k})I_1 + (2 \ \text{k}) I_2 + (4 \ \text{k}) I_2 = 0$

$\displaystyle (6 \ \text{k})I_1 + (2 \ \text{k}) I_2 = 2 V_x$

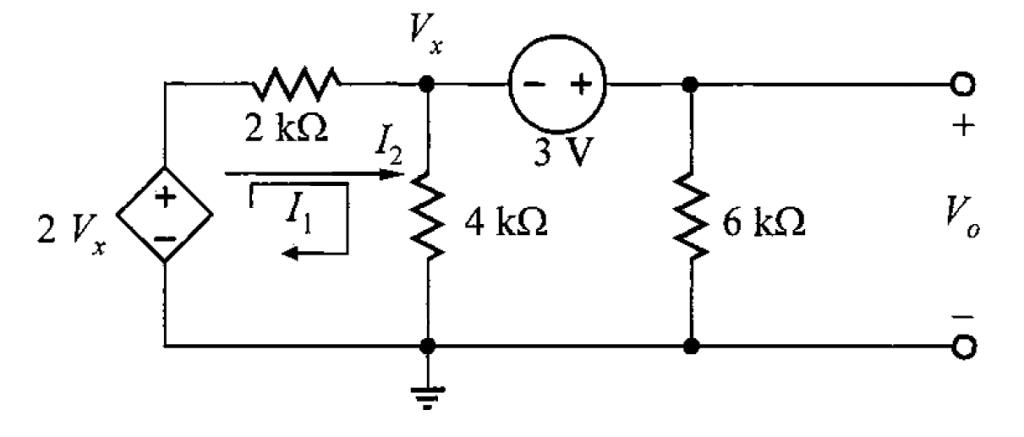
Y del segundo lazo, al aplicar LKV, su ecuación es

$\displaystyle \sum_{j=1}^n{V_j}=0$

$\displaystyle - 2V_x + (2 \ \text{k})(I_1 + I_2) - 3 + (6 \ \text{k}) I_2 = 0$

$\displaystyle - 2V_x + (2 \ \text{k}) I_1 + (2 \ \text{k}) I_2 - 3 + (6 \ \text{k}) I_2 = 0$

$\displaystyle (2 \ \text{k}) I_1 + (8 \ \text{k}) I_2 = 3 + 2V_x$

Tomando las ecuaciones obtenidas en cada lazo, se tiene el siguiente sistema

\displaystyle (6 \ \text{k})I_1 + (2 \ \text{k}) I_2 = 2 V_x

\displaystyle (2 \ \text{k}) I_1 + (8 \ \text{k}) I_2 = 3 + 2V_x

La ecuación de restricción es $V_x = (4 \ \text{k}) I_1$ . Sustituyendo en el sistema de ecuaciones resulta que

\displaystyle (6 \ \text{k})I_1 + (2 \ \text{k}) I_2 = 2 (4 \ \text{k}) I_1

\displaystyle (2 \ \text{k}) I_1 + (8 \ \text{k}) I_2 = 3 + 2(4 \ \text{k}) I_1

Simplificando

\displaystyle - (2 \ \text{k})I_1 + (2 \ \text{k}) I_2 = 0

\displaystyle - (6 \ \text{k}) I_1 + (8 \ \text{k}) I_2 = 3

Expresándolo en forma matricial

$\displaystyle \left[\begin{matrix} -2 \ \text{k} & 2 \ \text{k}\\ -6 \ \text{k} & 8\ \text{k} \end{matrix} \right] \left[\begin{matrix} I_1 \\ I_2 \end{matrix} \right] = \left[\begin{matrix} 0 \\ 3 \end{matrix} \right]$

Donde su forma general es

$\displaystyle \bold{R} \bold{I} = \bold{V}$

Despejando $\bold{I}$ , se tiene que

$\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}$

Por lo que es necesario determinar la matriz inversa de $\bold{R}$ . Calculando su determinante, resulta

$\displaystyle \text{det} \ \bold{R} = \left|\begin{matrix} -2 \ \text{k} & 2 \ \text{k}\\ -6 \ \text{k} & 8\ \text{k} \end{matrix} \right|$

$\displaystyle \text{det} \ \bold{R} = (- 16 \ \text{k}^2 ) - (-12 \ \text{k}^2)$

$\displaystyle \text{det} \ \bold{R} = - 4 \ \text{k}^2$

La matriz adjunta de $\bold{B}$ es

$\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right]$

\displaystyle C_{11} = {(-1)}^{1+1} \left(8 \ \text{k} \right) = 8 \ \text{k}

\displaystyle C_{12} = {(-1)}^{1+2} \left(- 6 \ \text{k} \right) = 6 \ \text{k}

así que

$\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right]$

$\displaystyle Adj \ \bold{R} = \left[\begin{matrix} 8 \ \text{k} & 6 \ \text{k} \\ -2 \ \text{k} & -2 \ \text{k} \end{matrix} \right]$

y la traspuesta de la matriz adjunta de $\bold{R}$ es

$\displaystyle {\left(Adj \ \bold{R}\right)}^T = \left[\begin{matrix} 8 \ \text{k} & -2 \ \text{k} \\ 6 \ \text{k} & -2 \ \text{k} \end{matrix} \right]$

Entonces, la inversa de $\bold{R}^{-1}$ es

$\displaystyle \bold{R}^{-1} = \frac{{\left(Adj \ \bold{R}\right)}^T}{\text{det} \ \bold{R}} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {\left(Adj \ \bold{R}\right)}^T$

$\displaystyle \bold{R}^{-1} = \left(\frac{1}{-4 \ \text{k}^2} \right) \left[\begin{matrix} 8 \ \text{k} & -2 \ \text{k} \\ 6 \ \text{k} & -2 \ \text{k} \end{matrix} \right]$

$\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \left(\frac{1}{-4 \ \text{k}^2} \right)(8 \ \text{k}) & \left(\frac{1}{-4 \ \text{k}^2} \right)(-2 \ \text{k}) \\ \\ \left(\frac{1}{-4 \ \text{k}^2} \right)(6 \ \text{k}) & \left(\frac{1}{-4 \ \text{k}^2} \right)(-2 \ \text{k}) \end{matrix} \right]$

$\displaystyle \bold{R}^{-1} = \left[\begin{matrix} - \frac{8}{4 \ \text{k}} & \frac{2}{4 \ \text{k}} \\ \\ - \frac{6}{4 \ \text{k}} & \frac{2}{4 \ \text{k}} \end{matrix} \right]$

$\displaystyle \bold{R}^{-1} = \left[\begin{matrix} - \frac{2}{1 \ \text{k}} & \frac{1}{2 \ \text{k}} \\ \\ - \frac{3}{2 \ \text{k}} & \frac{1}{2 \ \text{k}} \end{matrix} \right] = \left[\begin{matrix} - \frac{2}{1 \times 10^3} & \frac{1}{2 \times 10^3} \\ \\ - \frac{3}{2 \times 10^3} & \frac{1}{2 \times 10^3} \end{matrix} \right]$

$\displaystyle \bold{R}^{-1} = \left[\begin{matrix} - 2 \times 10^{-3} & \frac{1}{2} \times 10^{-3} \\ \\ - \frac{3}{2} \times 10^{-3} & \frac{1}{2} \times 10^{-3} \end{matrix} \right]$

Regresando al despeje de $\bold{I}$

$\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}$

$\displaystyle \left[\begin{matrix} I_1 \\ I_2 \end{matrix} \right] = \left[\begin{matrix} - 2 \times 10^{-3} & \frac{1}{2} \times 10^{-3} \\ \\ - \frac{3}{2} \times 10^{-3} & \frac{1}{2} \times 10^{-3} \end{matrix} \right] \left[\begin{matrix} 0 \\ 3 \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} I_1 \\ I_2 \end{matrix} \right] = \left[\begin{matrix} \left(- 2 \times 10^{-3} \right)(0) + \left(\frac{1}{2} \times 10^{-3} \right)(3) \\ \\ \left(- \frac{3}{2} \times 10^{-3} \right)(0) + \left(\frac{1}{2} \times 10^{-3} \right)(3) \end{matrix} \right] = \left[\begin{matrix} 0 + \frac{3}{2} \times 10^{-3} \\ \\ 0 + \frac{3}{2} \times 10^{-3} \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} I_1 \\ I_2 \end{matrix} \right] = \left[\begin{matrix} \frac{3}{2} \times 10^{-3} \\ \\ \frac{3}{2} \times 10^{-3} \end{matrix} \right] = \left[\begin{matrix} \frac{3}{2} \\ \\ \frac{3}{2} \end{matrix} \right] \times 10^{-3}$

$\displaystyle \left[\begin{matrix} I_1 \\ I_2 \end{matrix} \right] = \left[\begin{matrix} \frac{3}{2} \\ \\ \frac{3}{2} \end{matrix} \right] \ \text{mA}$

Por lo que las corrientes halladas son $\displaystyle I_1 = \frac{3}{2} \ \text{mA}$ y $\displaystyle I_2 = \frac{3}{2} \ \text{mA}$ . El valor de $V_o$ es

$\displaystyle V_o = (6 \ \text{k}) I_2$

$\displaystyle V_o = (6 \ \text{k}) \left(\frac{3}{2} \ \text{m} \right) = (6 \times 10^3) \left(\frac{3}{2} \times 10^{-3} \right) = 9$

$\displaystyle \therefore V_o = 9 \ \text{V}$

Problema 2. Encontrar el valor de $V_o$ en el circuito de la figura 5, el cual contiene una fuente de corriente controlada por voltaje.

Solución. Se identifican las corrientes de malla en el circuito dado.

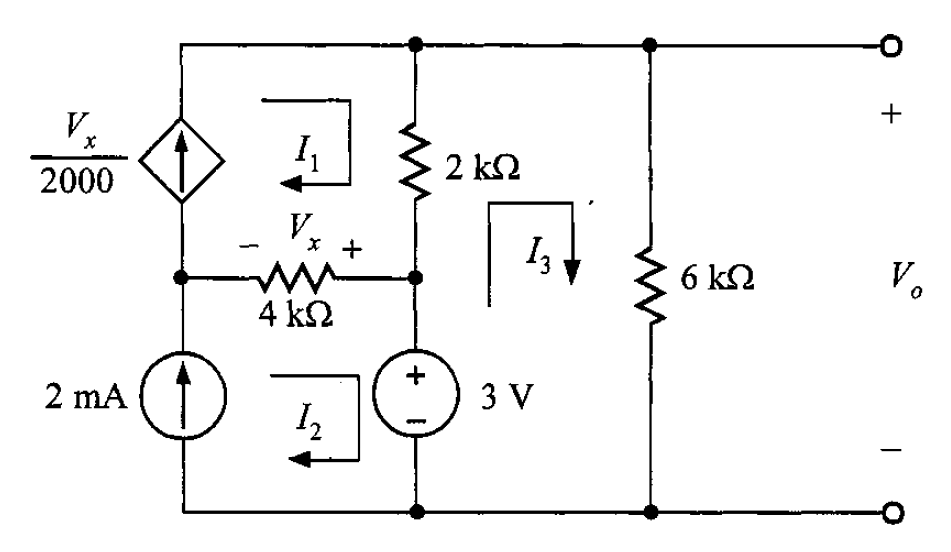
Figura 6. Identificando las corrientes de malla.

Se observa que las corrientes $I_1$ e $I_2$ son conducidas a través de las fuentes de corriente. Así que, las dos ecuaciones son

\displaystyle I_2 = 2 \ \text{mA} = 2 \times 10^{-3}

Ahora, en el caso de la tercera malla, al aplicar LKV su ecuación es

$\displaystyle \sum_{j=1}^n{V_j} = 0$

$\displaystyle -3 + (2 \ \text{k})(I_3 - I_1) + (6 \ \text{k})I_3 = 0$

$\displaystyle -3 + (2 \ \text{k})I_3 - (2 \ \text{k}) I_1 + (6 \ \text{k})I_3 = 0$

$\displaystyle - (2 \ \text{k}) I_1 + (8 \ \text{k})I_3 = 3$

Recordando que $\displaystyle I_1 = \frac{V_x}{2000}$ , resulta

$\displaystyle - (2 \ \text{k}) \frac{V_x}{2000} + (8 \ \text{k})I_3 = 3$

$\displaystyle - \frac{2 \times 10^3 V_x}{2000} + (8 \ \text{k})I_3 = 3$

$\displaystyle - \frac{2000 V_x}{2000} + (8 \ \text{k})I_3 = 3$

$\displaystyle -V_x + (8 \ \text{k})I_3 = 3$

En la figura 5, se observa que $V_{x} = (4 \ \text{k})(I_1 - I_2)$ . Aplicándolo en la expresión de $I_1$ , se tiene lo siguiente

$\displaystyle V_{x} = (4 \ \text{k})(I_1 - I_2)$

$\displaystyle V_{x} = (4 \ \text{k}) \left(\frac{V_x}{2000} - 2 \times 10^{-3} \right)$

$\displaystyle V_{x} = (4 \ \text{k}) \left(\frac{V_x}{2000} \right) - (4 \ \text{k}) (2 \times 10^{-3})$

$\displaystyle V_{x} = \left(\frac{4 \ \text{k}}{2000} \right) V_x - (4 \ \text{k})(2 \times 10^{-3})$

$\displaystyle V_{x} = \left(\frac{4 \times 10^3}{2 \times 10^3} \right) V_x - (4 \times 10^{3}) (2 \times 10^{-3})$

$\displaystyle V_{x} = 2 V_x - 8$

$\displaystyle V_{x} = 8 \ \text{V}$

Sustituyendo en la ecuación anterior

$\displaystyle -V_x + (8 \ \text{k})I_3 = 3$

$\displaystyle - 8 + (8 \ \text{k})I_3 = 3$

$\displaystyle (8 \ \text{k})I_3 = 11$

$\displaystyle I_3 = \frac{11}{8 \ \text{k}} = \frac{11}{8 \ \times 10^3} = \frac{11}{8} \times 10^{-3}$

$\displaystyle I_3 = \frac{11}{8} \ \text{mA}$

Finalmente, el voltaje $V_o$ es

$\displaystyle V_o = (6 \ \text{k}) I_3$

$\displaystyle V_o = (6 \ \text{k}) \left(\frac{11}{8} \ \text{m} \right) = (6 \times 10^3) \left(\frac{11}{8} \times 10^{-3} \right) = \frac{66}{8}$

$\displaystyle \therefore V_o = \frac{33}{4} \ \text{V}$

Problema 3. La red de la figura 8 contiene tanto una fuente de voltaje controlada por corriente como una fuente de corriente controlada por voltaje. Determinar las corrientes de lazo.

Solución. Se localizan las corrientes de lazo (figura 9).

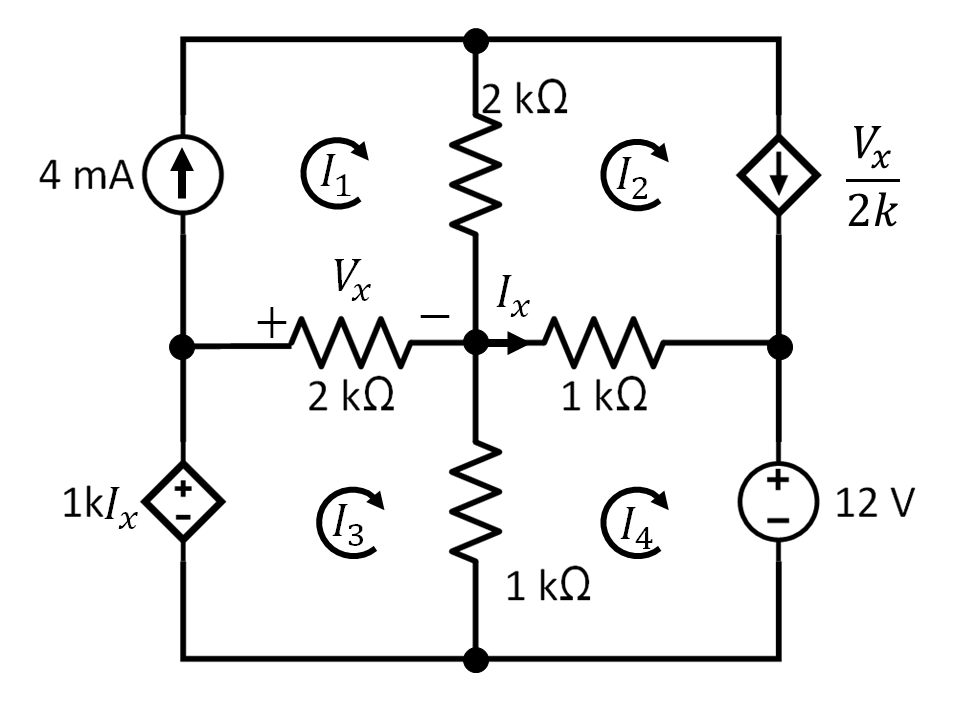
Figura 9. Localizando las corrientes de malla.

Se observa que hay dos ecuaciones de restricción y son

$\displaystyle V_{x} = (2 \ \text{k}) (I_3 - I_1)$

$\displaystyle I_x = I_4 - I_2$

Después, la corriente en la primera malla es

$I_1 = 4 \ \text{mA} = 4 \times 10^{-3}$

que por el momento, es conveniente expresarlo de esta manera

$\displaystyle I_1 = \frac{4}{1 \times 10^{3}} = \frac{4}{\text{k}}$

La corriente que conduce en la segunda malla es

$\displaystyle I_2 = \frac{V_x}{2 \ \text{k}} = \frac{V_x}{2} \times 10^{-3}$

que realizando un acomodo y sustitución de términos, resulta

$\displaystyle I_2 = \frac{(2 \ \text{k}) (I_3 - I_1)}{2 \ \text{k}}$

$\displaystyle I_2 = I_3 - I_1$

$\displaystyle I_1 + I_2 - I_3 = 0$

En la tercera malla solo se puede expresar una ecuación aplicando la LKV.

$\displaystyle \sum_{j=1}^n{V_j} = 0$

$\displaystyle -(1 \ \text{k}) I_x + (2 \ \text{k})(I_3 - I_1) + (1 \ \text{k})(I_3 - I_4) = 0$

$\displaystyle -(1 \ \text{k}) (I_4 - I_2) + (2 \ \text{k})(I_3 - I_1) + (1 \ \text{k})(I_3 - I_4) = 0$

$\displaystyle - (1 \ \text{k}) I_4 + (1 \ \text{k}) I_2 + (2 \ \text{k}) I_3 - (2 \ \text{k}) I_1 + (1 \ \text{k}) I_3 - (1 \ \text{k}) I_4 = 0$

$\displaystyle - (2 \ \text{k}) I_1 + (1 \ \text{k}) I_2 + (3 \ \text{k}) I_3 - (2 \ \text{k}) I_4 = 0$

$\displaystyle - (2 \ \text{k}) (4 \ \text{m})+ (1 \ \text{k}) I_2 + (3 \ \text{k}) I_3 - (2 \ \text{k}) I_4 = 0$

$\displaystyle - (2 \times 10^3) (4 \times 10^{-3})+ (1 \ \text{k}) I_2 + (3 \ \text{k}) I_3 - (2 \ \text{k}) I_4 = 0$

$\displaystyle - 8 + (1 \ \text{k}) I_2 + (3 \ \text{k}) I_3 - (2 \ \text{k}) I_4 = 0$

$\displaystyle (1 \ \text{k}) I_2 + (3 \ \text{k}) I_3 - (2 \ \text{k}) I_4 = 8$

Figura 10. Análisis de la tercera malla al aplicar LKV.

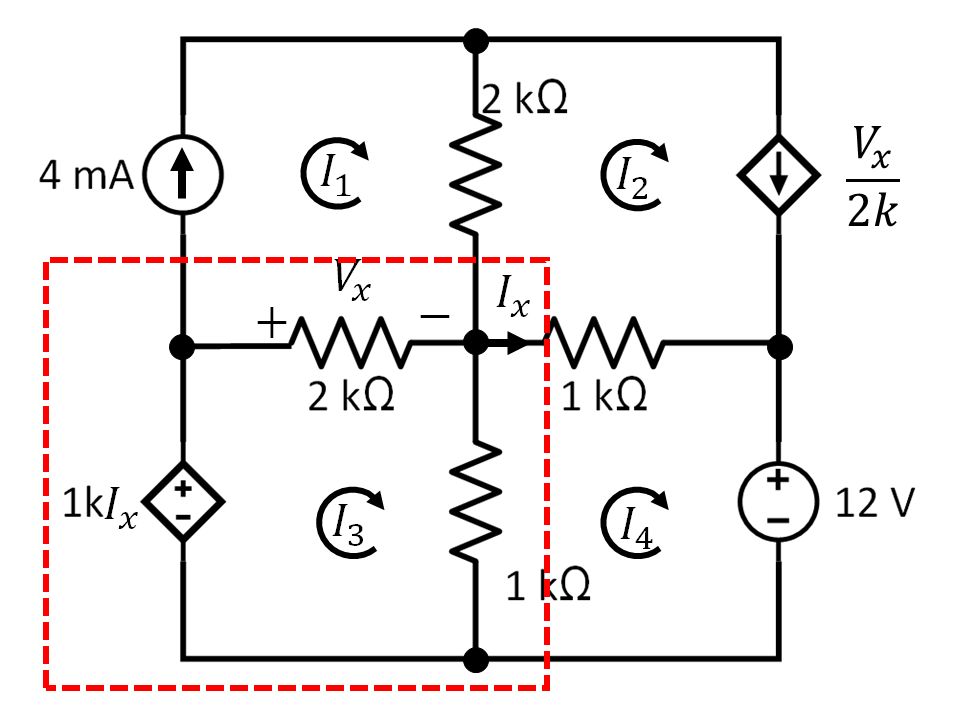
Lo mismo ocurre en la cuarta malla

$\displaystyle \sum_{j=1}^n{V_j} = 0$

$\displaystyle (1 \ \text{k}) (I_4 - I_3) + (1 \ \text{k})(I_4 - I_2) + 12 = 0$

$\displaystyle (1 \ \text{k}) I_4 - (1 \ \text{k}) I_3 + (1 \ \text{k}) I_4 - (1 \ \text{k}) I_2 + 12 = 0$

$\displaystyle - (1 \ \text{k}) I_2 - (1 \ \text{k}) I_3 + (2 \ \text{k}) I_4 + 12 = 0$

$\displaystyle - (1 \ \text{k}) I_2 - (1 \ \text{k}) I_3 + (2 \ \text{k}) I_4 = - 12$

*Figura 11. Análisis de la cuarta malla al aplicar LKV.*

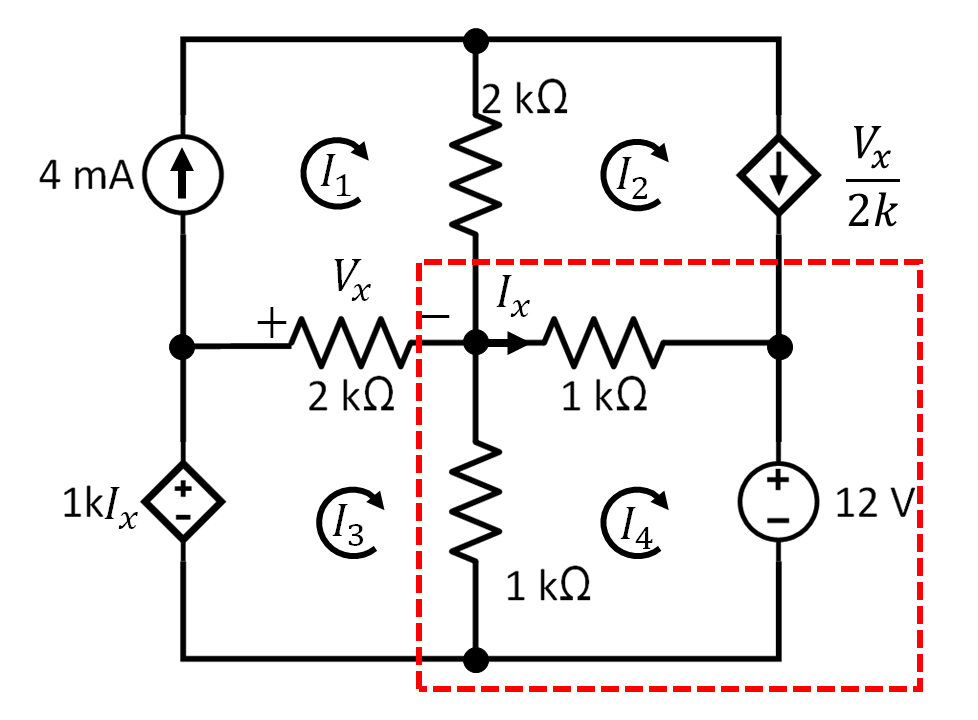
Así que las ecuaciones obtenidas en cada malla son (expresándolo en un sistema de ecuaciones)

Este sistema se puede mostrar en forma matricial

$\displaystyle \left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 1 & 1 & -1 & 0 \\ 0 & 1 \ \text{k} & 3 \ \text{k} & -2 \ \text{k} \\ 0 & - 1 \ \text{k} & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right] \left[ \begin{matrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{matrix} \right] = \left[ \begin{matrix} \frac{4}{\text{k}} \\ 0 \\ 8 \\ -12 \end{matrix} \right]$

Que es similar a su forma general

$\displaystyle \bold{R} \bold{I} = \bold{V}$

Despejando $\bold{I}$ ,

$\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}$

Por lo que es necesario encontrar la inversa de $\bold{R}$ . Para encontrarlo primero se determina su determinante.

$\displaystyle \text{det} \ \bold{R} = \left| \begin{matrix} 1 & 0 & 0 & 0 \\ 1 & 1 & -1 & 0 \\ 0 & 1 \ \text{k} & 3 \ \text{k} & -2 \ \text{k} \\ 0 & - 1 \ \text{k} & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right|$

$\displaystyle \text{det} \ \bold{R} = 4 \ \text{k}^2$

La matriz adjunta de $\bold{R}$ es

$\displaystyle Adj \ \bold{R} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} & C_{14}\\ C_{21} & C_{22} & C_{23} & C_{24}\\ C_{31} & C_{32} & C_{33} & C_{34} \\ C_{41} & C_{42} & C_{43} & C_{44} \end{matrix} \right]$

donde $C_{ij}$ es el cofactor correspondiente y se calcula utilizando la fórmula

$\displaystyle C_{ij} = {(-1)}^{i+j} \ M_{ij}$

donde $M_{ij}$ es el menor del elemento $R_{ij}$ y para encontrar el valor de cada menor, se realiza lo siguiente

$\displaystyle M_{11} = \left|\begin{matrix} 1 & -1 & 0 \\ 1 \ \text{k} & 3 \ \text{k} & -2 \ \text{k} \\ - 1 \ \text{k} & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = 4 \ \text{k}^2$

$\displaystyle M_{12} = \left|\begin{matrix} 1 & -1 & 0 \\ 0 & 3 \ \text{k} & -2 \ \text{k} \\ 0 & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = 4 \ \text{k}^2$

$\displaystyle M_{13} = \left|\begin{matrix} 1 & 1 & 0 \\ 0 & 1 \ \text{k} & -2 \ \text{k} \\ 0 & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = 0$

$\displaystyle M_{14} = \left|\begin{matrix} 1 & 1 & -1 \\ 0 & 1 \ \text{k} & 3 \ \text{k} \\ 0 & - 1 \ \text{k} & - 1 \ \text{k} \end{matrix} \right| = 2 \ \text{k}^2$

$\displaystyle M_{21} = \left|\begin{matrix} 0 & 0 & 0 \\ 1 \ \text{k} & 3 \ \text{k} & -2 \ \text{k} \\ - 1 \ \text{k} & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = 0$

$\displaystyle M_{22} = \left|\begin{matrix} 1 & 0 & 0 \\ 0 & 3 \ \text{k} & -2 \ \text{k} \\ 0 & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = 4 \ \text{k}^2$

$\displaystyle M_{23} = \left|\begin{matrix} 1 & 0 & 0 \\ 0 & 1 \ \text{k} & -2 \ \text{k} \\ 0 & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = 0$

$\displaystyle M_{24} = \left|\begin{matrix} 1 & 0 & 0 \\ 0 & 1 \ \text{k} & 3 \ \text{k} \\ 0 & - 1 \ \text{k} & - 1 \ \text{k} \end{matrix} \right| = 2 \ \text{k}^2$

$\displaystyle M_{31} = \left|\begin{matrix} 0 & 0 & 0 \\ 1 & -1 & 0 \\ - 1 \ \text{k} & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = 0$

$\displaystyle M_{32} = \left|\begin{matrix} 1 & 0 & 0 \\ 1 & -1 & 0 \\ 0 & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = - 2 \ \text{k}$

$\displaystyle M_{33} = \left|\begin{matrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & - 1 \ \text{k} & 2 \ \text{k} \end{matrix} \right| = 2 \ \text{k}$

$\displaystyle M_{34} = \left|\begin{matrix} 1 & 0 & 0 \\ 1 & 1 & -1\\ 0 & - 1 \ \text{k} & - 1 \ \text{k} \end{matrix} \right| = - 2 \ \text{k}$

$\displaystyle M_{41} = \left| \begin{matrix} 0 & 0 & 0 \\ 1 & -1 & 0 \\ 1 \ \text{k} & 3 \ \text{k} & -2 \ \text{k} \end{matrix} \right| = 0$

$\displaystyle M_{42} = \left|\begin{matrix} 1 & 0 & 0 \\ 1 & -1 & 0 \\ 0 & 3 \ \text{k} & -2 \ \text{k} \end{matrix} \right| = 2 \ \text{k}$

$\displaystyle M_{43} = \left|\begin{matrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 1 \ \text{k} & -2 \ \text{k} \end{matrix} \right| = - 2 \ \text{k}$

$\displaystyle M_{44} = \left|\begin{matrix} 1 & 0 & 0 \\ 1 & 1 & -1\\ 0 & 1 \ \text{k} & 3 \ \text{k} \end{matrix} \right| = 4 \ \text{k}$

Calculando cada cofactor, se tienen los siguientes resultados

\displaystyle C_{11} = M_{11} = 4 \ \text{k}^2

\displaystyle C_{12} = -M_{12} = - 4 \ \text{k}^2

Así, la matriz adjunta es

$\displaystyle Adj \ \bold{R} = \left[\begin{matrix} 4 \ \text{k}^2 & -4 \ \text{k}^2 & 0 & -2 \ \text{k}^2\\ 0 & 4 \ \text{k}^2 & 0 & 2 \ \text{k}^2 \\ 0 & 2 \ \text{k} & 2 \ \text{k} & 2 \ \text{k} \\ 0 & 2 \ \text{k} & 2 \ \text{k} & 4 \ \text{k} \end{matrix} \right]$

y la matriz adjunta traspuesta de $\bold{R}$ es

$\displaystyle {(Adj \ \bold{R})}^T = \left[\begin{matrix} 4 \ \text{k}^2 & 0 & 0 & 0 \\ -4 \ \text{k}^2 & 4 \ \text{k}^2 & 2 \ \text{k} & 2 \ \text{k} \\ 0 & 0 & 2 \ \text{k} & 2 \ \text{k} \\ -2 \ \text{k}^2 & 2 \ \text{k}^2 & 2 \ \text{k} & 4 \ \text{k} \end{matrix} \right]$

Entonces, la matriz inversa de $\bold{R}$ es

$\displaystyle \bold{R}^{-1} = \frac{{\left(Adj \ \bold{R}\right)}^T}{\text{det} \ \bold{R}} = \left(\frac{1}{\text{det} \ \bold{R}} \right) {\left(Adj \ \bold{R}\right)}^T$

$\displaystyle \bold{R}^{-1} = \left(\frac{1}{4 \ \text{k}^2} \right) \left[\begin{matrix} 4 \ \text{k}^2 & 0 & 0 & 0 \\ -4 \ \text{k}^2 & 4 \ \text{k}^2 & 2 \ \text{k} & 2 \ \text{k} \\ 0 & 0 & 2 \ \text{k} & 2 \ \text{k} \\ -2 \ \text{k}^2 & 2 \ \text{k}^2 & 2 \ \text{k} & 4 \ \text{k} \end{matrix} \right]$

$\displaystyle \bold{R}^{-1} = \left[\begin{matrix} \left(\frac{1}{4 \ \text{k}^2} \right)(4 \ \text{k}^2) & \left(\frac{1}{4 \ \text{k}^2} \right)(0) & \left(\frac{1}{4 \ \text{k}^2} \right)(0) & \left(\frac{1}{4 \ \text{k}^2} \right)(0) \\ \\ \left(\frac{1}{4 \ \text{k}^2} \right)(-4 \ \text{k}^2) & \left(\frac{1}{4 \ \text{k}^2} \right)(4 \ \text{k}^2) & \left(\frac{1}{4 \ \text{k}^2} \right)(2 \ \text{k}) & \left(\frac{1}{4 \ \text{k}^2} \right)(2 \ \text{k}) \\ \\ \left(\frac{1}{4 \ \text{k}^2} \right)(0) & \left(\frac{1}{4 \ \text{k}^2} \right)(0) & \left(\frac{1}{4 \ \text{k}^2} \right)(2 \ \text{k}) & \left(\frac{1}{4 \ \text{k}^2} \right)(2 \ \text{k}) \\ \\ \left(\frac{1}{4 \ \text{k}^2} \right)(-2 \ \text{k}^2) & \left(\frac{1}{4 \ \text{k}^2} \right)(2 \ \text{k}^2) & \left(\frac{1}{4 \ \text{k}^2} \right)(2 \ \text{k}) & \left(\frac{1}{4 \ \text{k}^2} \right)(4 \ \text{k}) \end{matrix} \right]$

$\displaystyle \bold{R}^{-1} = \left[\begin{matrix} 1 & 0 & 0 & 0 \\ \\ - 1 & 1 & \frac{1}{2 \ \text{k}} & \frac{1}{2 \ \text{k}} \\ \\ 0 & 0 & \frac{1}{2 \ \text{k}} & \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{2} & \frac{1}{2} & \frac{1}{2 \ \text{k}} & \frac{1}{1 \ \text{k}} \end{matrix} \right]$

Regresando al último despeje matricial y sustituyendo

$\displaystyle \bold{I} = \bold{R}^{-1} \bold{V}$

$\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{matrix} \right] = \left[\begin{matrix} 1 & 0 & 0 & 0 \\ \\ - 1 & 1 & \frac{1}{2 \ \text{k}} & \frac{1}{2 \ \text{k}} \\ \\ 0 & 0 & \frac{1}{2 \ \text{k}} & \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{2} & \frac{1}{2} & \frac{1}{2 \ \text{k}} & \frac{1}{1 \ \text{k}} \end{matrix} \right] \left[\begin{matrix} \frac{4}{\text{k}} \\ \\ 0 \\ \\ 8 \\ \\ - 12 \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{matrix} \right] = \left[\begin{matrix} (1) \left(\frac{4}{\text{k}} \right) + (0)(0) + (0)(8) + (0)(-12) \\ \\ (- 1) \left( \frac{4}{\text{k}} \right) + (1)(0) + \left(\frac{1}{2 \ \text{k}} \right)(8) + \left(\frac{1}{2 \ \text{k}} \right)(-12) \\ \\ (0)\left( \frac{4}{\text{k}} \right) + (0) (0) + \left(\frac{1}{2 \ \text{k}} \right)(8) + \left(\frac{1}{2 \ \text{k}} \right) (-12) \\ \\ \left(- \frac{1}{2} \right)\left( \frac{4}{\text{k}} \right) + \left(\frac{1}{2} \right)(0) + \left(\frac{1}{2 \ \text{k}} \right)(8) + \left(\frac{1}{\text{k}} \right)(-12) \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{matrix} \right] = \left[\begin{matrix} \frac{4}{\text{k}} + 0 + 0 + 0 \\ \\ - \frac{4}{\text{k}} + 0 + \frac{8}{2 \ \text{k}} - \frac{12}{2 \ \text{k}} \\ \\ 0 + 0 + \frac{8}{2 \ \text{k}} - \frac{12}{2 \ \text{k}} \\ \\ - \frac{4}{2 \ \text{k}} + 0 + \frac{8}{2 \ \text{k}} - \frac{12}{\text{k}} \end{matrix} \right] = \left[\begin{matrix} \frac{4}{\text{k}} \\ \\ - \frac{4}{\text{k}} + \frac{4}{\text{k}} - \frac{6}{\text{k}} \\ \\ \frac{4}{\text{k}} - \frac{6}{\text{k}} \\ \\ - \frac{2}{\text{k}} + \frac{4}{\text{k}} - \frac{12}{\text{k}} \end{matrix} \right]$

$\displaystyle \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{matrix} \right] = \left[\begin{matrix} \frac{4}{\text{k}} \\ \\ - \frac{6}{\text{k}} \\ \\ - \frac{2}{\text{k}} \\ \\ - \frac{10}{\text{k}} \end{matrix} \right] = \left[\begin{matrix} \frac{4}{1 \times 10^{3}} \\ \\ - \frac{6}{1 \times 10^{3}} \\ \\ - \frac{2}{1 \times 10^{3}} \\ \\ - \frac{10}{1 \times 10^{3}} \end{matrix} \right] = \left[\begin{matrix} 4 \times 10^{-3} \\ \\ - 6 \times 10^{-3} \\ \\ - 2 \times 10^{-3} \\ \\ - 10 \times 10^{-3} \end{matrix} \right] = \left[\begin{matrix} 4 \\ \\ - 6 \\ \\ - 2 \\ \\ - 10 \end{matrix} \right] \times 10^{-3}$

$\displaystyle \therefore \left[\begin{matrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{matrix} \right] = \left[\begin{matrix} 4 \\ \\ - 6 \\ \\ - 2 \\ \\ - 10 \end{matrix} \right] \ \text{mA}$

Finalmente, los valores de las corrientes de cada malla son $I_1 = 4 \ \text{mA}$ , $I_2 = -6 \ \text{mA}$ , $I_3 = -2 \ \text{mA}$ y $I_4 = -10 \ \text{mA}$ .

$\displaystyle C_{11} = {(-1)}^{1+1} \left(8 \ \text{k} \right) = 8 \ \text{k}$	$\displaystyle C_{12} = {(-1)}^{1+2} \left(- 6 \ \text{k} \right) = 6 \ \text{k}$
$\displaystyle C_{21} = {(-1)}^{2+1} \left(2 \ \text{k} \right) = - 2 \ \text{k}$	$\displaystyle C_{22} = {(-1)}^{2+2} \left(-2 \ \text{k} \right) = -2 \ \text{k}$

$\displaystyle C_{11} = M_{11} = 4 \ \text{k}^2$	$\displaystyle C_{12} = -M_{12} = - 4 \ \text{k}^2$	$\displaystyle C_{13} = M_{13} = 0$	$\displaystyle C_{14} = - M_{14} = - 2 \ \text{k}^2$
$\displaystyle C_{21} =- M_{21} = 0$	$\displaystyle C_{22} = M_{22} = 4 \ \text{k}^2$	$\displaystyle C_{23} = - M_{23} = 0$	$\displaystyle C_{24} = M_{24} = 2 \ \text{k}^2$
$\displaystyle C_{31} = M_{31} = 0$	$\displaystyle C_{32} = - M_{32} = 2 \ \text{k}$	$\displaystyle C_{33} = M_{33} = 2 \ \text{k}$	$\displaystyle C_{34} = - M_{34} = 2 \ \text{k}$
$\displaystyle C_{41} = - M_{41} = 0$	$\displaystyle C_{42} = M_{42} = 2 \ \text{k}$	$\displaystyle C_{43} = - M_{43} = 2\ \text{k}$	$\displaystyle C_{44} = M_{44} = 4 \ \text{k}$

Análisis de lazos para circuitos con fuentes dependientes. Circuitos eléctricos.

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Análisis de lazos para circuitos con fuentes dependientes. Circuitos eléctricos.

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta