Introducción
La refracción de la luz es un fenómeno óptico que consiste en la desviación que sufre un rayo luminoso al pasar de un medio a otro con diferente densidad, y tiene como consecuencia un cambio de velocidad, la cual se recupera al regresar nuevamente al medio original. Por ejemplo, la desviación que experimenta un rayo de luz al incidir sobre el agua: cualquier objeto recto, como un lápiz o popote dentro del agua, dan la impresión de estar quebrados. Se debe a que o que se observa realmente no es la parte sumergida, sino su imagen virtual situada arriba de la posición real del objeto.



Figura 1. Actividades donde se presenta refracción.
Por la refracción, una moneda en el fondo de un recipiente de la impresión de estar más elevada, debido a que los rayos refractados constituyen un haz divergente, así que llegan al ojo como si hubiesen sido emitidos desde el punto de la imagen virtual (superior). También este fenómeno, una alberca con aguas tranquilas le parece menos profunda a una persona sentada en la orilla, porque la refracción de la luz no permite ver el fondo, sino más bien su imagen en una posición más elevada. Pasa algo similar con la luz de una estrella, que al penetrar a la atmósfera encuentra capas de aire cada vez más densas y por consiguiente, índices de refracción cada vez mayores, por lo que sufre refracciones sucesivas y el observador en tierra percibe la imagen virtual, no la real.
La refracción también se presenta con la luz del Sol al final del día, que aun cuando éste se encuentra ya por debajo de la línea del horizonte se sigue observando. También debido a la refracción, cuando un rayo de luz blanca atraviesa un prisma, se genera una desviación y dispersión que la separa en los colores que la forman. Lo mismo sucede con el arco iris, que se origina cuando la luz blanca incide sobre gotas de lluvia. El fenómeno de refracción se rige por primera y la segunda ley de la refracción.
Primera ley de la refracción
La primera ley de la refracción establece que el rayo incidente, el rayo refractado, así como la normal, se encuentran en un mismo plano (forma un sistema coplanar). Cuando el ángulo de refracción es menor que el de incidencia, el rayo refractado se acerca a la normal, debido a que pasa a un medio de mayor densidad, como sucede cuando el aire incide en vidrio, y se aleja cuando ocurre lo contrario, esto es, al pasar de un medio de mayor a uno de menor densidad, como cuando la luz deja el vidrio para entrar en el aire.
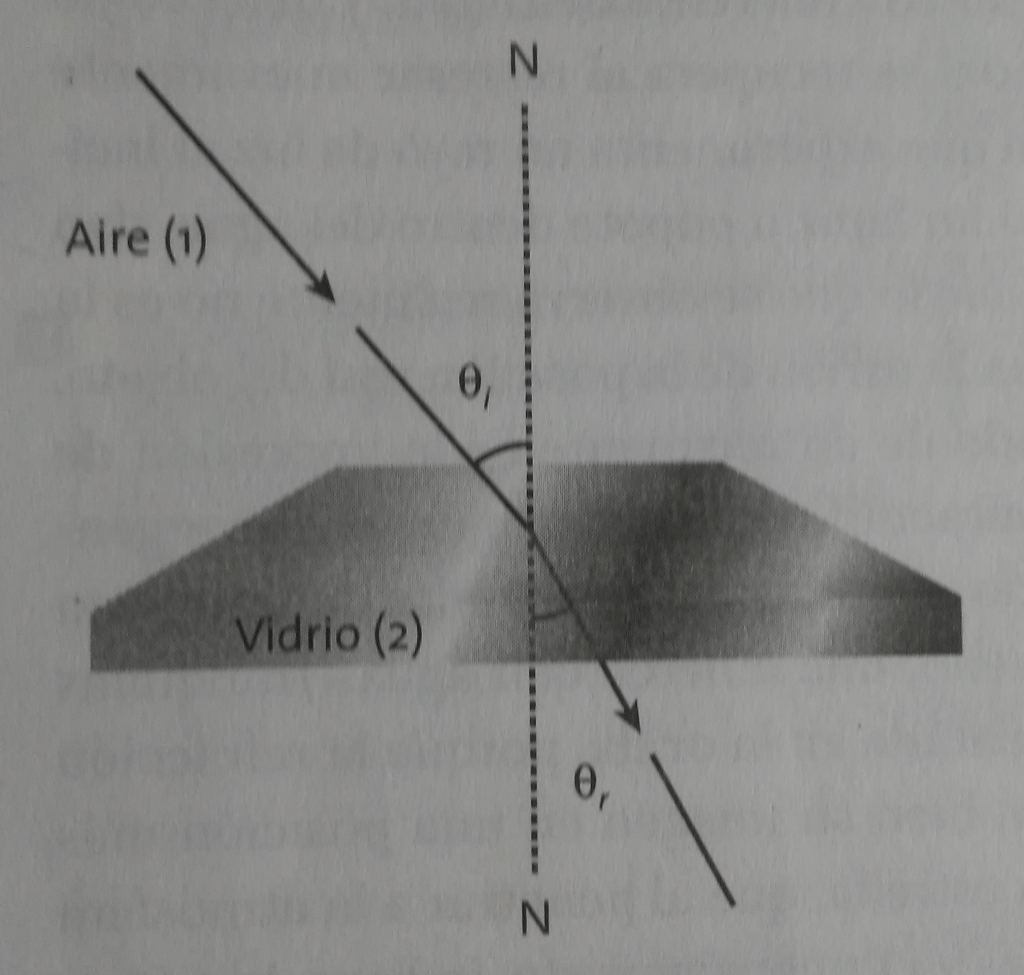
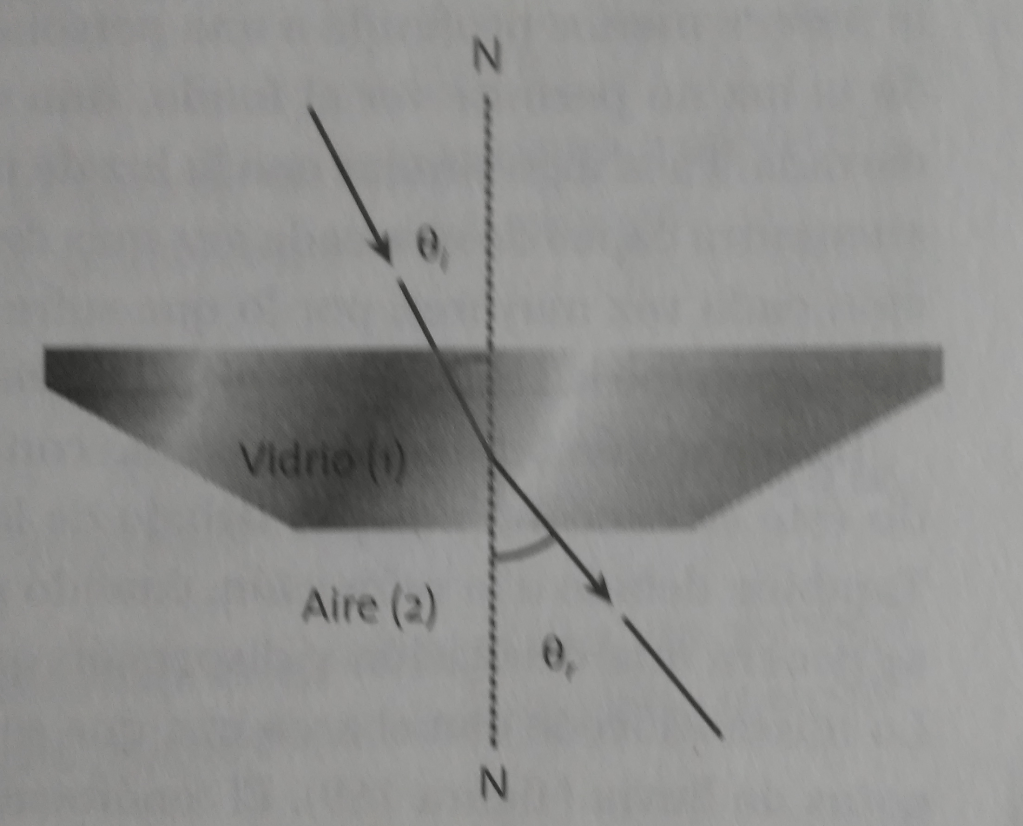
Segunda ley de la refracción
La segunda ley de la refracción, conocida como ley de Snell – Willebrord Snell (1591-1626), físico, matemático y astrónomo holandés que hizo estudios sobre la refracción de la luz – establece que para cada par de sustancias transparentes, la relación entre el seno del ángulo de incidencia y el ángulo de refracción es constante. A este número se le llama índice de refracción. También definido como la relación entre la velocidad de la luz en el vacío y la que presenta en un determinado medio, su valor siempre será mayor a la unidad y es adimensional, es decir, no tiene unidades.
En general, se considera que la velocidad de la luz en el vacío es prácticamente igual a la que se presenta en el aire.
Indice de refracción de sustancias
| Sustancia | Índice de refracción |
| Agua | 1.33 |
| Vidrio | 1.5 |
Velocidad de la luz en diversos medios
| Sustancia | Velocidad de la luz (km/s) |
| Vacío | 300 000 |
| Agua | 225 000 |
El índice de refracción se utiliza para conocer el grado de desviación que experimentan los rayos de luz al pasar a través de lentes de anteojos, binoculares y cámaras que forman la imagen en la posición y el lugar correctos. Como el índice de refracción es constante para una sustancia homogénea, constituye una propiedad física definida con la cual puede detectarse, por ejemplo, si un producto determinado no es puro, sino una mezcla de, digamos, mantequilla y margarina. Las ecuaciones que permiten su cálculo son
Donde
es el índice de refracción, es adimensional (sin unidades).
es el ángulo de incidencia, en grados (°).
es el ángulo de refracción, en grados (°).
Donde
es el índice de refracción, es adimensional (sin unidades).
es la velocidad del medio 1, en metros por segundo (m/s).
es la velocidad del medio 2, en metros por segundo (m/s).
Problemas resueltos
Problema 1. Si las velocidades en aire y agua son 300 000 (km/s) y 225 000 (km/s), respectivamente, ¿qué índice de refracción presenta el rayo de luz al incidir en el agua?
Solución. Se tiene el siguiente esquema
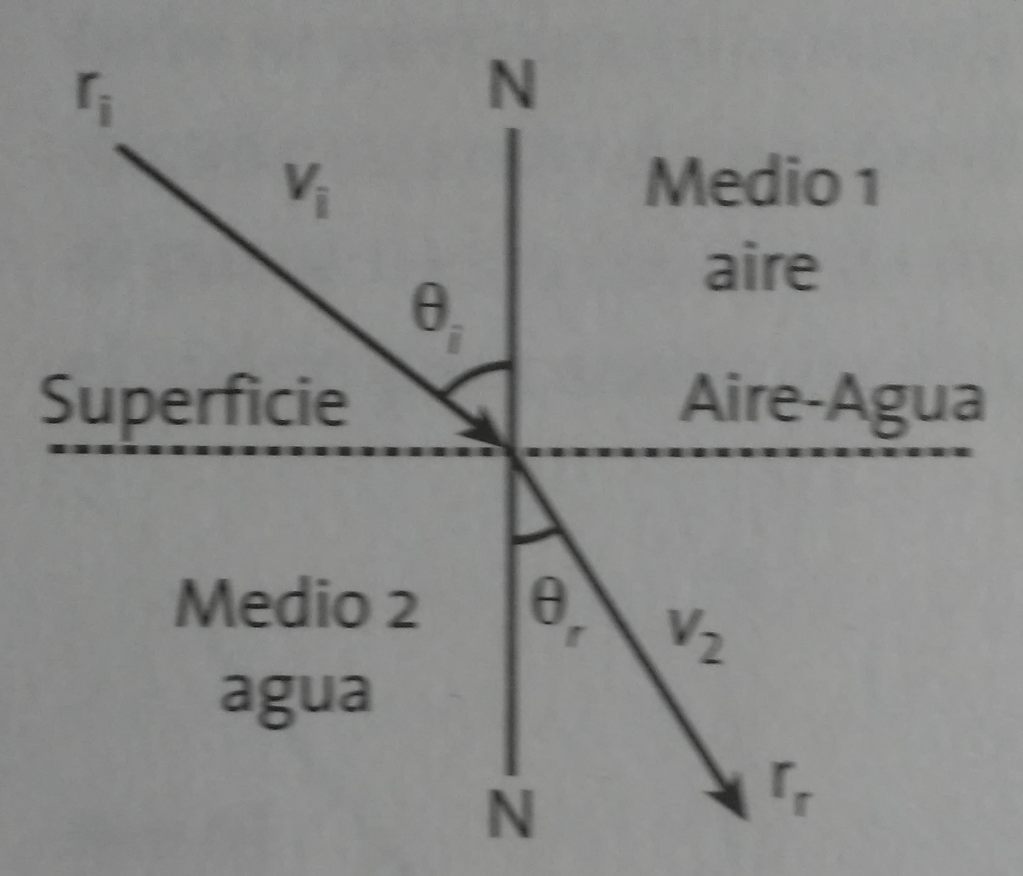
Tomando la fórmula del índice de refracción donde toma en cuenta las velocidades
Sustituyendo
Problema 2. Un rayo luminoso que viaja en el aire atraviesa un vidrio refractándose 35° respecto a la normal. Si se presenta un índice de refracción de 1.5, ¿con qué ángulo de incidencia lo hace?
Solución. El esquema es el siguiente
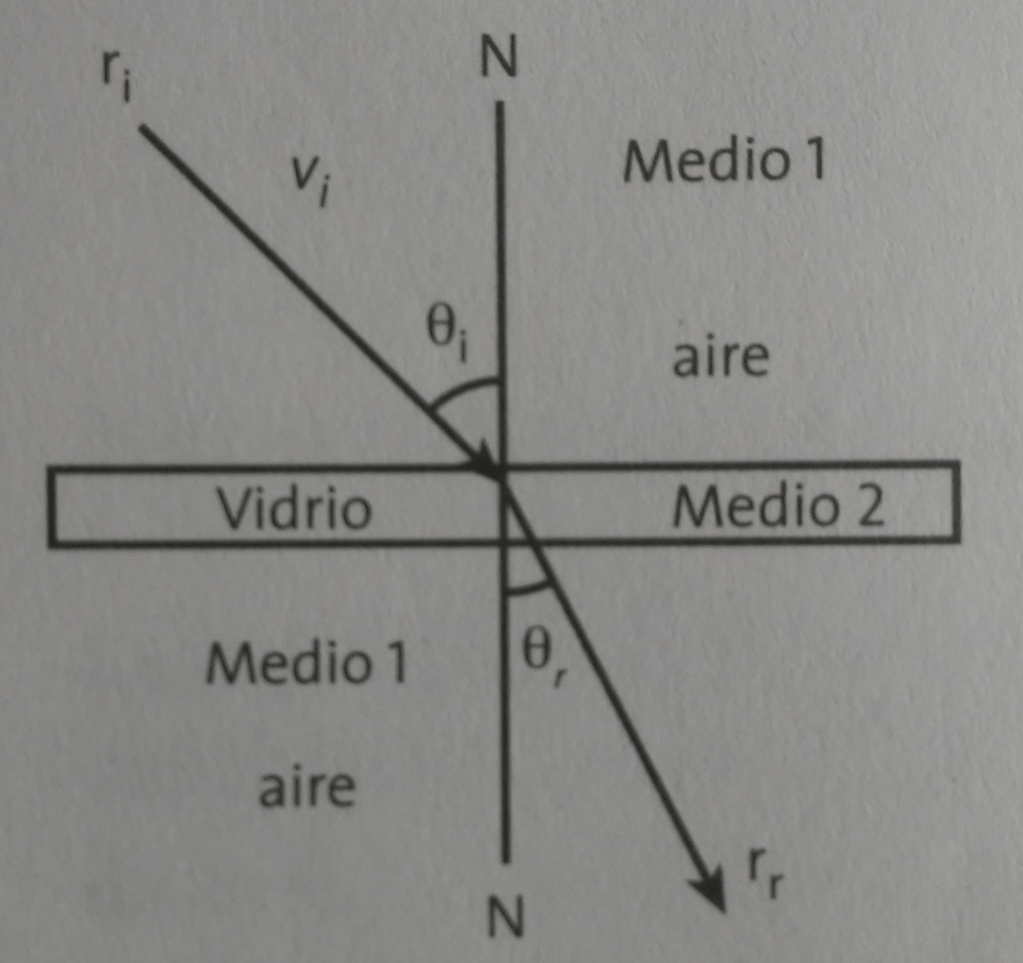
Tomando la fórmula del índice de refracción donde toma en cuenta los ángulos
Sustituyendo
Despejando
°
thx informasinya yah gan. keren abis
Me gustaMe gusta
Very beautiful article
Me gustaMe gusta
Your place is valueble for me. Thanks!?
Me gustaMe gusta